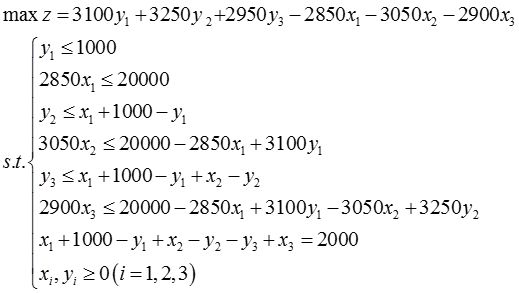1 分别用图解法和单纯形法求解下列线性规划问题:
(1)指出问题具有唯一最优解、无穷多最优解、无界解还是无可行解;
(2)当具有有限最优解时,指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。
(1)
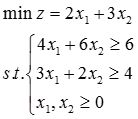
(2)
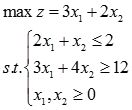
(3)
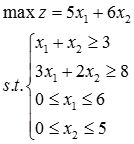
(4)
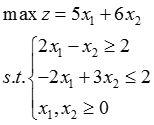
解: (1)图解法:
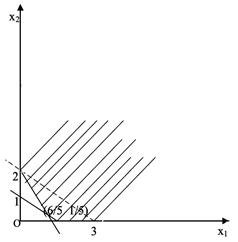
图2-1-1
当
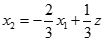 经过点
经过点
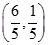 时,z最小,且有无穷多个最优解。
时,z最小,且有无穷多个最优解。
单纯形法:
在上述问题的约束条件中令z ′ =-z,分别加入剩余变量x 3 ,x 4 ,引入人工变量x 5 ,x 6 化为标准型:
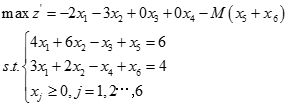
由线性规划问题的标准型可列出单纯初始形表并逐步迭代,计算结果如表2-1-1所示:
表2-1-1
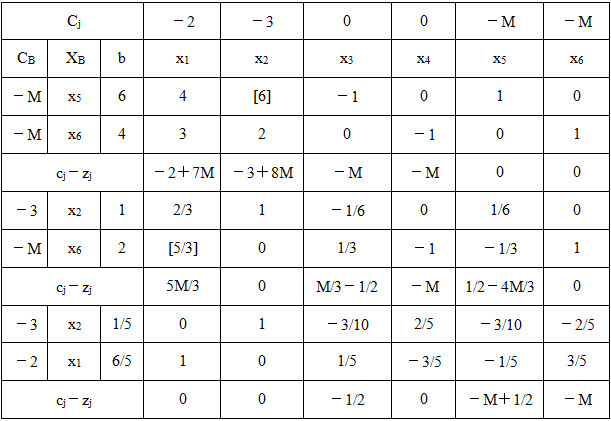
单纯形表的计算结果表明
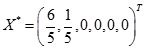 ,同时发现存在非基变量检验数为0,说明该线性规划问题有无穷多最优解。
,同时发现存在非基变量检验数为0,说明该线性规划问题有无穷多最优解。
(2)图解法:
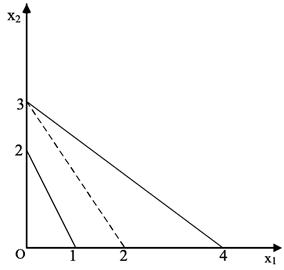
图2-1-2
在x 1 ,x 2 ≥0情况下约束条件无可行域,因此无可行解。
在图解法中已看出本例无可行解,现用单纯形法求解。在添加松弛变量和人工变量后,模型可写成
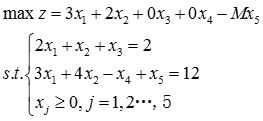
由线性规划问题的标准型可列出单纯初始形表并逐步迭代,计算结果如表2-1-2所示:
表2-1-2
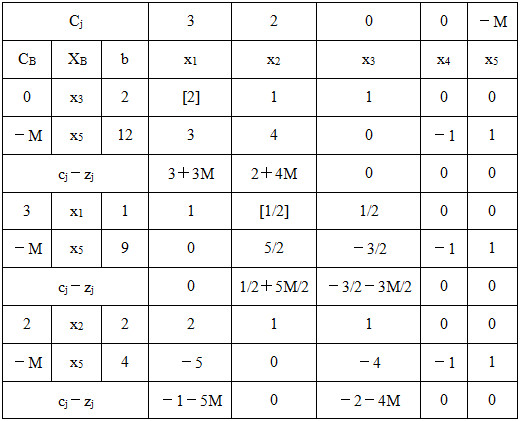
此时所有检验数均≤0,但基变量中仍含有非零的人工变量,表明问题无可行解。
(3)图解法:
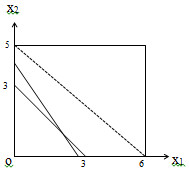
图2-1-3
当
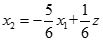 经过点(6,5)时,z最大,且有唯一最优解。
经过点(6,5)时,z最大,且有唯一最优解。
单纯形法:
加入剩余变量x 3 ,x 4 ,引入人工变量x 5 ,x 6 ,加入松弛变量x 7 ,x 8 ,化为标准型如下:
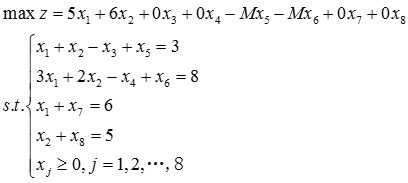
由线性规划问题的标准型可列出单纯初始形表并逐步迭代,计算结果如表2-1-3所示。
表2-1-3
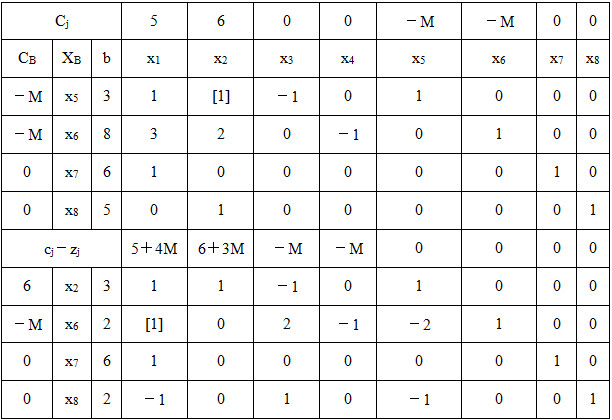
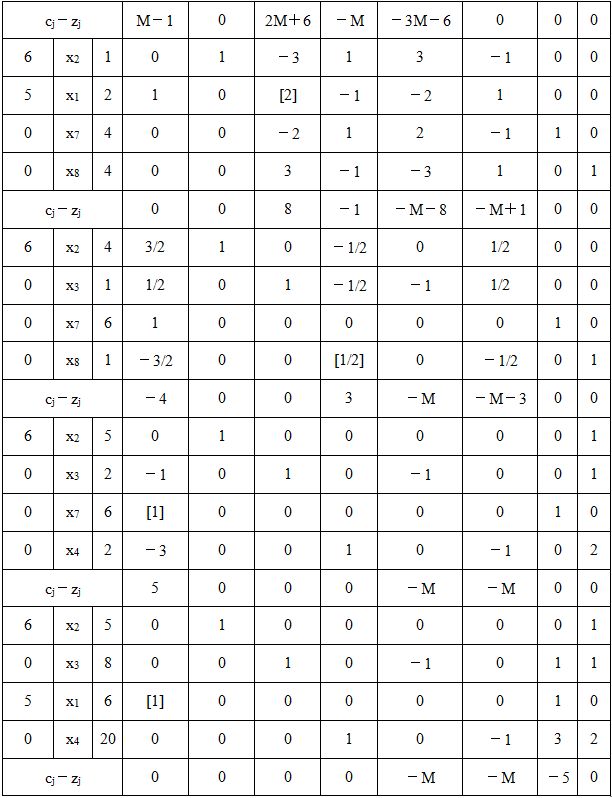
单纯形表计算结果表明X * =(6,5,8,20,0,0,0,0) T ,Z * =60。
(4)图解法求解:该问题的可行域为无界域,如图2-1-4所示。目标函数有无界解。
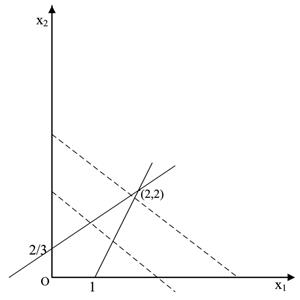
图2-1-4
单纯形法:
加入剩余变量x 3 ,松弛变量x 4 ,引入人工变量x 5 ,化为标准型为:
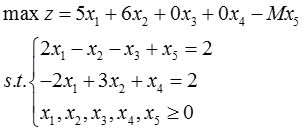
由线性规划问题的标准型可列出单纯初始形表并逐步迭代,计算结果如表2-1-4所示:
表2-1-4
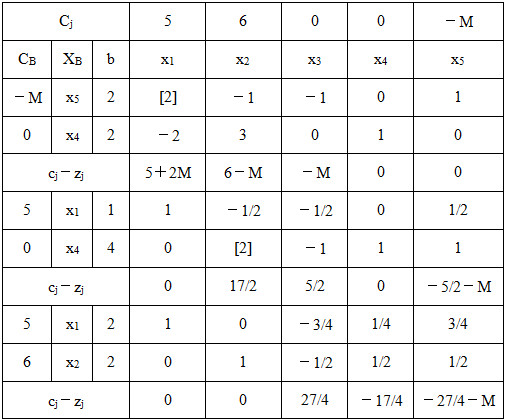
发现存在x 3 检验数>0,且这对应列向量均为负数,根据解的判别规则,说明线性规划有无界解。
2 将下述线性规划问题化成标准形式。
(1)
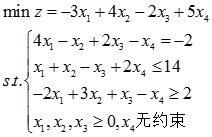
(2)
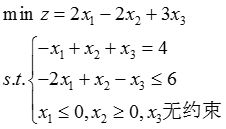
解: (1)化成标准形式:
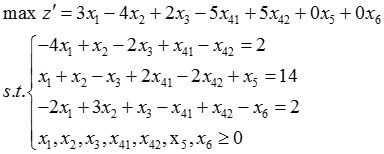
(2)化成标准形式:
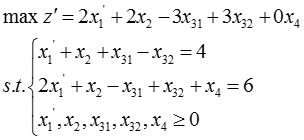
3 对下述线性规划问题找出所有基解,指出哪些是基可行解,并确定最优解。
(1)
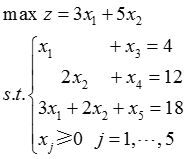
(2)
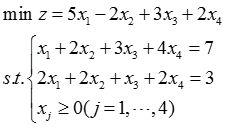
解: (1)由于约束方程组为3×5阶系数矩阵,其秩为3,其基变量可任取约束方程组中的三列,取非基变量的值为0,此时求出的基变量的值为方程的一个基解,有一个基就可以求出一个基解。设X i (i=1,2,3,…,8)是对应约束方程组的基变量,可知
X 1 =(x 3 ,x 4 ,x 5 ),令x 1 =0,x 2 =0,可求出x 3 =4,x 4 =12,x 5 =18
X 2 =(x 1 ,x 4 ,x 5 ),令x 3 =0,x 2 =0,可求出x 1 =4,x 4 =12,x 5 =6
X 3 =(x 1 ,x 3 ,x 4 ),令x 2 =0,x 5 =0,可求出x 1 =6,x 3 =-2,x 4 =12
X 4 =(x 1 ,x 2 ,x 4 ),令x 3 =0,x 5 =0,可求出x 1 =4,x 2 =3,x 4 =6
X 5 =(x 2 ,x 3 ,x 5 ),令x 1 =0,x 4 =0,可求出x 2 =6,x 3 =4,x 5 =6
X 6 =(x 1 ,x 2 ,x 3 ),令x 4 =0,x 5 =0,可求出x 1 =2,x 2 =6,x 3 =2
X 7 =(x 1 ,x 2 ,x 5 ),令x 3 =0,x 4 =0,可求出x 1 =4,x 2 =6,x 5 =-6
X 8 =(x 2 ,x 3 ,x 4 ),令x 1 =0,x 5 =0,可求出x 2 =9,x 3 =4,x 4 =-6
将每一个基解代入目标函数中,求出每一个对应的z值,满足约束条件x i ≥0的解为基可行解,所有基可行解中满足z值最大的解为最优解。最终计算如表2-1-5所示,其中□标示的为基可行解,*标示的为最优解。
表2-1-5
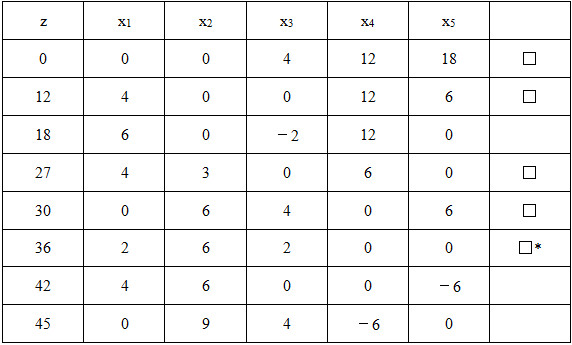
故可得方程的最优解为x 1 =2,x 2 =6,x 3 =2,x 4 =0,x 5 =0,z * =36
(2)该线性规划问题的标准形式为:
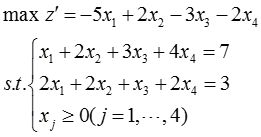
其全部基解见表2-1-6中的 ① ~ ⑥ ,□标示的为基可行解,*标示的为最优解,z * =5。
表2-1-6
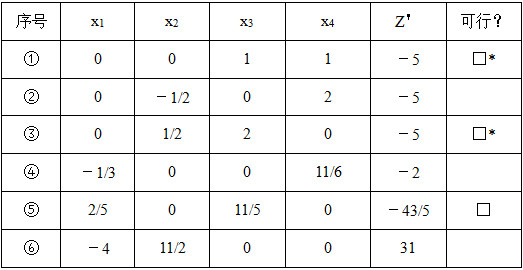
4 题1(3)中,若目标函数变为max z=cx 1 +dx 2 ,讨论c,d的值如何变化,使该问题可行域的每个顶点依次使目标函数达到最优。
解:
有目标函数max z=cx
1
+dx
2
可得:
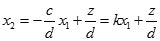 ,其中
,其中
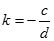 。
。
(1)当k≤0时
若c≥0,d>0,可行域的顶点(6,5)使目标函数达到最优;
若c≤0,d<0,-3/2≤k≤-1,可行域的顶点(2,1)使目标函数达到最优;
若c≤0,d<0,k≤-3/2,可行域的顶点(0,4)使目标函数达到最优。
(2)当k≥0时
若c≥0,d<0,可行域的顶点(6,0)使目标函数达到最优;
若c≤0,d>0,可行域的顶点(0,5)使目标函数达到最优。
(3)当k不存在时
即d=0时,若c≥0,可行域的边界x 1 =6使目标函数达到最优;
若c≤0,可行域的边界x 1 =0使目标函数达到最优。
5 考虑下述线性规划问题:
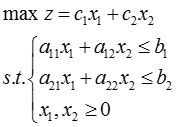
式中,1≤c 1 ≤3,4≤c 2 ≤6,-1≤a 11 ≤3,2≤a 12 ≤5,8≤b 1 ≤12,2≤a 21 ≤5,4≤a 22 ≤6,10≤b 2 ≤14,试确定目标函数最优值的下界和上界。
解: 上界对应的模型如下(c,b取大,a取小)
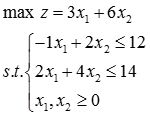
最优值(上界)为:21。
下界对应的模型如下(c,b取小,a取大)
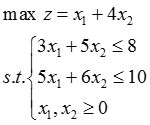
最优值(下界)为6.4。
6 分别用单纯形法中的大M法和两阶段法求解下列线性规划问题,并指出属哪一类解。
(1)
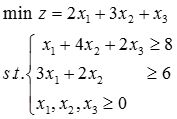
(2)
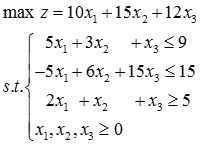
解: (1)大M法:
在上述线性规划问题的约束条件中减去剩余变量x 4 、x 5 ,再分别加上人工变量x 6 、x 7 ,得
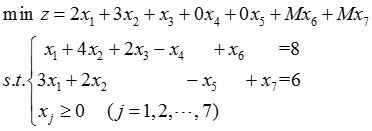
其中M是一个任意大的正数,据此可列出初始单纯形表如表2-1-7所示。
表2-1-7
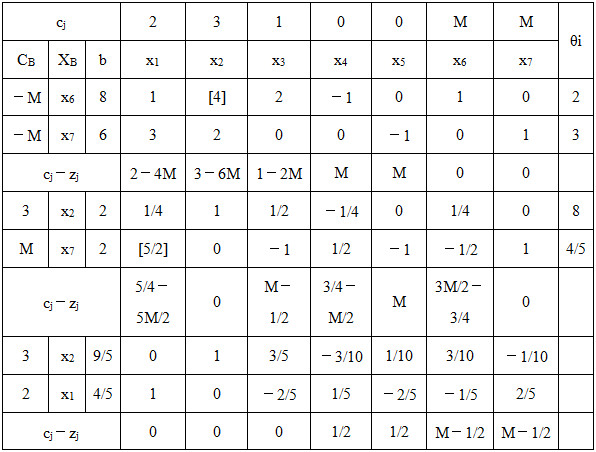
由单纯形表的计算结果得:最优解
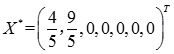
目标函数最优值
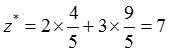
X存在非基变量检验数σ 3 =0,故该线性规划问题有无穷多最优解。
两阶段法:
先在上述线性规划问题的约束条件中减去剩余变量x 4 、x 5 ,再分别加上人工变量x 6 、x 7 ,得第一阶段的数学模型
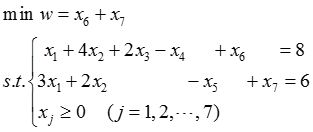
据此可列出单纯初始形表如表2-1-8所示。
表2-1-8
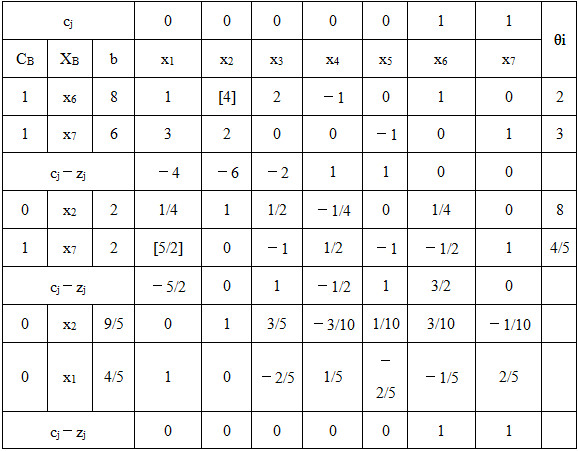
第一阶段求得的最优解
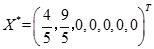 ,目标函数的最优值w
*
=0,因人工变量x
6
=x
7
=0,所以
,目标函数的最优值w
*
=0,因人工变量x
6
=x
7
=0,所以
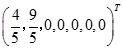 是原线性规划问题的基可行解。于是可以进行第二阶段计算,将第一阶段的最终表中的人工变量取消,并填入原问题的目标函数的系数,如表2-1-9所示。
是原线性规划问题的基可行解。于是可以进行第二阶段计算,将第一阶段的最终表中的人工变量取消,并填入原问题的目标函数的系数,如表2-1-9所示。
表2-1-9
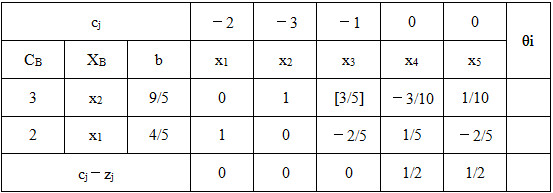
由表中计算可知,原线性规划问题的最优解
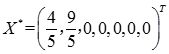 ,目标函数的最优值
,目标函数的最优值
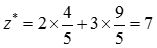 ,由于存在非基变量检验数σ
3
=0,故该线性规划问题有无穷多最优解。
,由于存在非基变量检验数σ
3
=0,故该线性规划问题有无穷多最优解。
(2)大M法:
在上述线性规划问题的约束条件中加上松弛变量x 4 、x 5 ,再减去剩余变量x 6 ,再加上人工变量x 7 ,得
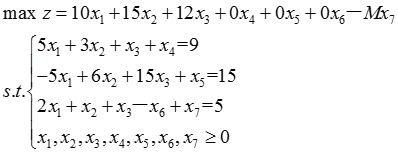
其中M是一个任意大的正数,据此可列出单纯形表如表2-1-10所示。
表2-1-10
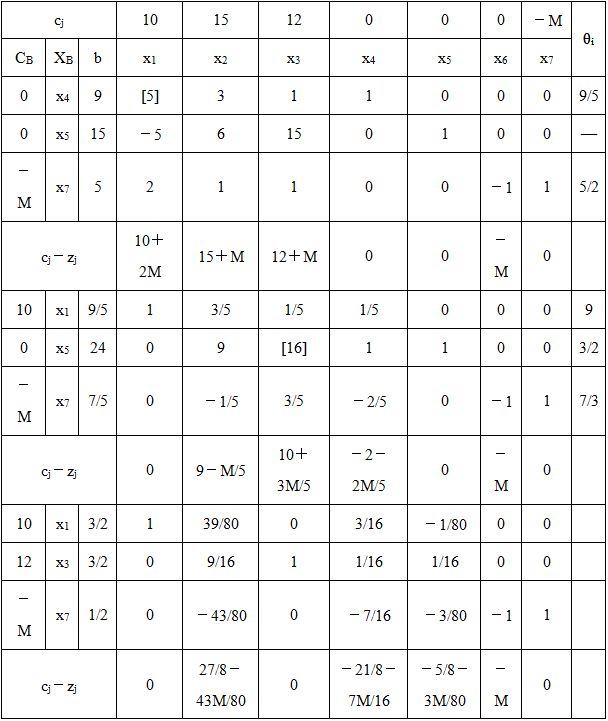
由单纯形表的最终表可以看出,所有非基变量检验数σ j <0,且存在人工变量x 7 =1/2,故原线性规划问题无可行解。
两阶段法:
在上述线性规划问题的约束条件中加上松弛变量x 4 、x 5 ,减去剩余变量x 6 ,再加上人工变量x 7 ,得第一阶段的数学模型
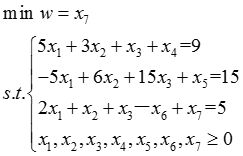
据此可列出单纯形表如表2-1-11所示。
表2-1-11
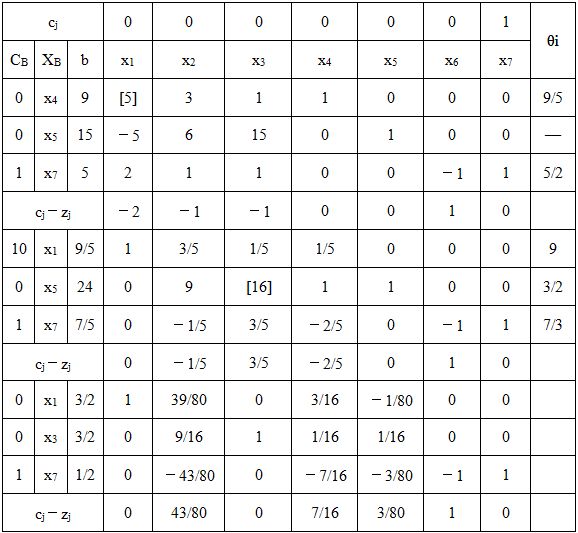
第一阶段求得最优解
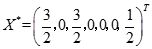 ,因人工变量
,因人工变量
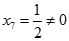 ,且非基变量检验数σ
j
<0,所以原线性规划问题无可行解。
,且非基变量检验数σ
j
<0,所以原线性规划问题无可行解。
7 已知某线性规划问题的初始单纯形表和用单纯形法迭代后得到的表2-1-12,试求括弧中未知数a~l的值。
表2-1-12

解: 由最终单纯形表知,x 1 ,x 5 为基变量,所以g=1,h=0,l=0;由x 4 出基,x 1 入基,所以约束一除2得到新的约束一,所以c=4,d=-2,f=3;反之,得b=2;由新的约束一+约束二得到新的约束二,所以i=5,e=2;同理,等式三减去三倍的新的约束一得到新的等式三,所以a=3,j=5,k=-1.5。
综上,b=2,c=4,d=-2,g=1,h=0,f=3,i=5,e=2,l=0,a=3,j=5,k=-1.5。
8 线性规划问题如下:
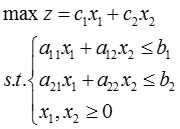
用单纯形法求解得表2-1-13(表中x 3 ,x 4 为松弛变量)
表2-1-13
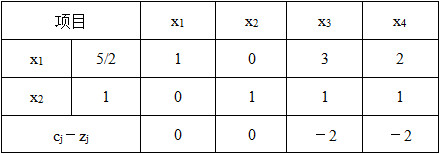
求a 11 ,a 12 ,a 21 ,a 22 ,c 1 ,c 2 ,b 1 ,b 2 的值。
解: 初始单纯形表(见表2-1-14)
表2-1-14
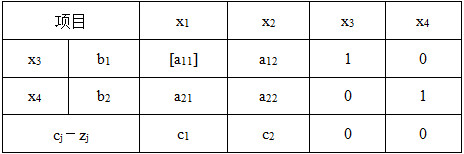
假设第一个进基变量为x 1 ,出基变量为x 3 ,则单纯形表迭代为表2-1-15。
表2-1-15
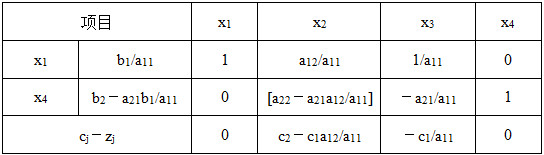
下一步进基变量为x 2 ,出基变量为x 4 ,令m=a 22 -a 21 a 12 /a 11 ,n=c 2 -c 1 a 12 /a 11 ,t=b 2 -a 21 b 1 /(ma 11 )单纯形表迭代为表2-1-16。
表2-1-16
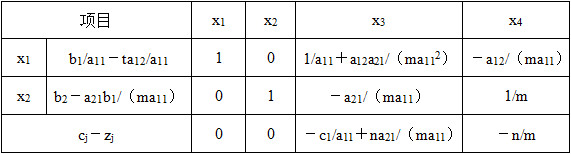
则根据已知一一对应,可得到以下方程
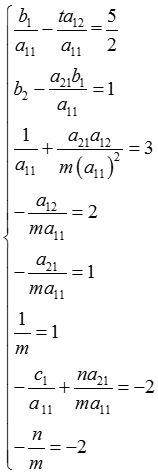
解得如下结果:
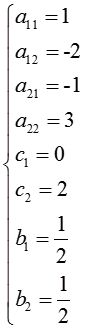
9 考虑线性规划问题
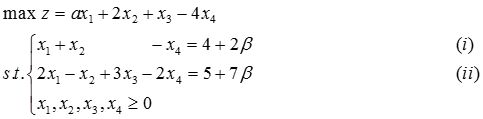
模型中α、β为参数,要求:
(1)组成两个新的约束(i)'=(i)+(ii),(ii)'=(ii)-2(i),根据式(i)'和式(ii)',以x l ,x 2 为基变量,列出初始单纯形表;
(2)在表中,假定β=0,则α为何值时,x 1 ,x 2 为问题的最优基;
(3)在表中,假定α=3,则β为何值时,x 1 ,x 2 为问题的最优基。
解: (1)由已知条件知,在新的约束条件下,新的线性规划模型如下:
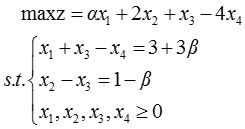
以x 1 ,x 2 为基变量,列出表(见表2-1-17):
表2-1-17
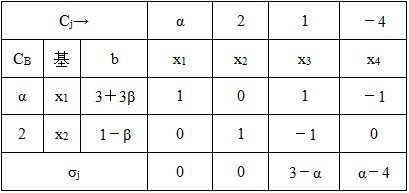
(2)如果β=0,则只需满足所有的检验数均非正即可,即
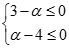 ,故当3≤α≤4时,x
1
,x
2
为问题的最优基变量;
,故当3≤α≤4时,x
1
,x
2
为问题的最优基变量;
(3)如果α=3,则只需满足所有b≥0成立即可,即
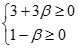 ,故当-1≤β≤1时,x
1
,x
2
为问题的最优基变量。
,故当-1≤β≤1时,x
1
,x
2
为问题的最优基变量。
10 试述线性规划模型中“线性”二字的含义,并用实例说明什么情况下线性的假设将被违背。
解: 线性的含义:一是严格的比例性,如生产某产品对资源的消耗量和可获取的利润,同其生产数量严格成比例;二是可叠加性,如生产多种产品时,可获取的总利润是各项产品的利润之和,对某项资源的消耗量应等于各产品对该资源的消耗量之和;三是可分性,即模型中的变量可以取值为小数、分数或某一实数;四是确定性,指模型中的参数c j ,a ij ,b i 均为确定的常数。
很多实际问题往往不符合上述条件,例如每件产品售价3元,但成批购买就可以得到折扣优惠。
11 判断下列说法是否正确,为什么?
(1)含n个变量m个约束的标准型的线性规划问题,基解数恰好为
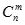 个;
个;
(2)线性规划问题的可行解如为最优解,则该可行解一定为基可行解;
(3)如线性规划问题存在可行域,则该可行域一定包含坐标的原点;
(4)单纯形法迭代计算中,必须选取同最大检验数σ j >0对应的变量作为换入基的变量。
解: (1)错误;
基本解的个数=基的个数≤C n m 。
(2)错误;
当有唯一最优解时,最优解是可行域顶点,对应基本可行解;当有无穷多最优解时,除了其中的可行域顶点对应基本可行解外,其余最优解不是基本可行解。
(3)错误;
如果约束条件中有一个约束所对应的区域不包含坐标的原点,则即使有可行域,也不包含坐标的原点。
(4)错误;
若此时最大检验数σ j >0,可是p j ≤0,则问题是无界解,计算结束。
12 线性规划问题max z=CX,AX=b,X≥0,如X * 是该问题的最优解,又λ>0为某一常数,分别讨论下列情况时最优解的变化。
(1)目标函数变为max z=λCX;
(2)目标函数变为max z=(C+λ)X;
(3)目标函数变为
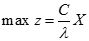 ,约束条件变为AX=λb。
,约束条件变为AX=λb。
解: (1)最优基不变;
由于X
*
是原问题的最优解,则满足
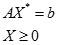 ,如果只是目标函数增大λ倍,而约束条件不发生变化的话,X
*
仍为新的线性规划的最优解,最优目标函数值为Z
*
=λX
*
。
,如果只是目标函数增大λ倍,而约束条件不发生变化的话,X
*
仍为新的线性规划的最优解,最优目标函数值为Z
*
=λX
*
。
(2)C为常数时最优解不变,否则可能发生变化;
由于X
*
是原问题的最优解,则满足
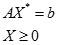 。
。
若C为常数向量,则目标函数值常数C倍,而约束条件不发生变化的话,X * 仍为新的线性规划的最优解,最优目标函数值为Z * =(λ+C)X * 。
若C不为常数向量,则新的线性规划的最优解一般会发生变化。
(3)最优解变为:λX * 。
由于X
*
是原问题的最优解,则满足
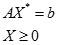 ,而约束条件发生变化,不妨设X′为新的线性规划问题的最优解,则满足
,而约束条件发生变化,不妨设X′为新的线性规划问题的最优解,则满足
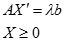 ,对其变形有
,对其变形有
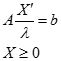 ,则
,则
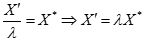 ,即新的最优解为X′=λX
*
,此时最优目标函数值
,即新的最优解为X′=λX
*
,此时最优目标函数值
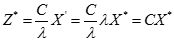 。故最优函数值保持不变,最优解为X′=λX
*
。
。故最优函数值保持不变,最优解为X′=λX
*
。
13 某饲养场饲养动物出售,设每头动物每天至少需700g蛋白质、30g矿物质、100mg维生素。现有五种饲料可供选用,各种饲料每kg营养成分含量及单价如表2-1-18所示。
表2-1-18
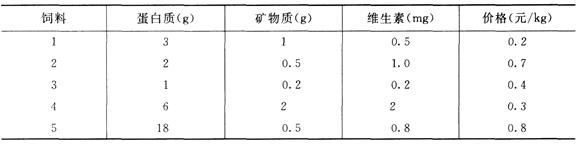
要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。
解: 设x i 表示第i种饲料数量,i=1,2,3,4,5
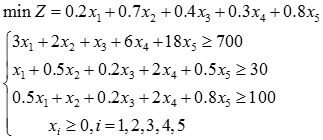
最优解为x 1 =x 2 =x 3 =0,x 4 =39.74,x 5 =25.64,z=32.44(元)
14 辽源街邮局从周一到周日每天所需的职员人数如表2-1-19所示。职员分别安排在周内某一天开始上班,并连续工作5天,休息2天。
表2-1-19

要求确定:
(1)该邮局至少应配备多少职员,才能满足值班需要;
(2)因从周一开始上班的,双休日都能休息;周二或周日开始上班的,双休日只能有一天得到休息;其他时间开始上班的,两个双休日都得不到休息,很不合理。因此邮局准备对每周上班的起始日进行轮换(但从起始日开始连续上5天班的规定不变),问如何安排轮换,才能做到在一个周期内每名职工享受到同等的双休日的休假天数;
(3)该邮局职员中有一名领班,一名副领班。为便于领导,规定领班于每周一、三、四、五、六上班,副领班于一、二、三、五、日这5天上班。据此试重新对上述要求(1)和(2)建模和求解。
解: (1)设x i (i=1,2,…,7)表示星期一至星期日开始上班的人数,则建立如下的数学模型。

解得最优解为X * =(6,3,3,7,0,3,1),z * =23
则该邮局至少应配备23名职员,才能满足值班需要。
(2)对这23名职工分别编号 ① , ② ,…,㉓,以23周为一个周期,这23名职工上下班安排见表2-1-20。
表2-1-20
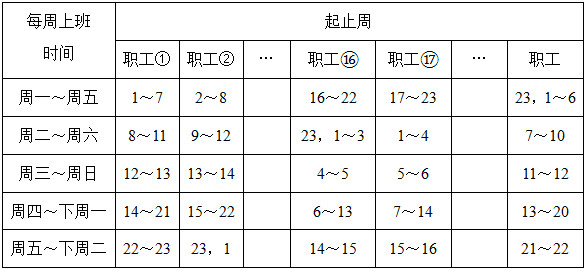
(3)此时只需在每天人数中减去领班和副领班两人即可,重新建模如下:
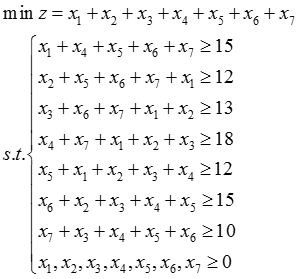
解得最优解为X * =(5,4,2,7,0,2,1),z * =21
则该邮局至少应配备21名职员,才能满足值班需要。
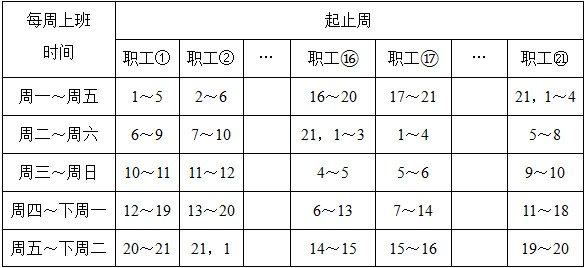
 对这21名职工分别编号
①
,
②
,…,㉑,以21周为一个周期,这21名职工上下班安排见表2-1-21。
对这21名职工分别编号
①
,
②
,…,㉑,以21周为一个周期,这21名职工上下班安排见表2-1-21。
表2-1-21
15 一艘货轮分前、中、后三个舱位,它们的容积与最大允许载重量如表2-1-22所示。现有三种货物待运,已知有关数据列于表2-1-23。
表2-1-22

表2-1-23

又为了航运安全,前、中、后舱的实际载重量大体保持各舱最大允许载重量的比例关系。具体要求:前、后舱分别与中舱之间载重量比例的偏差不超过15%,前、后舱之间不超过10%。问该货轮应装载A,B,C各多少件运费收入才最大?试建立这个问题的线性规划模型。
解: x ij 表示第i商品在舱j的装载量,i,j=1,2,3

16 长城通信公司拟对新推出的一款手机收费套餐服务进行调查,以便进一步设计改进。调查对象设定为商界人士及大学生,要求:
(1)总共调查600人,其中大学生不少于250人;
(2)方式分电话调查和问卷调查,其中问卷调查人数不少于30%;
(3)对大学生电话调查80%以上应安排在周六或周日,对商界人士电话调查80%以上应安排在周一至周五;
(4)问卷调查时间不限。已知有关调查费用如表2-1-24所示,问该公司应如何安排调查,使总的费用为最省。
表2-1-24
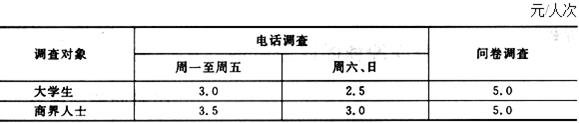
解: 设x 11 ,x 21 为周一至周五对大学生和商界人士电话调查人数,x 12 ,x 22 为双休日对上述人员电话调查人数,x 13 ,x 23 分别为问卷调查人数,则数学模型为
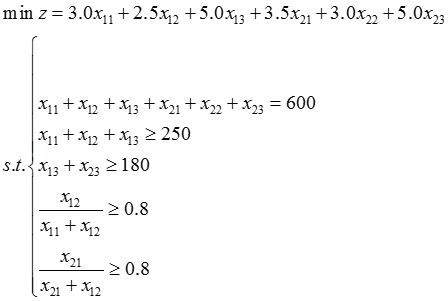
最优解x 11 =0,x 12 =420,x 13 =180,x 21 =0,x 22 =0,x 23 =0,z * =1950
17 生产存储问题。某厂签订了5种产品(i=1,…,5)上半年的交货合同。已知各产品在第j月(j=1,…,6)的合同交货量D ij ,该月售价s ij 、成本价c ij 及生产1件时所需工时a ij 。该厂第j月的正常生产工时为t i ,但必要时可加班生产,第j月允许的最多加班工时不超过t j ′,并且加班时间内生产出来的产品每件成本增加额外费用c ij ′元。若生产出来的产品当月不交货,每件库存1个月交存储费p i 元。试为该厂设计一个保证完成合同交货,又使上半年预期赢利总额为最大的生产计划安排。
解: 设x ij 为i种产品j月正常时间生产数,x ij ′为加班时间生产数,模型为

18 宏银公司承诺为某建设项目从2003年起的4年中每年初分别提供以下数额贷款:2003年——100万元,2004年——150万元,2005年——120万元,2006年——110万元。以上贷款资金均需于2002年年底前筹集齐。但为了充分发挥这笔资金的作用,在满足每年贷款额情况下,可将多余资金分别用于下列投资项目:
(1)于2003年年初购买A种债券,期限3年,到期后本息合计为投资额的140%,但限购60万元;
(2)于2003年年初购买B种债券,期限2年,到期后本息合计为投资额的125%,且限购90万元;
(3)于2004年年初购买C种债券,期限2年,到期后本息合计为投资额的130%,但限购50万元;
(4)于每年初将任意数额的资金存放于银行,年息4%,于每年底取出。
求宏银公司应如何运用好这笔筹集到的资金,使2002年年底需筹集到的资金数额为最少。
解: 设x ij (i为第1,2,3年初,j=1,2,3,4分别为A,B,C,D四类投资数)
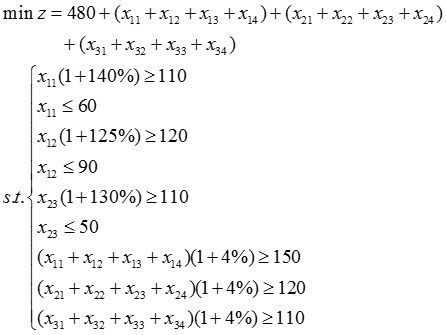
19 红豆服装厂新推出一款时装,据经验和市场调查,预测今后6个月内对该款时装的需求为:1月——3000件,2月——3600件,3月——4000件,4月——4600件,5月——4800件,6月——5000件。生产每件需熟练工人工作4h,耗用原材料150元,售价为240元/件。该厂1月初有熟练工80人,每人每月工作160h。为适应生产需要,该厂可招收新工人培训,但培训一名新工人需占用熟练工人50h用于指导操作,培训期为一个月,结束后即可上岗。熟练工人每月工资2000元,新工人培训期间给予生活补贴800元,转正后工资与生产效率同熟练工人。又熟练工人(含转正一个月后的新工人)每月初有2%因各种原因离职。已知该厂年初已加工出400件该款时装作为库存,要求6月末库存1000件。又每月生产出来时装如不在当月交货,库存费用为每件每月10元。试为该厂设计一个满足各月及6月末库存要求,又使1~6月总收入为最大的劳动力安排方案。
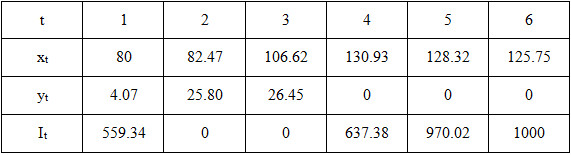
解: 设该厂每月初拥有熟练工人数x t (t=1,…,6),每月招收培训的新工人数为y t ,该厂月末库存为I t ,一月初库存为I 0 ,R t 为各月对时装的需求数,则数学模型为

解得z*=875122元,各月有关数字如表2-1-25所示。
表2-1-25
20 祥瑞贸易公司专门经营某种杂粮的批发业务。公司现有库容5000吨的仓库。1月1日公司拥有库存1000吨的杂粮,并有资金20000元。估计第一季度杂粮价格如表2-1-26所示。如买进的杂粮当月到货,则需到下月才能卖出,且规定“货到付款”。公司希望本季末库存为2000吨,问应采取什么样的买进与卖出的策略使3个月总的获利最大。要求列出本问题的线性规划模型,但不需求解。
表2-1-26
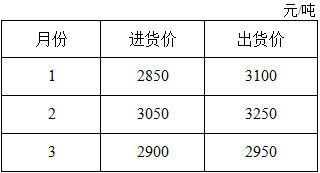
解: 设x i 表示第i月买入杂粮吨数,y i 表示第i月卖出杂粮吨数,i=1,2,3,则根据题意可列出: