





首先要明确什么是“信息”。广义上讲,信息就是消息。信息一般表现为5种形态:数据、文本、声音、图形、图像。本节主要讲述数据和文本的计算机表示和处理,声音、图形和图像的计算机表示和处理将在本书第6章中加以介绍。
在计算机中,一个带小数点的数据通常有两种表示方法:定点表示法和浮点表示法。在计算过程中小数点位置固定的数据称为定点数,小数点位置浮动的数据称为浮点数。
计算机中常用的定点数有两种,即定点纯整数和定点纯小数。将小数点固定在数的最低位之后,就是定点纯整数。将小数点固定在符号位之后、最高数值位之前,就是定点纯小数。
我们知道一个十进制数可以表示成一个纯小数与一个以10为底的整数次幂的乘积,如135.45可表示为0.135 45×10 3 。同理,一个任意二进制数 N 可以表示为下式:
N =2 J × S
其中, S 称为尾数,是二进制纯小数,表示 N 的有效数位; J 称为 N 的阶码,是二进制整数,指明了小数点的实际位置,改变 J 的值也就改变了数 N 的小数点的位置。该式也就是数的浮点表示形式,而其中的尾数和阶码分别是定点纯小数和定点纯整数。例如,二进制数111 01.11的浮点数表示形式可为:0.111 011 1×2 101 。

原码、反码和补码
2.数的编码表示
一般数都有正负之分,计算机只能记忆0和1,为了将数在计算机中存放和处理就要将数的符号进行编码。基本方法是在数中增加一位符号位(一般将其安排在数的最高位之前),并用“0”表示数的正号,用“1”表示数的负号,如:
数+1110011在计算机中可存为01110011;
数-1110011在计算机中可存为11110011。
这种数值位部分不变,仅用0和1表示其符号得到的数的编码,称为原码,并将原来的数称为真值,将其编码形式称为机器数。
按上述原码的定义和编码方法,数0就有两种编码形式:0000…0和100…0。对于带符号的整数来说, n 位二进制原码表示的数值范围是:-(2 n -1 -1)~+(2 n -1 -1)。
例如8位原码的表示范围为:-127~+127,16位原码的表示范围为:-32 767~+32 767。
为了简化运算操作,也为了把加法和减法统一起来以简化运算器的设计,计算机中也用到了其他的编码形式,主要有补码和反码。
为了说明补码的原理,先介绍数学中的“同余”概念。对于 a 、 b 两个数,若用一个正整数 K 去除,所得的余数相同,则称 a 、 b 对于模 K 是同余的(或称互补)。就是说, a 和 b 在模 K 的意义下相等,记作 a = b (MOD K )。
例如, a =13, b =25, K =12,用 K 去除 a 和 b 余数都是1,记作13=25(MOD 12)。
对钟表校对时间来说,顺时针方向拨 K (0≤ K ≤12)个小时与反时针方向拨(12- K )个小时其效果是相同的,就是因为在表盘上只有12个计数状态,即其模为12。
对于计算机,其运算器的位数(字长)总是有限的,即它也有“模”的存在,可以利用“补码”实现加减法之间的相互转换。下面仅给出求补码和反码的算法和应用举例。
(1)求反码的算法
对于正数,其反码和原码同形;对于负数,则将其原码的符号位保持不变,而将其他位按位求反(即将0换为1,将1换为0)。
(2)求补码的算法
对于正数,其补码和原码同形;对于负数,先求其反码,再在最低位加“1”(称为末位加1)。
求原码、反码和补码的计算,举例如表1.1所示(以8位代码为例)。
若对一补码再次求补就又得到了对应的原码。
表1.1 真值、原码、反码、补码对照举例

在二进制数的小数取舍中,0舍1入。例如,(0.82) 10 =(0.110100011…) 2 ,取8位小数,就把第9位上的1入到第8位,而第8位进位,从而得到十进制0.82的二进制数是0.11010010。在原码中,为了凑8位数字,把最后一个0舍去。-0.6的转换类似。
补码运算的基本规则是[ X ] 补 +[ Y ] 补 =[ X + Y ] 补 ,由此规律进行计算。
(1)18-13=5
由式18-13=18+(-13),则8位补码计算的竖式如下:
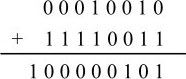
最高位进位自动丢失后,结果的符号位为0,即为正数,补码原码同形。转换为十进制数即为+5,运算结果正确。
(2)25-36=-11
由式25-36=25+(- 36),则8位补码计算的竖式如下:
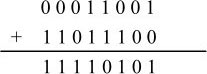
结果的符号位为1,即为负数。由于负数的补码原码不同形,所以要将其求补得到原码:1 0 0 0 1 0 1 1,再转换为十进制数即为-11,运算结果正确。
前面已经了解了数的浮点表示形式,即阶码和尾数的表示形式。原则上讲,阶码和尾数都可以任意选用原码、补码或反码,这里仅简单举例说明采用补码表示的定点纯整数表示阶码、采用补码表示的定点纯小数表示尾数的浮点数表示方法。例如,在IBM PC系列微机中,采用4个字节存放一个实型数据,其中阶码占1个字节,尾数占3个字节。阶码的符号(简称阶符)和数值的符号(简称数符)各占一位,且阶码和尾数均为补码形式。当存放十进制数+256.8125时,其浮点格式为:
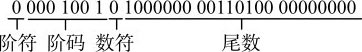
即(256.8125) 10 =(0.1000000001101×2 1001 ) 2 。
当存放十进制数-0.21875时,其浮点格式为:
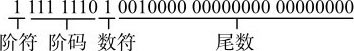
即(-0.21875) 10 =(-0.00111) 2 =(-0.111×2 -010 ) 2 。
由上例可以看到,当写一个编码时必须按规定写足位数。另外,为了充分利用编码表示高的数据精度,计算机中采用了“规格化”的浮点数的概念,即尾数小数点的后一位必须是非“0”。即对正数小数点的后一位必须是“1”;对负数补码,小数点的后一位必须是“0”。
由于计算机只能识别二进制代码,数字、字母、符号等必须以特定的二进制代码来表示,称为它们的二进制编码。
前面的学习中提到当十进制小数转换为二进制数时将会产生误差,为了精确地存储和运算十进制数,可用若干位二进制数来表示一位十进制数,称为二进制编码的十进制数,简称二—十进制代码(Binary Code Decimal,BCD)。由于十进制数有10个数码,起码要用4位二进制数才能表示1位十进制数,而4位二进制数能表示16个符号,所以就存在有多种编码方法。其中 8421码是常用的一种,它利用了二进制数的展开表达式形式,即各位的位权由高位到低位分别是8、4、2、1,方便了编码和解码的运算操作。若用BCD码表示十进制数2365就可以直接写出结果:0010 0011 0110 0101。
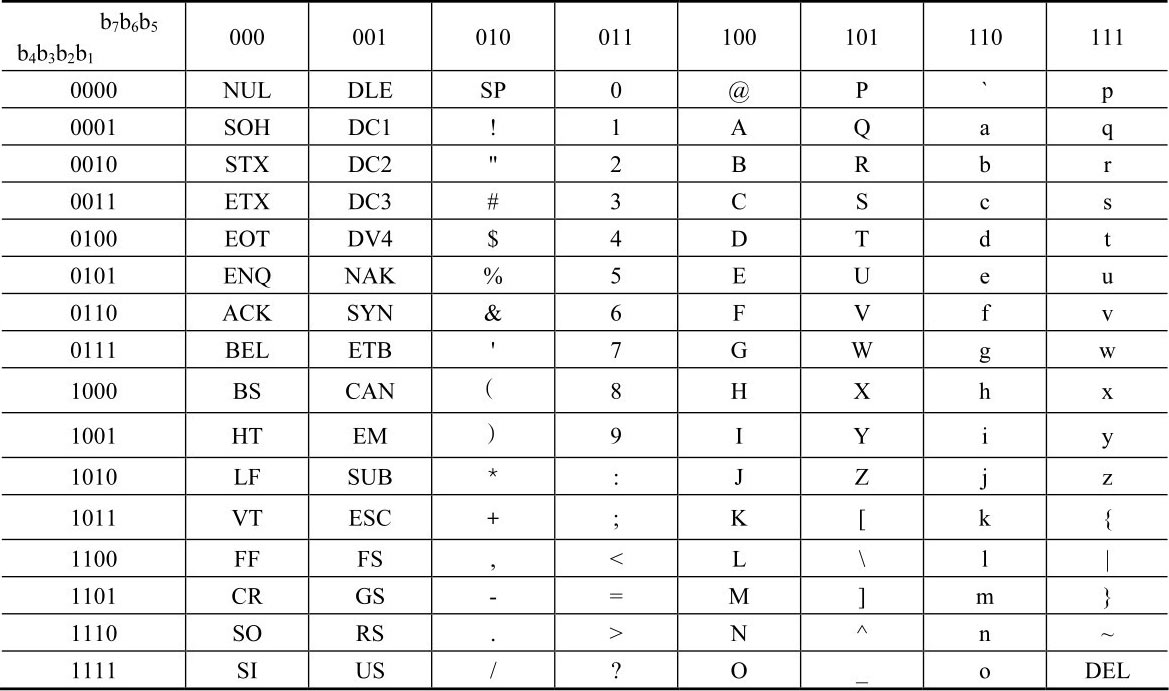
在英语书中用到的字母为52个(大、小写字母各26个),数码10个,数学运算符号和其他标点符号等约32个,再加上用于控制打印机等外围设备的控制字符,共计128个符号。对128个符号编码需要7位二进制数,且可以有不同的排列方式,即不同的编码方案。其中ASCII代码(American Standard Code for Information Interchange,美国标准信息交换码)是使用最广泛的字符编码方案。在7位ASCII 代码之前再增加一位用作校验位,形成8位编码。ASCII编码表如表1.2所示。
表1.2 ASCII编码表(b 7 b 6 b 5 b 4 b 3 b 2 b 1 )
依据汉字处理阶段的不同,汉字编码可分为输入码、显示字形码、机内码和交换码。
① 在键盘输入汉字用到的汉字输入码归纳起来可分为数字码、拼音码、字形码和音形混合码。数字码以区位码、电报码为代表,一般用4位十进制数表示一个汉字,每个汉字编码唯一,记忆困难。拼音码又分全拼和双拼,基本上无需记忆,但重音字太多。为此又提出双拼双音、智能拼音和联想等方案,推进了拼音汉字编码的普及使用。字形码以五笔字形为代表,优点是重码率低,适用于专业打字人员应用,缺点是记忆量大。自然码则将汉字的音、形、义都反映在其编码中,是混合编码的代表。
② 要在屏幕或在打印机上输出汉字,就需要用到汉字的字形信息。目前表示汉字字形常用点阵字形法和矢量法。
点阵字形是将汉字写在一个方格纸上,用一位二进制数表示一个方格的状态,有笔画经过记为“1”,否则记为“0”,并称其为点阵。把点阵上的状态代码记录下来就得到一个汉字的字形码。将字形信息有组织地存放起来就形成汉字字形库。一般的汉字系统中汉字字形点阵有16×16、24×24、48×48几种,点阵越大对每个汉字的修饰作用就越强,打印质量也就越高,通常用16×16点阵来显示汉字。
矢量字形则是通过抽取并存放汉字中每个笔画的特征坐标值,即汉字的字形矢量信息,在输出时依据这些信息经过运算恢复原来的字形。所以矢量字形信息可适应显示和打印各种字号的汉字。
③ 当输入一个汉字并要将其显示出来,就要将其输入码转换成为能表示其字形码存储地址的机内码。根据字库的选择和字库存放位置的不同,同一汉字在同一计算机内的内码也将是不同的。
④ 汉字的输入码、字形码和机内码都不是唯一的,不便于不同计算机系统之间的汉字信息交换。为此我国制定了《信息交换用汉字编码字符集基本集》(GB 2312—1980),提供了统一的国家信息交换用汉字编码,称为国标码。该标准集中规定了682个西文字符和图形符号、6 763个常用汉字。
除GB 2312—1980外,GB 7589—1987和GB 7590—1987两个辅助集也对非常用汉字做出了规定,三者共定义汉字21 039个。

计算机的由来与发展

杰出人物简介