下载掌阅APP，畅读海量书库
立即打开
1 函数f（x）＝（x－x 3 ）/sinπx的可去间断点的个数为（ ）。
A．1
B．2
C．3
D．无穷多个
【答案】 C
【考点】 间断点的类型
【解析】 首先找出使f（x）无定义的点：即满足sinπx＝0的点，得x＝0，±1，±2，±3，…，若上述点为可去间断点，则f（x）在该点的左右极限存在且相等，又sinπx＝0，则必有分子x－x 3 ＝0，即可去间断点可能为x＝0，±1。又
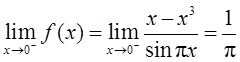
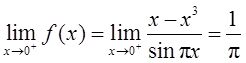
所以
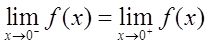
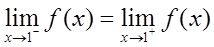
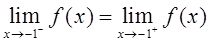
综上可知，可去间断点有3个。
2 当x→∞时，f（x）＝x－sinax与g（x）＝x 2 ln（1－bx）为等价无穷小，则（ ）。
A．a＝1，b＝－1/6
B．a＝1，b＝1/6
C．a＝－1，b＝－1/6
D．a＝－1，b＝1/6
【答案】 A
【考点】 等价无穷小的定义
【解析】 当x→0时，有
f（x）＝x－sinax＝x－[ax－（ax） 3 /3！＋ο（x 3 ）]＝（1－a）x＋（ax） 3 /3！－ο（x 3 ）
g（x）＝x 2 ln（1－bx）～（－bx 3 ）
由于f（x）＝x－sinax与g（x）＝x 2 ln（1－bx）为等价无穷小，则
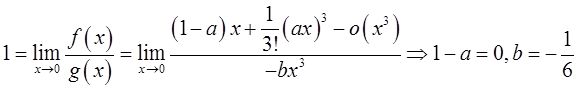
故a＝1，b＝－1/6。
3 使不等式
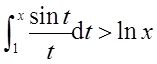
成立的x的范围是（ ）。
A．（0，1）
B．（1，π/2）
C．（π/2，π）
D．（π，＋∞）
【答案】 A
【考点】 积分的计算和比较大小
【解析】
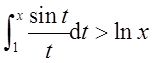
等价于
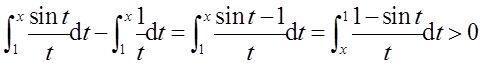
又在上述四个区间内，（1－sint）/t＞0，故若要使上式成立，则须0＜x＜1。
4 设函数y＝f（x）在区间[－1，3]上的图形如图1所示。
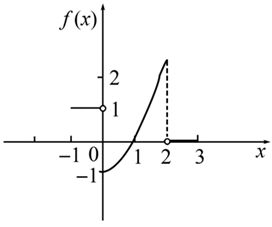
图1
则
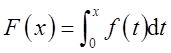的图形为（ ）。
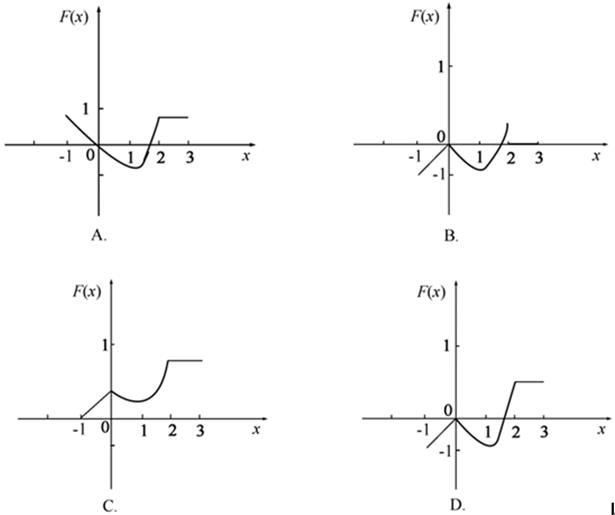
【答案】 D
【考点】 定积分的应用
【解析】 由图可知：
（Ⅰ）在区间（－1，0）上，f（x）≥0，则F（x）在此区间单调递增，排除A项。
（Ⅱ）
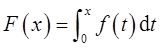
表示y＝f（x），x＝0，x＝x 0 与x轴所围曲边梯形位于x轴上方的图形面积减去位于x轴下方的图形面积所得差值，则当0＜x＜1时，由图可知
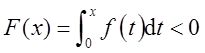
排除C项。
（Ⅲ）又当2＜x＜3时，f（x）＝0，故
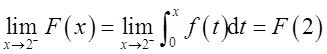
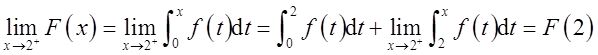
即F（x）在x＝2处连续，排除B项。
5
设A，B均为2阶矩阵，A
*
，B
*
分别为A，B的伴随矩阵，若|A|＝2，|B|＝3，则分块矩阵
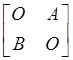的伴随矩阵为（ ）。
A．
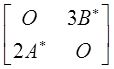
B．
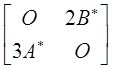
C．
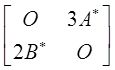
D．
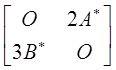
【答案】 B
【考点】 伴随矩阵
【解析】 由于
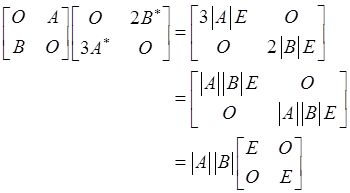
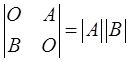
因此选项B正确。
6 设A，P均为3阶矩阵，P T 为P的转置矩阵，且
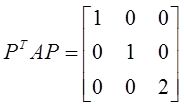
若P＝（α 1 ，α 2 ，α 3 ），Q＝（α 1 ＋α 2 ，α 2 ，α 3 ），则Q T AQ为（ ）。
A．
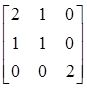
B．
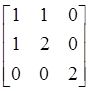
C．
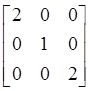
D．
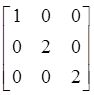
【答案】 A
【考点】 矩阵的计算
【解析】 由题设可知
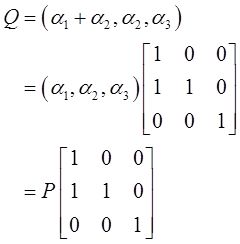
于是
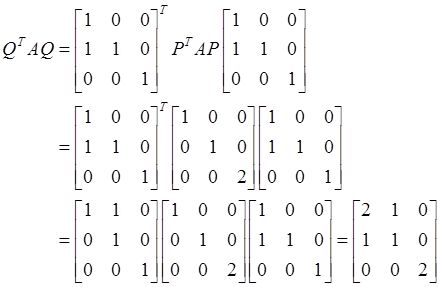
7 设事件A与事件B互不相容，则（ ）。
A．P（ A B ）＝0
B．P（AB）＝P（A）P（B）
C．P（A）＝1－P（B）
D．P（ A ∪ B ）＝1
【答案】 D
【考点】 概率的基本公式
【解析】 由题意可知，
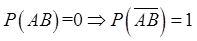
即P（ A ∪ B ）＝1。
8 设随机变量X与Y相互独立，且X服从标准正态分布N（0，1），Y的概率分布为P{Y＝0}＝P{Y＝1}＝1/2，记F Z （z）为随机变量Z＝XY的分布函数，则函数F Z （z）的间断点的个数为（ ）。
A．0
B．1
C．2
D．3
【答案】 B
【考点】 概率分布和函数的间断点
【解析】 F Z （z）＝P{Z≤z}＝P{XY≤z}＝P{XY≤z|Y＝0}P{Y＝0}＋P{XY≤z|Y＝1}P{Y＝1}＝P{0≤z}/2＋P{X≤z}/2。
当z≤0时，F Z （z）＝P{X≤z}/2＝Φ X （z）/2；当z＞0时，F Z （z）＝1/2＋P{X≤z}/2＝1/2＋Φ X （z）/2。于是
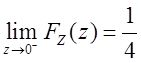
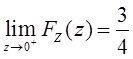
故z＝0为F Z （z）的间断点。
9
______。
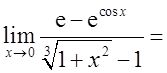【答案】 3e/2
【考点】 极限的计算
【解析】
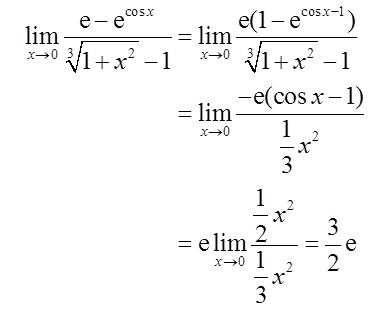
10
设z＝（x＋e
y
）
x
，则
______。
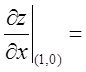【答案】 2ln2＋1
【考点】 多元函数的偏微分
【解析】
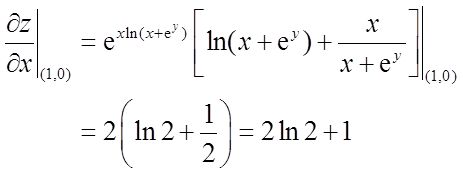
11
幂级数
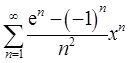的收敛半径为______。
【答案】 e － 1
【考点】 幂级数的收敛半径
【解析】
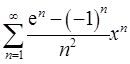的收敛半径为
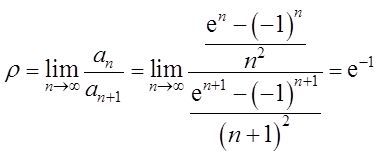
12 设某产品的需求函数为Q＝Q（p），其对价格p的弹性ε p ＝0.2，则当需求量为10000件时，价格增加一元会使产品收益增加______元。
【答案】 8000
【考点】 导数的经济意义——边际、弹性的概念及计算
【解析】 由题意知，收益函数为L＝Qp，于是L′＝Q′p＋Q。又ε p ＝－Q′p/Q＝0.2，则Q′p＝－0.2Q，即L′＝0.8Q，L′| Q ＝ 10000 ＝0.8Q| Q ＝ 10000 ＝8000，即价格增加一元会使产品收益增加8000元。
13
设α＝（1，1，1）
T
，β＝（1，0，k）
T
。若矩阵αβ
T
相似于
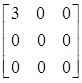，则k＝______。
【答案】 2
【考点】 矩阵的相似
【解析】
β
T
α为一实数，其值等于矩阵αβ
T
的主对角线元素之和。又矩阵αβ
T
相似于
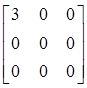，则
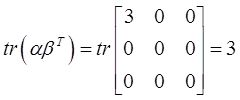
故3＝β T α＝1＋k，即k＝2。
14 设X 1 ，X 2 ，…，X m 为来自二项分布总体B（n，p）的简单随机样本， X 和S 2 分别为样本均值和样本方差。设T＝ X －S 2 ，则ET＝______。
【答案】 np 2
【考点】 二项分布和期望的计算
【解析】 由题意可得E X ＝np，ES 2 ＝np（1－p），ET＝E（ X －S 2 ）＝E X －ES 2 ＝np－np（1－p）＝np 2 。
三、解答题（15～23小题，共94分，解答应写出文字说明、证明过程或演算步骤。）
15 （本题满分9分）
求二元函数f（x，y）＝x 2 （2＋y 2 ）＋ylny的极值。
【考点】 二元函数的极值
解： 由题意，令
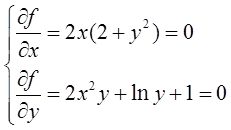
解得唯一驻点（0，1/e）。
由于
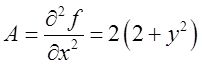
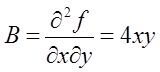
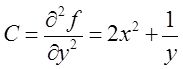
于是（B 2 －AC）| （ 0 ， 1/e ） ＝[16x 2 y 2 －2（2＋y 2 ）（2x 2 ＋1/y）]| （ 0 ， 1/e ） ＝－2e（2＋1/e 2 ）＜0，且A＞0。故（0，1/e）为函数f（x，y）的极小值点，且极小值为f（0，1/e）＝－1/e。
16 （本题满分10分）
计算不定积分
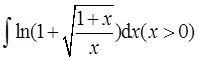
【考点】 不定积分的计算（换元积分）
解： 令
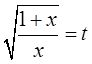
则x＝1/（t 2 －1），于是
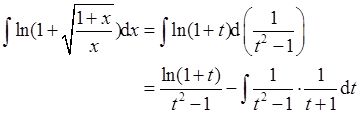
而
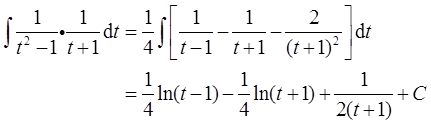
C为任意常数。故
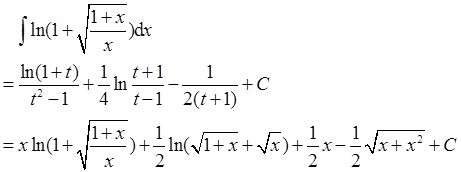
17 （本题满分10分）
计算二重积分
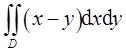，其中D＝{（x，y）|（x－1）
2
＋（y－1）
2
≤2，y≥x}。
【考点】 二重积分的计算
解： 方法一：如图2所示。
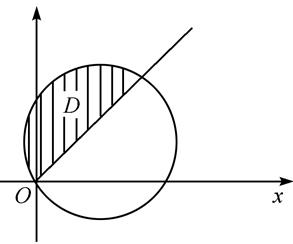
图2
区域D的极坐标表示为：0≤ρ≤2（sinθ＋cosθ），π/4≤θ≤3π/4。
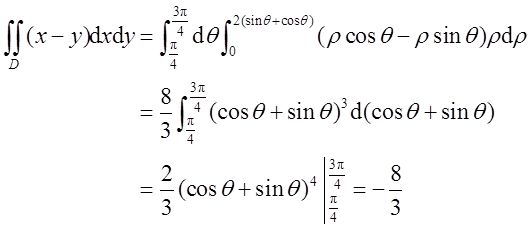
方法二：将区域D分成D 1 ，D 2 两部分（如图3所示）：
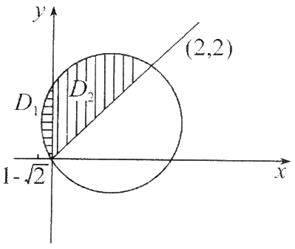
图3
其中
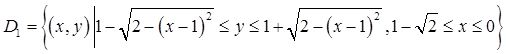
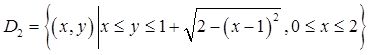
由二重积分的性质知，
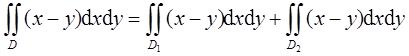
又
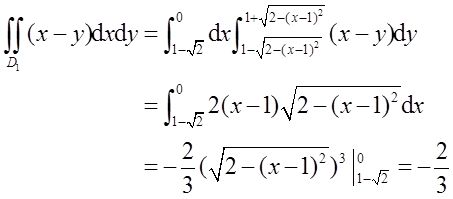
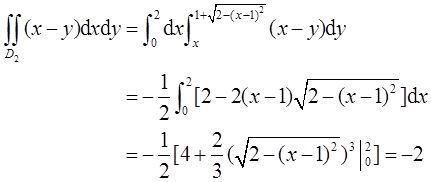
故
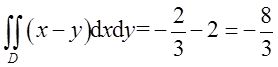
18 （本题满分11分）
（Ⅰ）证明拉格朗日中值定理：若函数f（x）在[a，b]上连续，在（a，b）内可导，则存在ξ∈（a，b），使得f（b）－f（a）＝f′（ξ）（b－a）；
（Ⅱ）证明：若函数f（x）在x＝0处连续，在（0，δ）（δ＞0）内可导，且
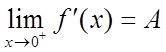
则f ＋ ′（0）存在，且f ＋ ′（0）＝A。
【考点】 拉格朗日中值定理和罗尔中值定理
证： （Ⅰ）取F（x）＝f（x）－{[f（b）－f（a）]（x－a）}/（b－a），由题意知，F（x）在[a，b]上连续，在（a，b）内可导，且F（a）＝f（a）－{[f（b）－f（a）]（a－a）}/（b－a）＝f（a），F（b）＝f（b）－{[f（b）－f（a）]（b－a）}/（b－a）＝f（a）。根据罗尔定理得，存在ξ∈（a，b），使得F′（ξ）＝f′（ξ）－[f（b）－f（a）]/（b－a）＝0，即f（b）－f（a）＝f′（ξ）（b－a）。
（Ⅱ）对于任意的t∈（0，δ），有f（x）在[0，t]上连续，（0，t）内可导，由右导数定义及拉格朗日中值定理有，
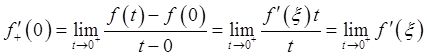
其中ξ∈（0，t）。
由于
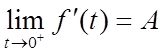
且当t→0 ＋ 时，ξ→0 ＋ ，所以
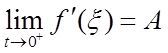
故f ＋ ′（0）存在，且f ＋ ′（0）＝A。
19 （本题满分10分）
设曲线y＝f（x），其中f（x）是可导函数，且f（x）＞0。已知曲线y＝f（x）与直线y＝0，x＝1及x＝t（t＞1）所围成的曲边梯形绕x轴旋转一周所得的立体体积值是该曲边梯形面积值的πt倍，求该曲线的方程。
【考点】 旋转体的体积
解： 由题意知，
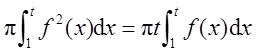
在等式两边对t求导得，
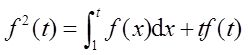
将t＝1代入上式得f（1）＝1或f（1）＝0（舍去）。再求导得：2f（t）f′（t）＝2f（t）＋tf′（t），记f（t）＝y，则dt/dy＋t/2y＝1，故
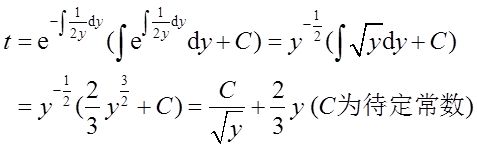
将t＝1，y＝1代入得C＝1/3，从而
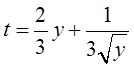
故所求曲线方程为
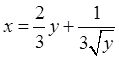
20 （本题满分11分）
设
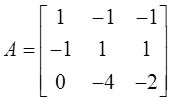
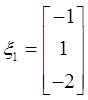
（Ⅰ）求满足Aξ 2 ＝ξ 1 ，A 2 ξ 3 ＝ξ 1 的所有向量ξ 2 ，ξ 3 ；
（Ⅱ）对（Ⅰ）中的任意向量ξ 2 ，ξ 3 证明ξ 1 ，ξ 2 ，ξ 3 线性无关。
【考点】 矩阵的秩和向量组的相关性
解： （Ⅰ）
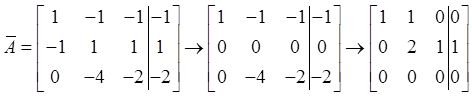
于是r（A）＝r（ A ）＝2，取x 2 为自由变量，可得x 3 ＝－2x 2 ＋1，x 1 ＝－x 2 。故
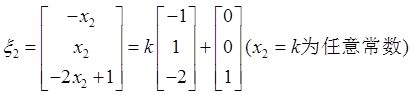
设
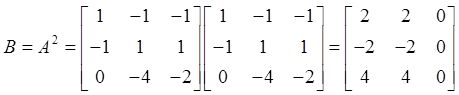
则
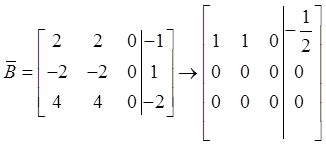
于是r（B）＝r（ B ）＝1，取x 2 ，x 3 为自由变量，则x 1 ＝－x 2 －1/2，故
（Ⅱ）证法1：由（Ⅰ）知
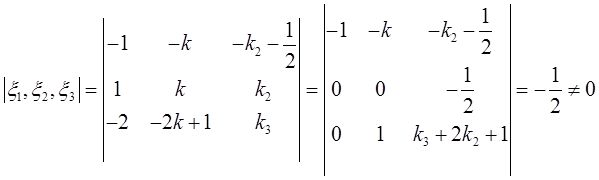
故ξ 1 ，ξ 2 ，ξ 3 线性无关。
证法2：由题设可得Aξ 1 ＝0。设存在一组数k 1 ，k 2 ，k 3 使得k 1 ξ 1 ＋k 2 ξ 2 ＋k 3 ξ 3 ＝0①，在等式两端左乘A，得k 1 Aξ 1 ＋k 2 Aξ 2 ＋k 3 Aξ 3 ＝0，即k 2 Aξ 2 ＋k 3 Aξ 3 ＝0，即k 2 ξ 1 ＋k 3 Aξ 3 ＝0②，再在等式两端左乘A，得k 2 Aξ 1 ＋k 3 A 2 ξ 3 ＝0，即k 3 ξ 1 ＝0，于是k 3 ＝0，代入②式得k 2 ξ 1 ＝0，故k 2 ＝0。将k 2 ＝k 3 ＝0代入①式可得k 1 ＝0，从而ξ 1 ，ξ 2 ，ξ 3 线性无关。
21 （本题满分11分）
设二次型f（x 1 ，x 2 ，x 3 ）＝ax 1 2 ＋ax 2 2 ＋（a－1）x 3 2 ＋2x 1 x 3 －2x 2 x 3 。
（Ⅰ）求二次型f的矩阵的所有特征值；
（Ⅱ）若二次型f的规范型为y 1 2 ＋y 2 2 ，求a的值。
【考点】 矩阵的特征值和二次型的规范型
解： （Ⅰ）由题设知，二次型f的矩阵为
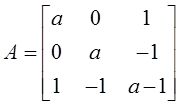
由于
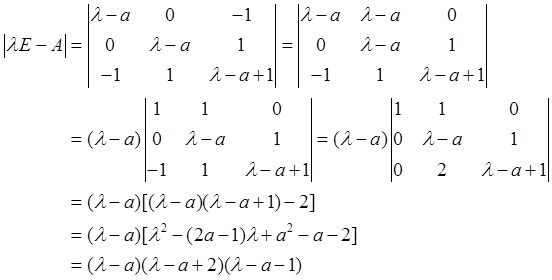
于是f的矩阵A所有的特征值为λ 1 ＝a，λ 2 ＝a－2，λ 3 ＝a＋1。
（Ⅱ）若二次型f的规范型为y 1 2 ＋y 2 2 ，则它的正惯性指数为2。于是f的矩阵A的特征值中有两个大于零，一个为零．显然λ 3 ＞λ 1 ＞λ 2 ，故λ 2 ＝a－2＝0，即a＝2。
22 （本题满分11分）
设二维随机变量（X，Y）的概率密度为
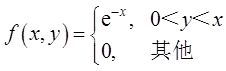
（Ⅰ）求条件概率密度f Y|X （y|x）；
（Ⅱ）求条件概率P{X≤1|Y≤1}。
【考点】 二维随机变量条件概率密度
解： （Ⅰ）X的概率密度为
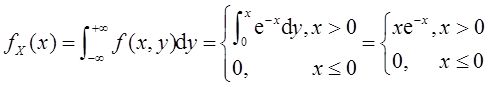
当x＞0时，有
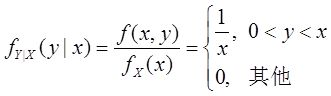
（Ⅱ）y的概率密度为
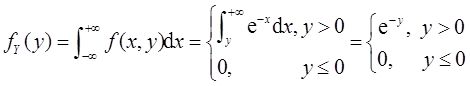
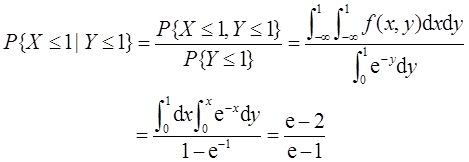
23 （本题满分11分）
袋中有1个红球、2个黑球与3个白球，现有放回地从袋中取两次，每次取一个球。以X，Y，Z分别表示两次取球所取得的红球、黑球与白球的个数。
（Ⅰ）求P{X＝1|Z＝0}；
（Ⅱ）求二维随机变量（X，Y）的概率分布。
【考点】 二维离散型随机变量概率和概率分布的计算
解： 由于本题是有放回地取球，则基本事件总数为36。
（Ⅰ）P{X＝1|Z＝0}＝P{X＝1，Z＝0}/P{Z＝0}＝[（1×2＋2×1）/36]/[（3×3）/36]＝4/9。
（Ⅱ）X，Y的可能取值均为0，1，2，且
P{X＝0，Y＝0}＝（3×3）/36＝1/4
P{X＝0，Y＝1}＝（2×2×3）/36＝1/3
P{X＝0，Y＝2}＝（2×2）/36＝1/9
P{X＝1，Y＝0}＝（2×1×3）/36＝1/6
P{X＝1，Y＝1}＝（2×1×2）/36＝1/9
P{X＝1，Y＝2}＝0
P{X＝2，Y＝0}＝（1×1）/36＝1/36
P{X＝2，Y＝1}＝0
P{X＝2，Y＝2}＝0
故二维随机变量f（x，y）的概率分布如表1所示。
表1
