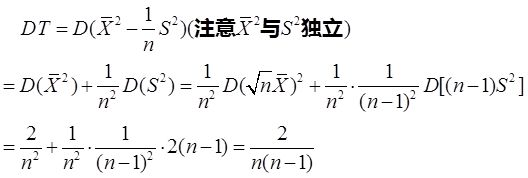下载掌阅APP，畅读海量书库
立即打开
1
设函数f（x）在区间[－1，1]上连续，则x＝0是函数
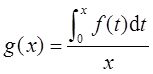的（ ）。
A．跳跃间断点
B．可去间断点
C．无穷间断点
D．振荡间断点
【答案】 B
【考点】 函数间断点的类型
【解析】
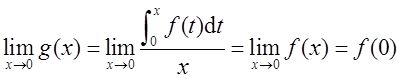
首先利用间断点的定义确定该点为间断点，然后利用如下的间断点的类型进行判断。
第一类间断点：x＝x
0
为函数f（x）的间断点，且
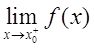与
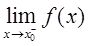均存在，则称x＝x
0
为函数f（x）的第一类间断点，其中：
①跳跃型间断点：
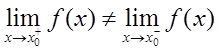
②可去型间断点：
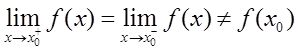
第二类间断点：x＝x
0
为函数f（x）的间断点，且
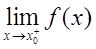与
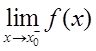之中至少有一个不存在，则称x＝x
0
为函数f（x）的第二类间断点，其中：
①无穷型间断点：
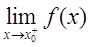与
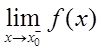至少有一个为∞；
②振荡型间断点：
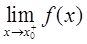或
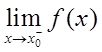为振荡型，极限不存在。
由于题设中g（0）不存在，故x＝0是函数g（x）的可去间断点。
2
如图1，曲线段的方程为y＝f（x），函数f（x）在区间[0，a]上有连续的导数，则定积分
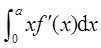等于（ ）。
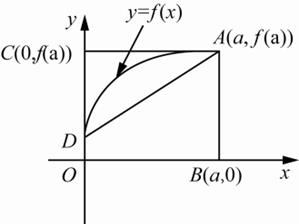
图1
A．曲边梯形ABOD的面积
B．梯形ABOD的面积
C．曲边三角形ACD的面积
D．三角形ACD的面积
【答案】 C
【考点】 积分的几何意义
【解析】
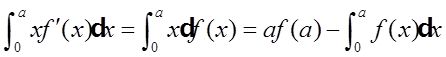
而
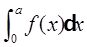表示曲边梯形OBAD的面积，故
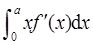表示曲边三角形ACD的面积。
3 已知
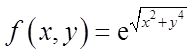
则函数在原点偏导数存在的情况是（ ）。
A．f x ′（0，0），f y ′（0，0）都存在
B．f x ′（0，0）不存在，f y ′（0，0）存在
C．f x ′（0，0）存在，f y ′（0，0）不存在
D．f x ′（0，0），f y ′（0，0）都不存在
【答案】 B
【考点】 二元函数的偏导数的定义
【解析】 由偏导数的定义知
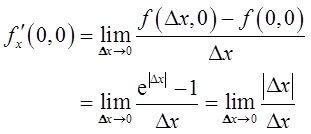
不存在；
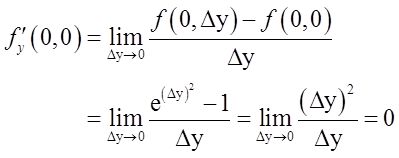
存在。
4 设函数f（x）连续，
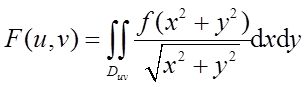
其中区域D uv 为图2中阴影部分，则∂F/∂u＝（ ）。
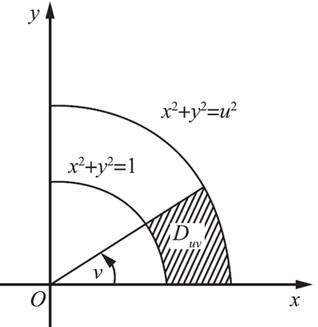
图2
A．vf（u 2 ）
B．vf（u 2 ）/u
C．vf（u）
D．vf（u）/u
【答案】 A
【考点】 利用极坐标变换计算二重积分
【解析】 利用极坐标，得
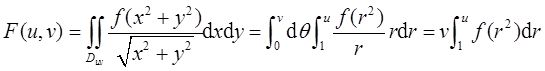
所以∂F/∂u＝vf（u 2 ）。
5 设A为n阶非零矩阵，E为n阶单位矩阵，若A 3 ＝O，则（ ）。
A．E－A不可逆，E＋A不可逆
B．E－A不可逆，E＋A可逆
C．E－A可逆，E＋A可逆
D．E－A可逆，E＋A不可逆
【答案】 C
【考点】 矩阵可逆的判定
【解析】 A 3 ＝O⇒A 3 ＋E＝E⇒（A＋E）（A 2 －A＋E）＝E，则A＋E可逆，A 3 ＝O⇒A 3 －E＝－E⇒（E－A）（A 2 ＋A＋E）＝E，即E－A可逆。
6
设
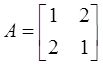，则实数域上与A合同的矩阵是（ ）。
A．
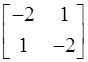
B．
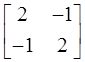
C．
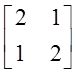
D．
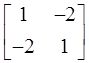
【答案】 D
【考点】 矩阵合同的判定
【解析】
由题意易知
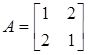为实对称矩阵，进而得A的特征值为－1，3，则x
T
Ax的正负惯性指数分别为1，1。可以求出选项中各矩阵的特征值，
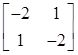的特征值为－1，－3；
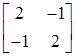的特征值为1，3；
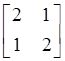的特征值为1，3；
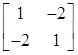的特征值为－1，3，知只有D项中矩阵符合。
7 设随机变量X，Y独立同分布，且X的分布函数为F（x），则Z＝max{X，Y}的分布函数为（ ）。
A．F 2 （x）
B．F（x）F（y）
C．1－[1－F（x）] 2
D．[1－F（x）][1－F（y）]
【答案】 A
【考点】 求分布函数
【解析】 由X，Y独立同分布知，Y的分布函数也为F（x）。记Z的分布函数为F Z （x），则
F Z （x）＝P{max{X，Y}≤x}＝P{X≤x，Y≤x}＝P{X≤x}P{Y≤x}（X与Y独立）＝F 2 （x）
8 随机变量X～N（0，1），Y～N（1，4），相关系数ρ XY ＝1，则（ ）。
A．P{Y＝－2X－1}＝1
B．P{Y＝2X－1}＝1
C．P{Y＝－2X＋1}＝1
D．P{Y＝2X＋1}＝1
【答案】 D
【考点】 相关系数及其性质
【解析】 方法一：由X～N（0，1），Y～N（1，4）知EX＝0，DX＝1，EY＝1，DY＝4。由于ρ XY ＝1，所以存在常数a，b，使得P{Y＝aX＋b}＝1，从而EY＝aEX＋b，得b＝1，而
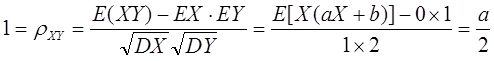
得a＝2，故应选D项。
方法二：本题利用排除法。由ρ XY ＝1，可知X，Y正相关，排除A、C、B项。若Y＝2X－1，由EX＝0，得到EY＝－1，排除B，可知应选D。
9 设函数
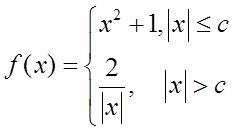
在（－∞，＋∞）上连续，则c＝______。
【答案】 1
【考点】 函数连续性的判定
【解析】 由题意知，
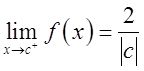
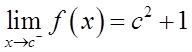
f（c）＝c 2 ＋1，若
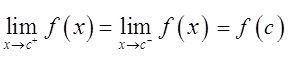
则c＝1。
10
设函数f[x＋（1/x）]＝（x＋x
3
）/（1＋x
4
），则
______。
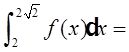【答案】 （ln3）/2
【考点】 积分的计算方法
【解析】 由
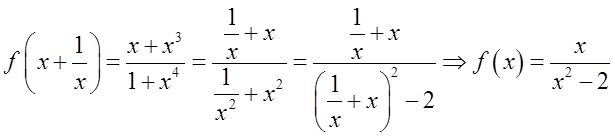
得
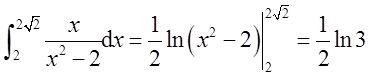
11
设D＝{（x，y）|x
2
＋y
2
≤1}，则
______。
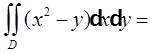【答案】 π/4
【考点】 二重积分的计算
【解析】 由于积分区域D关于x轴，y轴对称，所以有
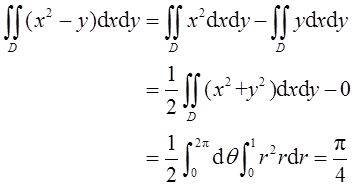
12 微分方程为xy′＋y＝0满足条件y（1）＝1的解y＝______。
【答案】 1/x
【考点】 微分方程的求解
【解析】 由题意得，xy′＋y＝0⇒y′/y＝－1/x，两边积分得y＝C/x，C为待定常数，将y（1）＝1代入得C＝1，即y＝1/x。
13 设三阶矩阵A的特征值是1，2，2，E为三阶单位矩阵，则|4A － 1 －E|＝______。
【答案】 3
【考点】 矩阵的特征值与行列式之间的关系
【解析】 由于A － 1 的特征值是1，1/2，1/2，从而4A － 1 －E的特征值是3，1，1，即|4A － 1 －E|＝3×1×1＝3。
14 设随机变量X服从参数为1的泊松分布，则P{X＝EX 2 }＝______。
【答案】 1/（2e）
【考点】 泊松分布及其概率分布
【解析】 服从参数为1的泊松分布的概率分布为：P{X＝i}＝e －1 /i！。又EX 2 ＝DX＋（EX） 2 ＝1＋1＝2，故P{X＝EX 2 }＝P{X＝2}＝（e － 1 ）/2＝1/（2e）。
三、解答题（15～23小题，共94分，解答应写出文字说明、证明过程或演算步骤。）
15 （本题满分9分）
计算
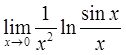
【考点】 极限的求解方法（洛必达法则）
解： 利用下列等价无穷小
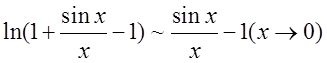
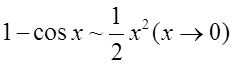
由
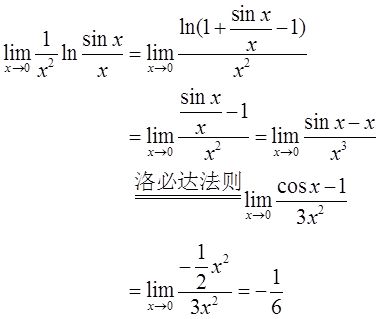
16 （本题满分10分）
设x＝z（x，y）是由方程x 2 ＋y 2 －z＝φ（x＋y＋z）所确定的函数，其中φ具有二阶导数，且φ′≠1。
（Ⅰ）求dz；
（Ⅱ）记u（x，y）＝（∂z/∂x－∂z/∂y）/（x－y），求∂u/∂x。
【考点】 多元函数的微分计算
解： （Ⅰ）在方程x 2 ＋y 2 －z＝φ（x＋y＋z）两端求微分得2xdx＋2ydy－dz＝φ′（x＋y＋z）（dx＋dy＋dz），即dz＝[（2x－φ′）dx＋（2y－φ′）dy]/（φ′＋1）。
（Ⅱ）
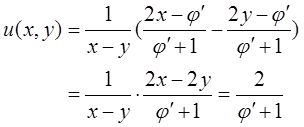
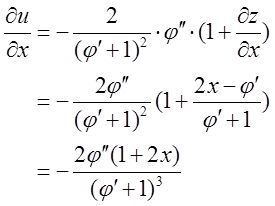
17 （本题满分11分）
计算
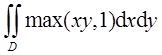，其中D＝{（x，y）|0≤x≤2，0≤y≤2}。
【考点】 二重积分的计算
解： 曲线xy＝1将区域D分成如图3所示的两个区域D 1 和D 2 。则有
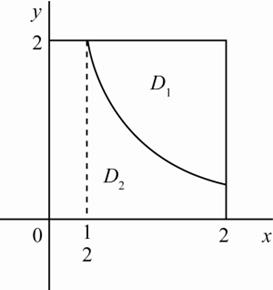
图3
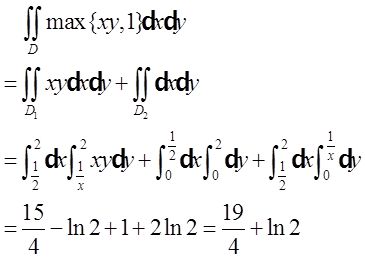
18 （本题满分10分）
设f（x）是周期为2的连续函数。
（Ⅰ）证明：对任意的实数t，有
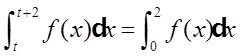
（Ⅱ）证明：
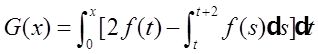
是周期为2的周期函数。
【考点】 积分函数的计算
证明：（Ⅰ）对任意实数t都有
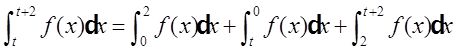
而
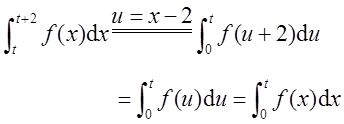
又因为
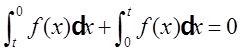
所以
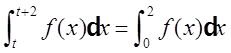
（Ⅱ）由（Ⅰ）知任意实数t都有
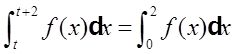
记
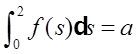
则
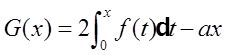
则对任意的z，有
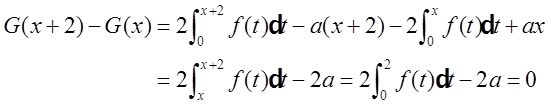
故G（x）是周期为2的周期函数。
19 （本题满分10分）
设银行存款的年利率为r＝0.05，并依年复利计算，某基金会希望通过存款A万元实现第一年提取19万元，第二年提取28万元，…，第n年提取（10＋9n）万元，并能按此规律一直提取下去，问A至少应为多少万元？
【考点】 级数的求和
解： 设A n 为用于第n年提取（10＋9n）万元的贴现值，则A n ＝（1＋r） － n （10＋9n），故
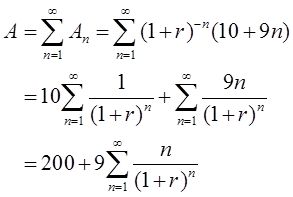
设
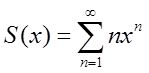
x∈（－1，1），
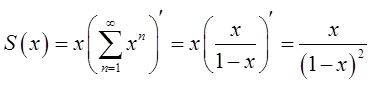
所以S[1/（1＋r）]＝S（1/1.05）＝420（万元）。故A＝200＋9×420＝3980（万元），即至少应存入3980万元。
20 （本题满分12分）
设n元线性方程组Ax＝b，其中矩阵
x＝（x 1 ，x 2 ，…，x n ） T ，b＝（1，0，…，0） T 。
（Ⅰ）证明行列式|A|＝（n＋1）a n ；
（Ⅱ）当a为何值时，该方程组有唯一解，并求x 1 ；
（Ⅲ）当a为何值时，该方程组有无穷多解，并求通解。
【考点】 行列式的计算，方程组有解的判定及其解的情况
解： （Ⅰ）由题意知
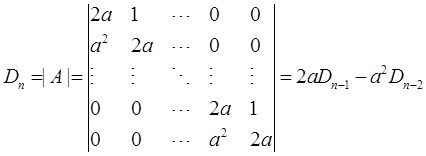
现用数学归纳法证明|A|＝（n＋1）a n ：
当n＝2时，
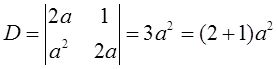
显然成立；
假设n≤k时，D k ＝（k＋1）a k ，则当n＝k＋1时，有D k ＋ 1 ＝2aD k －a 2 D k － 1 ＝2a（k＋1）a k －a 2 ka k － 1 ＝（k＋2）a k ＋ 1 。
综上可得，|A|＝（n＋1）a n 。
（Ⅱ）|A|＝（n＋1）a n ≠0，即a≠0，方程组有唯一解，设将A的第一列用b替换后所得矩阵为A 1 ，根据克莱姆法则，得x 1 ＝|A 1 |/A 1 ＝D n － 1 /[（n＋1）a n ]＝na n － 1 /[（n＋1）a n ]＝n/[（n＋1）a]。
（Ⅲ）当a＝0时，方程组有无穷多解，此时
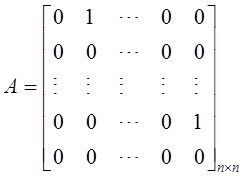
则Ax＝0的同解方程组为
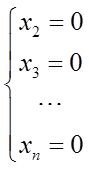
易求得Ax＝0的基础解系为（1，0，…，0） T 。又
则（0，1，…，0） T 是Ax＝b的特解，从而Ax＝b的通解为x＝k（1，0，…，0） T ＋（0，1，…，0） T ，其中k为任意常数。
21 （本题满分10分）
设A为3阶矩阵，α 1 ，α 2 为A的分别属于特征值－1，1的特征向量，向量α 3 满足Aα 3 ＝α 2 ＋α 3 。
（Ⅰ）证明：α 1 ，α 2 ，α 3 线性无关；
（Ⅱ）令P＝（α 1 ，α 2 ，α 3 ），求P － 1 AP。
【考点】 向量组的相关性判定和矩阵的运算
解： （Ⅰ）设存在数k 1 ，k 2 ，k 3 ，使得k 1 α 1 ＋k 2 α 2 ＋k 3 α 3 ＝0①。由已知条件知Aα 1 ＝－α 1 ，Aα 2 ＝α 2 。用矩阵A分别乘式①的左右两边，得－k 1 α 1 ＋k 2 α 2 ＋k 3 （α 2 ＋α 3 ）＝0②。式①－②得2k 1 α 1 －k 3 α 2 ＝0。
由于α 1 ，α 2 为A的分别属于－1，1的特征向量，所以α 1 ，α 2 线性无关，即k 1 ＝k 3 ＝0，代入①得k 2 α 2 ＝0。因为α 2 是A的特征向量，α 2 ≠0，得k 2 ＝0，即k 1 ＝k 2 ＝k 3 ＝0，所以α 1 ，α 2 ，α 3 线性无关。
（Ⅱ）由题意有
因为α 1 ，α 2 ，α 3 线性无关，所以矩阵P可逆，得
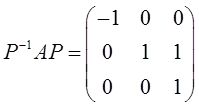
22 （本题满分11分）
设随机变量X与Y相互独立，X的概率分布为P{X＝i}＝1/3（i＝－1，0，1），Y的概率密度为
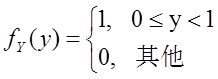
记Z＝X＋Y。
（Ⅰ）求P{Z≤1/2|X＝0}；
（Ⅱ）求Z的概率密度f Z （z）。
【考点】 求概率和概率密度函数
解： （Ⅰ）
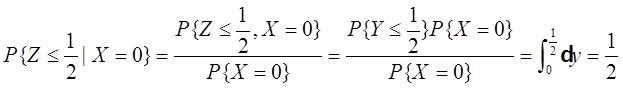
（Ⅱ）设Z的分布函数为F（z），则其值域非零时z的区间为[－1，2]。
当z＜－1时，F Z （z）＝0；
当z＞2时，F Z （z）＝1；
当－1≤z＜2时，F Z （z）＝P{Z≤z}＝P{X＋Y≤z}＝P{X＋Y≤z︱X＝－1}P{X＝－1}＋P{X＋Y≤z︱X＝0}P{X＝0}＋P{X＋Y≤z︱X＝1}P{X＝1}＝[P{Y≤z＋1}＋P{Y≤z}＋P{Y≤z－1}]/3＝[F Y （z＋1）＋F Y （z）＋F Y （z－1）]/3。
故Z的分布密度函数为
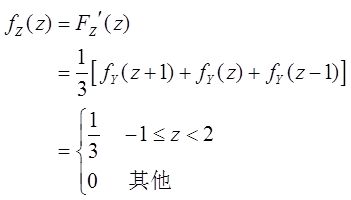
23 （本题满分11分）
设X 1 ，X 2 ，…，X n 是总体N（μ，σ 2 ）的简单随机样本，记
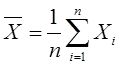
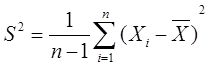
T＝ X 2 －S 2 /n
（Ⅰ）证明T是μ 2 的无偏估计量；
（Ⅱ）当μ＝0，σ＝1时，求DT。
【考点】 参数估计中的无偏估计及方差的计算
解： （Ⅰ）由题意知
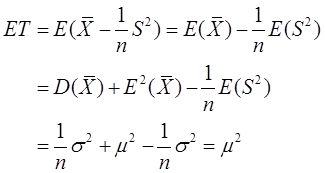
故T是μ 2 的无偏估计量。
（Ⅱ）当μ＝0，σ＝1时， X ～N（0，1/n），即有n X 2 ～χ 2 （1），（n－1）S 2 ～χ 2 （n－1），而D（χ 2 （n））＝2n。则
