





女士们,先生们:
在人类智慧发展的最初始阶段,人们就已经形成了关于空间和时间的概念,认为所有事件都发生在这个框架里。这些概念一代一代地流传了下来,没有什么本质上的改变。而且自精密科学发展以来,这些概念就被用作对这个宇宙进行数学描述的基础。伟人牛顿可能是第一位清楚地阐释了古典空间和时间概念的人,他在他的《自然哲学的数学原理》一书中写道:
绝对空间,就其本质而言,与外界任何事物都无关,永远保持相同且固定。
绝对的、真正的数学的时间,就其自身及本质而言,永远稳定地流动,与外界任何事物无关。
人们坚定不移地相信着关于时间和空间的这些古典概念的绝对正确性,以至于哲学家们总是把它们当作既定的先验事实,也没有一位科学家曾质疑过它们的正确性。
然而,就在20世纪初,有一种现象越来越明显了。用实验物理学的最精密的方法得到的一些结论,如果非要用古典时空概念来解释的话,必定会产生自相矛盾的观点。当代最出色的物理学家之一,阿尔伯特·爱因斯坦,就从这一事实中发展出了革命性的想法。他认为,除了那些传统因素外,人们没有任何理由非要认为关于时空的那些古典概念是绝对正确的。人们可以也应该要改变这些概念,以适应我们新的更加精密的实验结果。实际上,既然知道了这些古典的时空概念是建立在人类日常生活经验的基础上的,那么基于现代高度发达的实验技术建立的精密的观察方法表明了这些旧概念太粗糙、不精确,我们也不必太过惊讶。旧概念之所以可以用于日常生活以及物理发展的早期阶段,仅仅是因为它们和正确概念之间的偏差微乎其微。同样,我们也不必惊讶,现代科学探索领域的不断扩大,随之而来的是出现了一些区域,两种概念之间的偏差变得非常大,这些区域内的现象是无法用古典概念进行解释的。
对古典概念进行根本性批判的最重要的实验结果是,发现了真空中的光速代表着一切可能的物理速度的上限。这个出人意料的重要的结论主要出自美国物理学家迈克尔逊的实验。19世纪末,他努力去观察地球的运动对光传播速度的影响,令他大为吃惊并且震惊了整个科学界的是,他发现这根本没有影响,无论使用何种测量体系,也无论光源的运动如何,真空中光速一直保持不变。因此,也就没有必要去解释了,这样的一个实验结果完全反常,与我们关于运动的最基本的概念相悖。实际上,假设有一个物体在空间中快速移动,你也快速地和它进行相对运动,那个移动的物体便会以相对的更快的速度撞击到你,这个速度就是物体的速度和你移动的速度之和。反之,如果你在它之前进行同向运动,它撞击到你的速度就会减慢,相当于你和它的速度差。
同样,如果你开着车,与空中传来的声音相向而行,那么车里测出来的声速就会比你的车速快;如果声音从后面追上你的车,那么测出的声速就相应地慢了。我们把这个现象称为速度相加理论,它往往是不证自明的。
然而,最严谨的实验显示,这套速度理论在光的研究中不再适用。真空中的光速永远恒定,为每秒300 000 000米(我们通常用符号c来指代),无论观察者运动的速度有多快。
“是的,”你可能会说,“那有可能把若干个实际上可以达到的比较小的速度加起来,构成一个超光速吗?”
举个例子,假设有一辆快速行驶的火车,速度达到四分之三个光速,有一个流浪汉在火车车厢顶部同样以四分之三的光速跑着。
根据速度相加理论,那么这两个速度相加的总速度就是光速的1.5倍,那么这个在火车顶上跑的人就能够超过信号灯发射的光束。然而实际情况是,既然光速是恒定的,这是一个实验事实,而且我们实验中的速度一定小于期望值——速度并不能超过极限值c,因此可以得出结论:就算是对于较小的速度而言,古典速度相加理论也是不成立的。
关于这个问题的数学处理方式(在此我不想深入讲下去),得出了一个新的简单的公式,用于计算两个叠加运动的合成速度。
如果 v 1 和 v 2 是两个要相加的速度,那么合成速度就是:

从这个公式里可以看出,如果原来的两个速度都很小,我说的小是与光速相比,那么公式(1)中分母的第二项与整体公式相比就可以忽略不计,得到的还是古典的速度相加理论。然而,如果
v
1
和
v
2
都不小,那么结果总会比这两个速度的算术和小一些。比如,在我们火车的例子里,
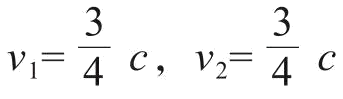 ,那么用这个公式得出的速度
,那么用这个公式得出的速度
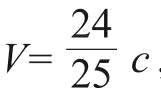 ,还是比光速小。
,还是比光速小。
在一种极端情况下,如果其中一个的原始速度为 c 时,无论另一个的速度为多少,公式①得出的速度始终为 c 。不管将多少个速度相加,我们都无法超越光速。
你可能也会想要知道,这个公式已经通过实验加以证明了,实验也真的发现两个速度的合成速度总是小于两者的算术和。
当我们认识到速度上限的存在,我们便可以开始批判古典时空概念了。首先我们要推翻的是基于古典时空概念建立的同时性概念。
当你说“开普敦煤矿爆炸的同时,火腿蛋正端上你伦敦公寓的餐桌上”,你认为自己知道自己说的意思是什么。然而现在我要告诉你,你并不知道,而且严格来讲,你说的这句话没有任何确切的含义。实际情况是,你要用什么方法来检查发生在两个不同的地方的两件事是不是同时发生的?你可能会说,两地的时钟上都显示同样的时间,那么同样的问题就来了,要如何将两个相距遥远的钟表调到同时显示相同时间呢?于是我们就回到了刚开始的问题。
既然真空中的光速不依赖于光源的运动和测量光速的系统这已经是最精确确定了的实验事实,那么接下来测量距离的方法和在不同观测站正确设置时钟的方法,应该被认为是最适当的,以及是唯一合理的方法——只要你再仔细考虑一下,就一定会同意的。
从A站发射一个光信号,B站一接收到这个光信号就立刻返回给A站。那么A站所记录的从发射信号到信号返回的时间的一半,乘上恒定的光速值,就得到了AB两站之间的距离。
如果B站收到信号的瞬间,当地的时钟正好指的是A站发射和收到信号的两个瞬时时间的中间值,那么A、B两站的时钟就可以说是校准了。在不同的观测站间采用这种方法,给我们建立了一个牢固的所希望达成的参考框架,运用这个框架,我们可以回答所有关于同时性和不同地点发生的事件的时间差的问题。
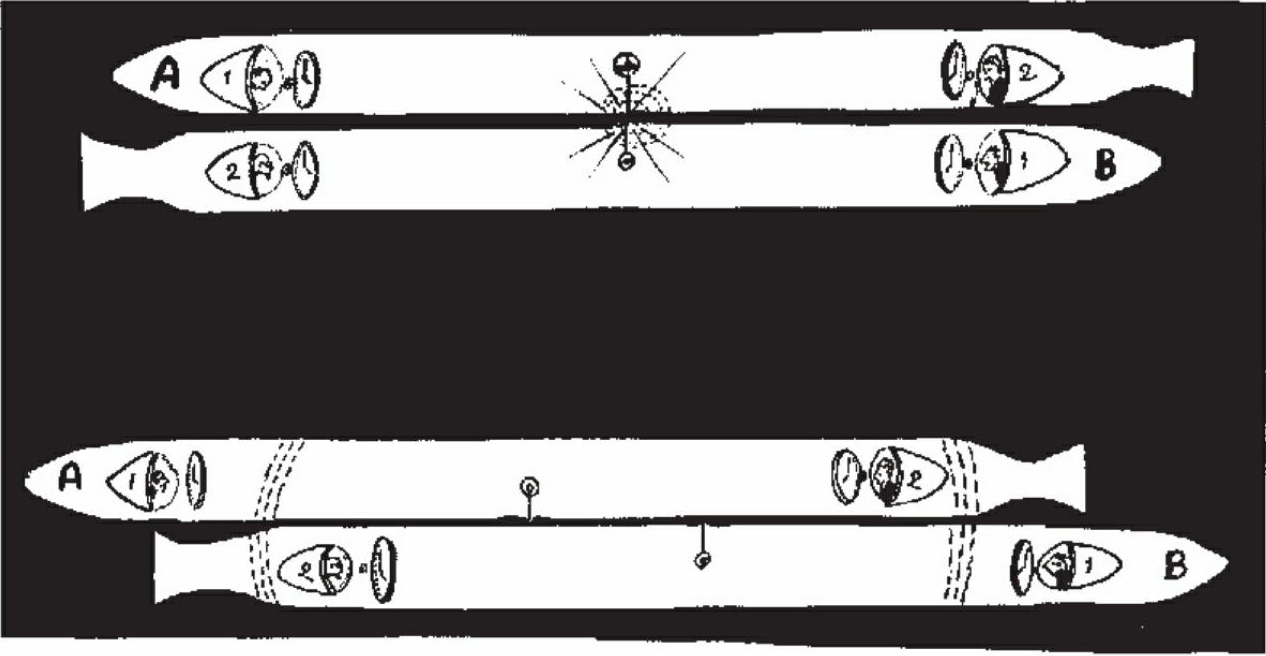
两个相反方向运动的长条火箭
但是其他参考体系里的观察者们会不会承认这些结果呢?为了回答这个问题,我们来假设一下。两个参考框架是建立在两个不同的实体上的,就假设是固定在以相同恒定速度朝反方向飞行的两个长条太空火箭上,那么我们就来看一看这两个参考框架是如何校准的。假设各有两对观察者分别固定在每个火箭的头部和尾部,首先要做的就是将他们的表校准。每一对观察者可以在火箭上将上述方法稍微调整一下,从火箭中点(用量尺测量好)发射光信号,当光信号发射之后到达两端的同时,两对观察者将表调到零点。这样,每一对观察者都根据前面的规定,在自己的体系中建立了同时性标准。当然,从他们的角度将自己的表对“准”了。
现在他们决定看一看自己火箭上的时间读数是不是和对方火箭上的一样。比如,当身处两个不同火箭的观察者擦身而过的时候,他们的手表是不是指向同一时间?可以用以下方法来检测:他们在每个火箭的几何中点上安装两个带电的导体,这样,当两个火箭擦身而过的时候,导体之间碰撞出火花,就在这个瞬间每个火箭的中点同时向两端发射光信号。当光信号(以恒定的速度)朝观察者移动的时候,火箭已经改变了它们的相对位置,2A和2B两个观察者将比1A和1B两个观察者更接近光源。
很显然,当2A接收到光信号的时候,1B还没有接收到,所以还需要额外的时间才能收到信号。因此,即使用这样的方法1B在信号一到达的时候就把手表拨零,2A还是坚持认为他的表慢了。
同样地,其他观察者也是这样。1A会得出结论说2B的手表提前了,因为2B在其之前收到光信号。既然,根据他们自己的同时性定义,他们的手表都校准了,火箭A上的观察者们会认为自己的表与火箭B上的观察者们的表有时间差。不过我们不要忘记,火箭B上的观察者们也会因为同样的原因而以为自己的表是校准的,而声称与火箭A观察者们的表有时间差的存在。
既然这两个火箭是完全等价的,那么解决两组观察者之间的争论的方法,只有说这两组观察者,从他们各自的角度来看都是对的。但至于谁是“绝对”正确的问题,没有任何物理意义。
我生怕你们听我讲这些长篇大论听得太累了,不过你要是仔细地从头顺下来的话,你就很清楚,一旦我们采纳上述的时—空测量法,绝对同时性的概念就会消失,在一个参考体系中被认为是同时发生在不同地方的两件事,在另外一个体系看来就会被分割成有时间间隔的两个事件。
这种观点一开始听起来极度不正常,但如果我说,你在火车上吃晚餐,你在餐车的同一个位置吃着甜点喝着汤,却是在铁轨上相距很远的两个点上吃的,那么现在你还是觉得不正常吗?不过,你在火车上吃晚餐这个例子可以总结为一点,在一个体系的同一点的不同时间发生的两件事,可能会在另外一个体系中变成有一定空间间隔的两件事。
如果把这种“平常”的观点和之前那个“反常”的观点做比较,你会发现这两个观点是完全对称的,仅仅只要把“时间”和“空间”两个词对调一下,一种说法就变成了另外一种说法。
爱因斯坦的整体观点就是:在古典物理学中,时间被看作完全独立于空间和运动“稳定地流动,与外界任何事物无关”(牛顿),在新物理学中,时间和空间是紧密联系的,它们代表的是一个均质的“空间—时间连续统”的两个不同的截面。我们所能观察到的事件都发生在这样一个连续统里。
将这个四维的连续统分裂成一个三维的空间和一个一维的时间纯粹是很武断的,要取决于观察现象时所处的体系。
在一个体系里观察,在空间里被距离 l ,在时间上被间隔 t 分隔成了两个事件,而在另外一个体系里,将会被另外的距离 l ' 和另外的间隔 t ' 分隔成另外的两个事件。所以,从一定意义上来讲,我们可以说把空间转换成了时间,反之亦然。同样也不难看出,为什么从时间转换成空间,就像火车上的晚餐这个例子一样,对我们来说是普通的概念,而将空间转换成时间,形成了同时性的相对性,这对我们来说就很反常了。我想说的一个点是,如果我们测量距离使用的是“厘米”,那么相对应的时间单位就不应该是传统的“秒”,而是“合理的时间单位”,即光信号走过1厘米所需要的时间间隔0.000 000 000 03秒。
因此,在我们日常经验的范围内,从空间间隔转换成时间间隔所产生的结果实际上是无法观察到的,这似乎佐证了认为时间是绝对独立和亘古不变的古典观点。
然而,在研究极高速运动,如发射性物质所发射出的电子的运动或者原子内部电子的运动时,在这些情况下某一时间间隔内走过的距离与用合理时间单位所表示的时间属于同一个数量级,这就必定会遇到我们上面讲到的两个效应。这时相对论就变得至关重要了。甚至在相对较低速的区域里,比如我们太阳系的行星运动,用极度精密的天文观测仪器也可以观察到相对论效应;不过想要观察相对论效应,就需要测出每年行星运动总共只有几分之一弧秒的变化。
我已经很尽力地解释给你们听了,对古典空间和时间概念的批判最后会得到一个结论,那就是空间间隔可以部分地转换成时间间隔,时间间隔也可以部分地转换成空间间隔。这也意味着在不同的运动系统中测量一个既定的距离或者时间,会得到不同的数值。
对于这个问题进行一个相对比较简单的数学分析,不过我在讲座中不会深入,可以得出一个关于数值变化的明确的公式。任何一个长度为 l 的物体,以 v 的速度相对于观察者运动,它的长度都会缩短,缩短的数值取决于它的速度,观察者所测到的速度是:

类似地,一个过程需要花时间 t ,当从一个做相对运动的体系观察它时,所花的时间是 t ',如公式(3)所示。

这就是相对论中著名的“尺缩(空间缩短)效应”和“钟慢(时间延长)效应”。
一般情况下,当 v 比 c 小很多的时候,效应会很细微。但如果从一个运动的体系中,速度足够大时会观察到,长度会变得非常短,而时间间隔会变得非常长。
我希望大家不要忘记,这两个效应是完全对称的体系,所以高速行驶的火车上的乘客会很好奇为什么外面站着不动的人们看上去那么瘦,动得那么慢,而站着不动的人们看着火车上的乘客们也会很好奇。
另一个重要的点是,运动物体的最大可能速度与它的质量有关。
根据一般力学原理,物体的质量决定了使物体开始运动或者使运动物体加速的难度。物体质量越大,使物体增加某一数量的难度也就越大。
任何物体在任何情况下都不能超过光速,这一事实直接让我们得出了一个结论:当物体的速度趋近于光速的时候,它加速遇到的阻力,换句话说,它的质量,将会无限增大。数学分析得出了计算这个关系的公式,和公式(2)(3)类似。如果 m 0 代表的是速度非常小的时候的质量,那么其质量 m 和速度 v 的关系就是:

当 v 趋近于 c 的时候,进一步加速遇到的阻力将会变得无限大。
质量发生相对论性变化的效应很容易通过实验在高速运动的粒子上观察到。例如,放射性物质发射出的电子的质量(其速度接近光速的99%)比静止状态的粒子的质量大若干倍,而构成宇宙射线的电子常常以99.98%光速的速度运动,其质量更是静止状态下电子质量的一千倍。对于这么大的速度,古典物理学变得丝毫不再适用了,我们进入了相对论纯理论领域。