




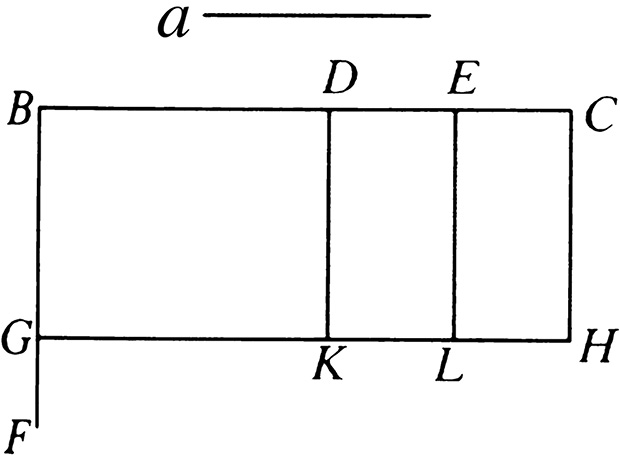
设: a 、 BC 是两条线段,用点 D 、 E 分线段 BC 。
那么可以说:由 a 、 BC 所夹的矩形等于由 a 、 BD 与 a 、 DE 以及 a 、 EC 分别所夹的矩形的和。
因为:从 B 作 BF 和 BC 成直角,[I. 11]
取 BG 等于 a ,[I. 3]
过 G 作 GH 平行于 BC ,[I. 31]
并经过点 D 、 E 、 C ,作 DK 、 EL 、 CH 平行于 BG 。
那么 BH 等于 BK 、 DL 、 EH 的和。
BH 是矩形 a 、 BC ,由于它是由 GB 和 BC 围成的,并且 BG 等于 a ,
BK 是矩形 a 、 BD ,由于它是由 GB 、 BD 围成的,并且 BG 等于 a ,
又因: DL 是矩形 a 、 DE ,由于 DK 是 BG 并且等于 a ,[I. 34]
同理可证: EH 也是矩形 a 、 EC ,
所以:矩形 a 、 BC 等于矩形 a 、 BD 与矩形 a 、 DE 及矩形 a 、 EC 的和。
证完。
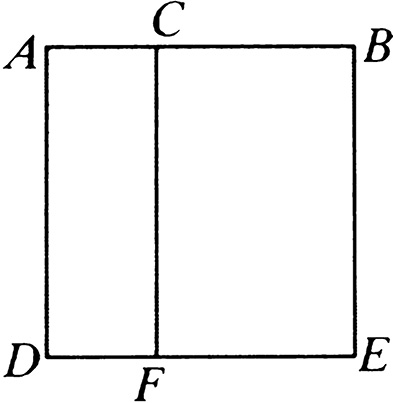
设:任意两分线段 AB 于点 C 。
那么可以说:由 AB 、 BC 所夹的矩形与 BA 、 AC 所夹的矩形的和等于 AB 上的正方形。
设:在 AB 上作的正方形为 ADEB 。[I. 46]
经过点 C 作 CF 平行于 AD 或 BE 。[I. 31]
那么 AE 等于 AF 与 CE 的和。
因为: AE 是 AB 上的正方形,
AF 是由 BA 、 AC 围成的矩形,因为它是由 DA 、 AC 围成,且 AD 等于 AB ,
又因: BE 等于 AB ,
因此: CE 是由 AB 、 BC 围成的矩形,
所以:矩形 BA 、 AC 与矩形 AB 、 BC 的和等于 AB 上的正方形。
证完。
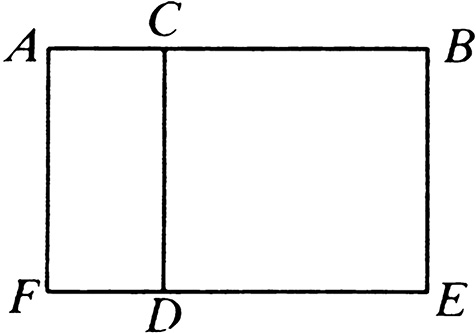
设:任意两分线段 AB 于 C 。
那么可以说:由 AB 、 BC 围成的矩形等于由 AC 、 CB 围成的矩形与 BC 上的正方形的和。
在 CB 上作正方形 CDEB ,[I. 46]
延长 ED 至 F ,过 A 作 AF 平行于 CD 或者 BE 。[I. 31]
那么 AE 等于 AD 与 CE 的和。
因为: AE 是由 AB 、 BC 所围成的矩形,这是因为它是由 AB 、 BE 所围成的,且 BE 等于 BC ,
又因: DC 等于 CB ,并且 DB 是 CB 上的正方形,
因此: AD 是矩形 AC 、 CB ,
所以: AB 、 BE 围成的矩形等于由 AC 、 CD 围成的矩形与 BC 上的正方形的和。
证完。
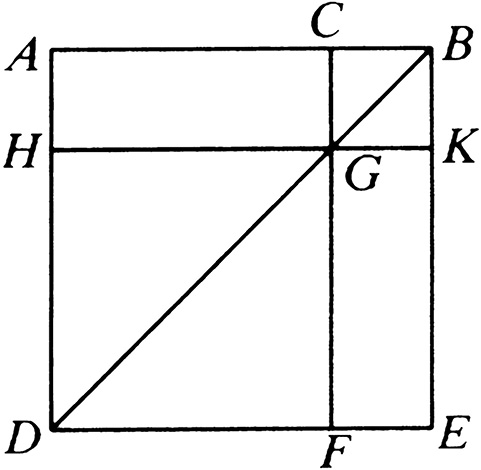
设:任意线段 AB 分于 C 。
那么可以说: AB 上的正方形等于 AC 及 CB 上的正方形的和,加上 AC 、 CB 围成的矩形的二倍。
让 AB 上所作的正方形为 ADEB ,[I. 46]
连接 BD ,过点 C 作 CF 平行于 AD 或 EB ,过点 G 作 HK 平行于 AB 或 DE 。[I. 31]
因为: CF 平行于 AD ,且 BD 与 CF 、 AD 都相交,那么同位角 CGB 、 ADB 相等,[I. 29]
且因边 BA 等于边 AD ,
因此:角 ADB 等于角 ABD ,[I. 5]
所以:角 CGB 等于角 GBC ,边 BC 等于边 CG 。[I. 6]
因为: CB 等于 GK , CG 等于 KB ,[I. 34]
所以: GK 等于 KB ,
所以: CGKB 是等边的。
然后,又可证明 CGKB 是直角。
因为: CG 平行于 BK 。角 KBC 、角 GCB 的和等于两直角,[I. 29]
又因:角 KBC 是直角,
所以:角 BCG 也是直角,对角 CGK 及角 GKB 同样是直角,[I. 34]
所以: CGKB 四个角都是直角,由于已经证明它是等边,因此它是正方形,从而推出 CGKB 是作在 CB 上的正方形。
同理可证: HF 也是正方形,它是作在 HG 上的,也就是作在 AC 上的正方形,[I. 34]
所以:正方形 HF 、 KC 是作在 AC 、 CB 上的正方形。
因为: AG 等于 GE ,并且 AG 是矩形 AC 、 CB ,且 GC 等于 CB ,
所以: GE 等于矩形 AC 、 CB ,
所以: AG 、 GE 的和等于矩形 AC 、 CB 的二倍。
因为:正方形 HF , CK 的和等于 AC 、 CB 上的正方形的和,
所以:四个面 HF 、 CK 、 AG 、 GE 等于 AC 、 CB 上的正方形加上 AC 、 CB 围成的矩形的二倍。
又因为: HF 、 CK 、 AG 、 GE 的和是整体 ADEB ,它就是 AB 上的正方形,
所以: AB 上的正方形等于 AC 、 CB 上的正方形的和加上 AC 、 CB 围成的矩形的二倍。
证完。
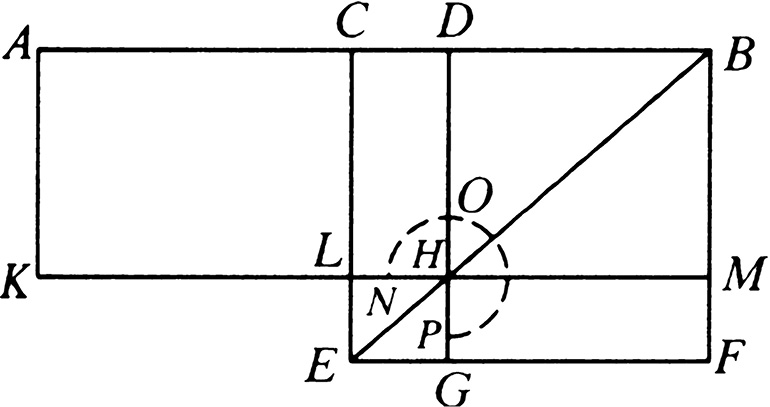
设:由点 C 将线段 AB 分成相等的两线段,用点 D 将线段 AB 分成不相等的两线段。
那么可以说: AD 、 DB 围成的矩形加上 CD 上的正方形的和等于 CB 上的正方形。
设: CEFB 是作在 CB 上的正方形。[I. 46]
连接 BE ,过 D 作 DG 平行于 CE 或 BF ,过 H 作 KM 平行于 AB 或 EF ,再过 A 作 AK 平行于 CL 或 BM ,[I. 31]
那么:补形 CH 等于补形 HF 。[I. 43]
将 DM 加在以上两边,那么整体 CM 等于整体 DF 。
因为: AC 等于 CB ,
所以: CM 等于 AL ,[I. 36]
AL 等于 DF 。
将 CH 加在以上各边,那么整个 AH 等于拐尺形 N OP 。
因为: DH 等于 DB ,
所以:拐尺形 NOP 等于矩形 AD 、 DB 。
LG 等于 CD 上的正方形,将它加在以上各边,
那么:拐尺形 NOP 与 LG 的和等于 AD 、 DB 围成的矩形与 CD 上的正方形的和。
又因:拐尺形 NOP 与 LG 的和是 CB 上的整体正方形 CE FB ,
所以: AD 、 DB 围成的矩形与 CD 上的正方形的和等于 CB 上的正方形。
证完。
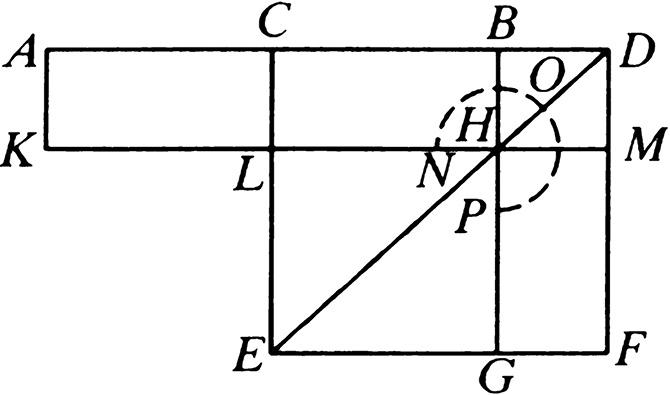
设:点 C 平分线段 AB ,在同一直线上加上线段 BD 。
那么可以说: AD 、 DB 围成的矩形与 CB 上的正方形的和等于 CD 上的正方形。
设: CEFD 是在 CD 上所作的正方形。[I. 46]
连接 DE ,过点 B 作 BG 平行于 EC 或 DF ,过点 H 作 KM 平行于 AB 或 EF ,过点 A 作 AK 平行于 CL 或 DM 。[I. 31]
因为: AC 等于 CB , AL 等于 CH ,[I. 36]
又因: CH 等于 HF ,[I. 43]
所以: AL 等于 HF 。
将 CM 加在各边,
那么:整个 AM 等于拐尺形 N OP 。
又因: AM 是由 AD 、 DB 围成的矩形,且 DM 等于 DB ,
所以:拐尺形 NOP 等于矩形 AD 、 DB 。
将 LG 加在以上各边,等于 BC 上的正方形,
所以: AD 、 DB 围成的矩形与 CB 上的正方形的和等于拐尺形 NOP 与 LG 的和。
又因:拐尺形 NOP 与 LG 是作在 CD 上的整体正方形 CE FD ,
所以:由 AD 、 DB 围成的矩形与 CB 上的正方形的和等于 CD 上的正方形。
证完。
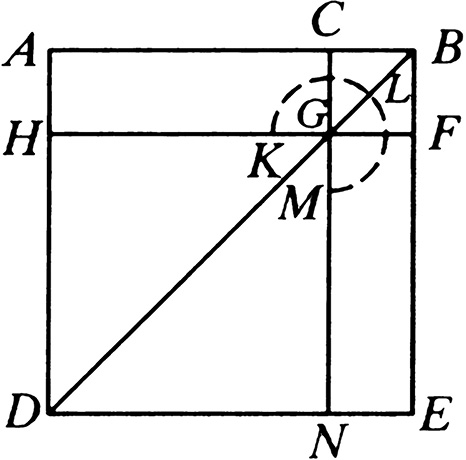
设:线段 AB 被点 C 任意分为两段。
那么可以说: AB 、 BC 上的正方形的和等于 AB 、 BC 围成的矩形的二倍与 CA 上的正方形的和。
设:在 AB 上所作的正方形为 ADEB ,[I. 46]
并且图已作。[I. 46]
因为: AG 等于 GE ,[I. 43]
将 CF 加在以上各边,那么整体 AF 等于整体 CE ,因此 AF 、 CE 的和是 AF 的二倍,
因为: AF 、 CE 的和是拐尺形 KLM 与正方形 CF 的和,
所以:拐尺形 KLM 与正方形 CF 的和是 AF 的二倍。
又因:矩形 AB 、 BC 的二倍也是 AF 的二倍,且 BF 等于 BC ,
所以:拐尺形 KLM 与正方形 CF 的和等于二倍的矩形 AB 、 BC 。
将 DG 加在以上各边, DG 是 AC 上的正方形,
所以:拐尺形 KLM 与正方形 BG 、 GD 的和,等于 AB 、 BC 围成的矩形的二倍与 AC 上的正方形的和。
因为:拐尺形 KLM 与正方形 BG 、 GD 的和是整体 ADEB 与 CF 的和,它们是在 AB 、 BC 上所作的正方形,
所以: AB 、 BC 上的正方形的和等于 AB 、 BC 围成的矩形的二倍与 AC 上的正方形的和。
证完。
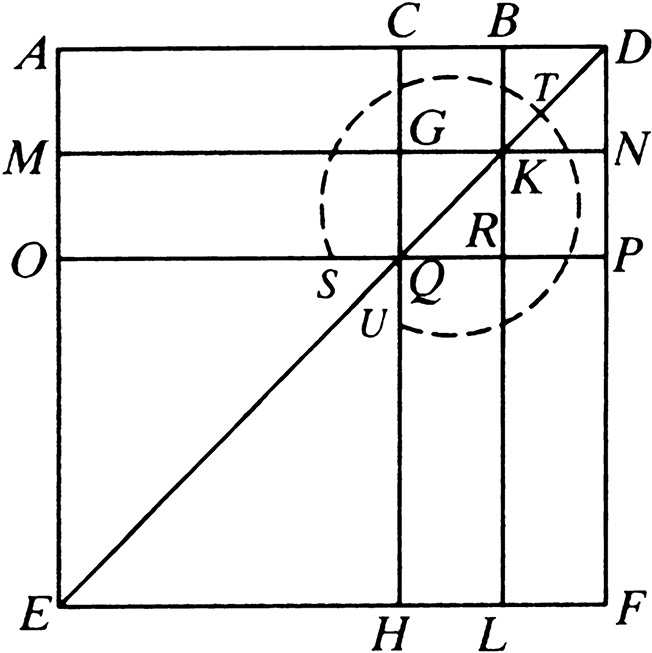
设:线段 AB 分于 C 。
那么可以说: AB 、 BC 所夹的矩形的四倍与 AC 上的正方形的和,等于 AB 与 BC 合成直线上的正方形。
延长线段 AB 至 D ,使 BD 等于 CB ,假设画在 AD 上的正方形是 AEFD ,并且作这样两个图。
因为: CB 等于 BD ,且 CB 等于 GK ,并且 BD 等于 KN ,
所以: GK 等于 KN 。
同理可证: QR 等于 RP 。
又因: BC 等于 BD , GK 等于 KN ,
所以: CK 等于 KD , GR 等于 RN 。[I. 36]
又因: CK 和 RN 是平行四边形 CP 的补形,
所以: CK 等于 RN ,[I. 43]
所以: KD 等于 GR ,四个面 DK 、 CK 、 GR 、 RN 都彼此相等,
因此:这四个面的和是 CK 的四倍。
又因: CB 等于 BD ,
BD 等于 BK ,也是 CG ,并且 CB 等于 GK ,也是 GQ ,故 CG 等于 GQ 。
并且 CG 等于 GQ ,并且 QR 等于 RP ,
AG 等于 MQ , QL 等于 RF ,[I. 36]
又因: MQ 和 QL 是平行四边形 ML 的补形,因此 MQ 等于 QL ,[I. 43]
所以: AG 等于 RF ,
故,四个面 AG 、 MQ 、 QL 、 RF 彼此相等,
所以:这四个面的和是 AG 的四倍。
因为:四个面 CK 、 KD 、 GR 、 RN 已被证明它们的和是 CK 的四倍,
所以:这八个面构成的拐尺形 STU 是 AK 的四倍。
又因: BK 等于 BD ,
所以: AK 是矩形 AB 、 BD ,故四倍的矩形 AB 、 BD 是 AK 的四倍。
因为:拐尺形 STU 已经被证明了是 AK 的四倍,
所以:矩形 AB 、 BD 的四倍等于拐尺形 S TU 。
将 OH 加在以上各边,等于 AC 上的正方形,
所以:矩形 AB 、 BD 的四倍与 AC 上的正方形的和等于拐尺形 STU 与 OH 的和。
又因:拐尺形 STU 与 OH 的和等于作在 AD 上的整体正方形 AE FD ,
所以:四倍的矩形 AB 、 BD 与 AC 上的正方形的和等于 AD 上的正方形。
又因: BD 等于 BC ,
所以:四倍的矩形 AB 、 BC 与 AC 上的正方形的和等于 AD 上的正方形,也就是 AB 与 BC 合成直线上的正方形。
证完。
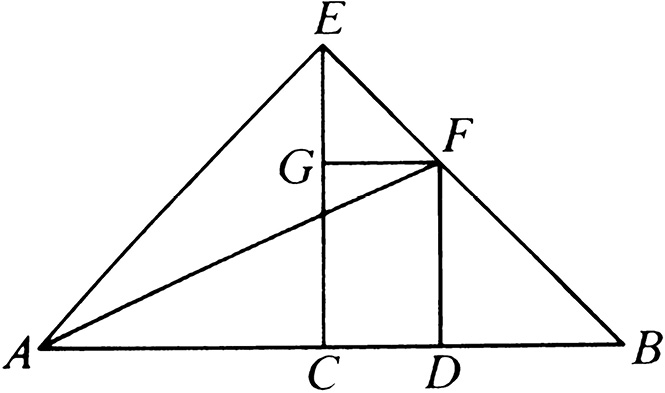
设:线段 AB 被点 C 分成相等的线段,又被点 D 分成不相等的线段。
那么可以说: AD 、 DB 上的正方形的和等于 AC 、 CD 上的正方形的和的二倍。
因为:从 AB 上的点 C 作 CE 和 AB 成直角,并且它与 AC 或 CB 相等。连接 EA 、 EB 。经过点 D 作 DF 平行于 EC ,并且过 F 作 FG 平行于 AB ,连接 AF ,
并且 AC 等于 CE ,角 EAC 等于角 A EC ,
又因:在点 C 的角是直角,其余两个角 EAC 、 AEC 的和等于直角,[I. 32]
且它们又相等,
所以:角 CEA 、 CAE 各是直角的一半。
同理可证:角 CEB 、 EBC 各是直角的一半,
所以:整体角 AEB 是直角。
又因: GEF 是直角的一半,角 EGF 是直角,由于它与角 ECB 是同位角,[I. 29]
剩下的角 EFG 是直角的一半,[I. 32]
所以:角 GEF 等于角 E FG ,
由此,边 EG 等于边 GF 。[I. 6]
又因:在点 B 处的角是直角的一半,并且因为角 FDB 与角 ECB 是同位角,所以角 FDB 是直角,[I. 29]
剩下的角 BFD 是直角的一半,[I. 32]
所以:在点 B 处的角等于角 D FB ,
由此,边 FD 等于边 DB 。
因为: AC 等于 CE , AC 上的正方形等于 CE 上的正方形,
所以: AC 、 CE 上的正方形的和是 AC 上的正方形的二倍。
又因:角 ACE 是直角,所以 EA 上的正方形等于 AC 、 CE 上的正方形的和,[I. 47]
所以: EA 上的正方形是 AC 上的正方形的二倍。
又因: EG 等于 GF ; EG 上的正方形等于 GF 上的正方形,
所以: EG 、 GF 上的正方形的和等于 GF 上的正方形的二倍。
又因: EF 上的正方形等于 EG 、 GF 上的正方形的和,
所以: EF 上的正方形是 GF 上的正方形的二倍。
又因: GF 等于 CD ,[I. 34]
所以: EF 上的正方形是 CD 上的正方形的二倍。
因为: EA 上的正方形也是 AC 上的正方形的二倍,
所以: AE 、 EF 上的正方形的和是 AC 、 CD 上的正方形的和的二倍。
又因:角 AEF 是直角,
所以: AF 上的正方形等于 AE 、 EF 上的正方形的和,[I. 47]
所以: AF 上的正方形是 AC 、 CD 上的正方形的和的二倍。
因为:在点 D 的角是直角,
所以: AD 、 DF 上的正方形的和等于 AF 上的正方形,[I. 47]
所以: AD 、 DF 上的正方形的和是 AC 、 CD 上的正方形的和的二倍。
又因: DF 等于 DB ,
所以: AD 、 DB 上的正方形的和等于 AC 、 CD 上的正方形的和的二倍。
证完。
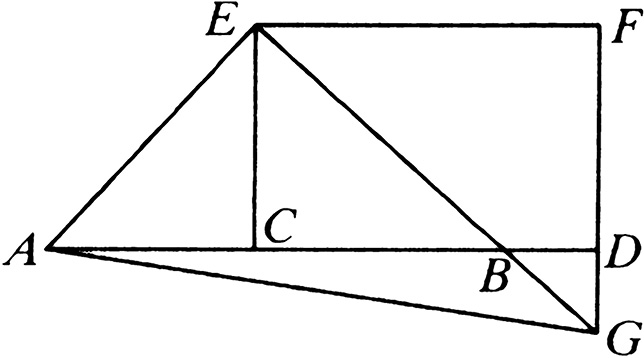
用点 C 将线段 AB 二等分,并在同一直线上给 AB 添上 BD 。
那么可以说: AD 、 DB 上的正方形的和等于 AC 、 CD 上的正方形的和的二倍。
设: CE 在 C 点和 AB 成直角,[I. 11]
让它等于 AC 或 CB 。[I. 3]
连接 EA 、 EB ,过点 E 作 EF 平行于 AD ,过点 D 作 FD 平行于 EC 。[I. 31]
因为:直线 EF 和平行线 EC 、 FD 都相交,角 CEF 、 EFD 的和等于两直角,[I. 29]
所以:角 FEB 、 EFD 的和小于两直角。
又因:直线在小于两直角的这一侧经延长后相交,[I. 公设5]
所以:若在同方向 B 、 D 延长 EB 、 FD 定相交。
设:其交点为 G ,连接 AG 。
因为: AC 等于 CE ,角 EAC 等于角 AEC ,[I. 5]
在点 C 是直角,
所以:角 EAC 、 AEC 各是直角的一半。[I. 32]
同理可证:角 CEB 、 EBC 各是直角的一半,
因此:角 AEB 是直角。
又因:角 EBC 是直角的一半,角 DBG 也是直角一半,[I. 15]
并且角 BDG 与角 DCE 相等,且它们是错角,因此:角 BDG 也是直角,[I. 29]
所以:剩下的角 DGB 是直角的一半,[I. 32]
故,角 DGB 等于角 D BG ,
所以:边 BD 等于边 GD 。[I. 6]
又因:角 EGF 等于在点 C 处的对角,故角 EGF 是直角的一半,且在点 F 处的是直角,[I. 34]
剩下的角 EFC 是直角的一半,[I. 32]
所以:角 EGF 等于角 F EG ,
边 GF 等于 EF 。
因为: EC 上的正方形等于 CA 上的正方形; EC 、 CA 上的正方形的和是 CA 上的正方形的二倍,
又因: EA 上的正方形等于 EC 、 CA 上的正方形的和,[I. 47]
所以: EA 上的正方形是 AC 上的正方形的二倍。[公理1]
因为: FG 等于 EF 、 FG 上的正方形等于 FE 上的正方形,
所以: GF 、 FE 上的正方形的和是 EF 上的正方形的二倍。
又因: EG 上的正方形等于 GF 、 FE 上的正方形的和,[I. 47]
所以:在 EG 上的正方形是在 EF 上的正方形的二倍, EF 等于 CD ,[I. 34]
所以: EG 上的正方形是 CD 上的正方形的二倍。
又因:已证 EA 上的正方形是 AC 上的正方形的二倍,
所以: AE 、 EG 上的正方形的和是 AC 、 CD 上的正方形的和的二倍。
又因:在 AG 上的正方形等于 AE 、 EG 上的正方形的和,[I. 47]
所以: AG 上的正方形是 AC 、 CD 上的正方形的和的二倍。
因为: AD 、 DG 上的正方形的和等于 AG 上的正方形,[I. 47]
所以: AD 、 DG 上的正方形的和是 AC 、 CD 上的正方形的和的二倍,
又因: DG 等于 DB ,
所以: AD 、 DB 上的正方形的和是 AC 、 CD 上的正方形的和的二倍。
证完。
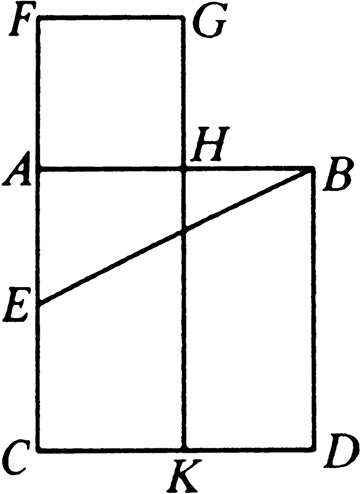
设:将已知线段 AB 分成两段,让它和一小线段所夹的矩形等于另一小线段上的正方形。
设:在 AB 上作正方形 ABDC 。[I. 46]
将 AC 二等分于点 E ,连接 BE ,延长 CA 到 F ,取 EF 等于 BE 。
设: FH 是作在 AF 上的正方形,延长 GH 至 K 。
那么可以说: H 就是 AB 上所要求作的点,它让 AB 、 BH 所夹的矩形等于 AH 上的正方形。
因为:线段 AC 被点 E 平分,并给它加上 FA ,
CF 、 FA 所夹的矩形与 AE 上的正方形的和等于 EF 上的正方形,[II. 6]
又因: EF 等于 EB ,
所以:矩形 CF 、 FA 与 AE 上的正方形的和等于 EB 上的正方形。
因为:在点 A 的角是直角,
所以: BA 、 AE 上的正方形的和等于 EB 上的正方形,[I. 47]
所以:矩形 CF 、 FA 与 AE 上的正方形的和等于 BA 、 AE 上的正方形的和。
将上面两边各减去 AE 上的正方形,
那么:剩下的矩形 CF 、 FA 等于 AB 上的正方形。
矩形 CF 、 FA 的和是 FK ,由于 AF 等于 FG ,且 AB 上的正方形是 AD ,
所以: FK 等于 AD 。
将上面两边各减去 AK ,余下的部分 FH 等于 HD 。
又因: HD 是矩形 AB 、 BH ,又因为 AB 等于 BD ,并且 FH 是 AH 上的正方形,
所以:由 AB 、 BH 围成的矩形等于 HA 上的正方形,
所以:点 H 分已知的线段 AB ,由 AB 、 BH 围成的矩形等于 HA 上的正方形。
作完。
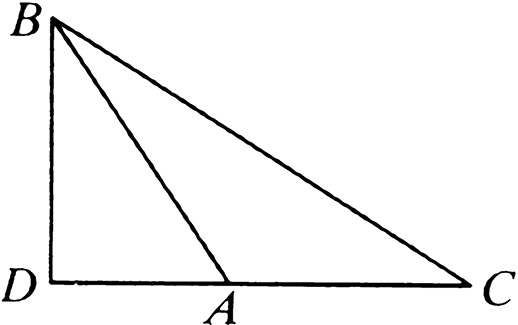
设:在 ABC 是钝角三角形,角 BAC 为钝角。由点 B 作 BD 垂直于 CA ,交延长线于点 D 。
那么可以说: BC 上的正方形比 BA 、 AC 上的正方形的和还大 CA 、 AD 围成矩形的二倍。
因为:点 A 任意分线段 CD , CD 上的正方形等于 CA 、 AD 上的正方形加上 CA 、 AD 所夹的矩形的二倍,[II. 4]
将 DB 上的正方形加在以上各边,
所以: CD 、 DB 上的正方形的和等于 CA 、 AD 、 DB 上的正方形的和加上矩形 CA 、 AD 的二倍。
又因:在点 D 的角都是直角,因此: CB 上的正方形等于 CD 、 DB 上的正方形的和,[I. 47]
且 AB 上的正方形等于 AD 、 DB 上的正方形的和,[I. 47]
所以: CB 上的正方形等于 CA 、 AB 上的正方形的和加上 CA 、 AD 围成的矩形的二倍,
所以: CB 上的正方形比 CA 、 AB 上的正方形的和还大 CA 、 AD 围成的矩形的二倍。
证完。
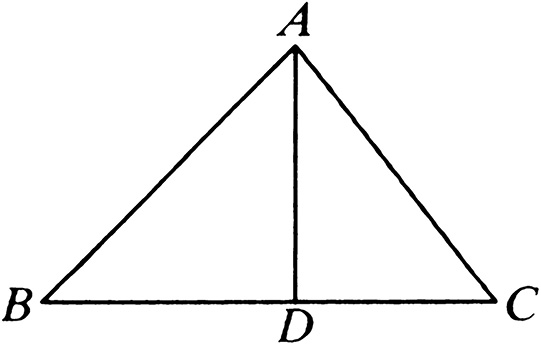
设: ABC 是锐角三角形,点 B 处的角为锐角,并且设 AD 是由点 A 向 BC 所作的垂线。
那么可以说: AC 上的正方形比 CB 、 BA 上的正方形的和小 CB 、 BD 围成的矩形的二倍。
因为: CB 任意分割于点 D ; CB 、 BD 上的正方形的和等于由 CB 、 BD 围成矩形的二倍与 DC 上的正方形的和,[II. 7]
将 DA 上的正方形加在以上各边,
那么: CB 、 BD 、 DA 上的正方形的和等于 CB 、 BD 围成的矩形的二倍加上 AD 、 DC 上的正方形的和。
因为:在 D 处的角都是直角,因此: AB 上的正方形等于 BD 、 DA 上的正方形的和,[I. 47]
并且, AC 上的正方形等于 AD 、 DC 上的正方形的和,因此: CB 、 BA 上的正方形的和等于 AC 上的正方形加上二倍的矩形 CB 、 BD ,
所以: AC 上的正方形只能比 CB 、 BA 上的正方形的和小 CB 、 BD 所夹的矩形的二倍。
证完。
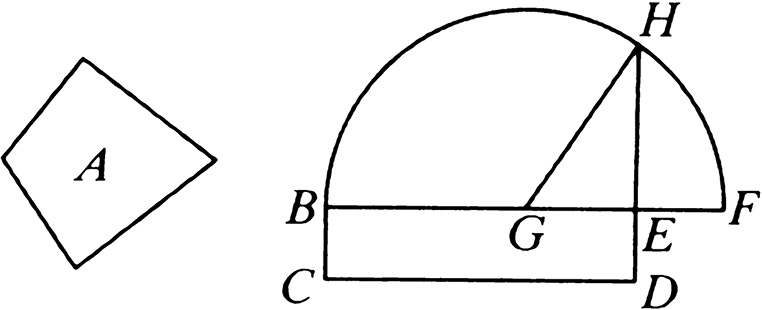
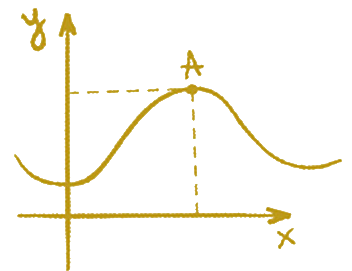
设:已知直线形 A ,作一个等于直线形面积 A 的正方形。
先设:作了一个等于直线形 A 的矩形 BD 。[I. 45]
若 BE 等于 ED ,那么因为正方形 BD 等于直线形 A ,作图完毕。
如果 BE 不等于 ED ,也就是线段 BE 、 ED 中有一条较大。
再设: BE 较大,且延长至点 F 。
设 EF 等于 ED ,且 BF 被二等分于点 G 。
以 G 为圆心,以 GB 、 GF 中的一个为距离画半圆 B HF 。
将 DE 延长至 H ,连接 GH 。
因为:线段 BF 被点 G 二等分,被点 E 分为不相等的两段,
且由 BE 、 EF 围成的矩形与 EG 上的正方形的和等于 GF 上的正方形,[II. 5]
又因: GF 等于 GH ,
所以:矩形 BE 、 EF 与 GE 上的正方形的和等于 GH 上的正方形。
又因: HE 、 EG 上的正方形的和等于 GH 上的正方形,[I. 47]
所以:矩形 BE 、 EF 加上 GE 上的正方形等于 HE 、 EG 上的正方形的和。
以上各边减去 GE 上的正方形,
那么:剩下的矩形 BE 、 EF 等于 EH 上的正方形。
因为: EF 等于 ED ,所以:矩形 BE 、 EF 是 BD ,
所以:平行四边形 BD 等于 HE 上的正方形。
又因: BD 等于直线形 A ,
所以:直线形 A 等于在 EH 上作的正方形,
所以:在 EH 上作了等于已知直线形 A 的正方形。
作完。