





由于大面积均匀透明材料的制造困难,透射元件的吸收和色散,以及大型透镜边缘支承引起的镜体变形等问题,光学天文望远镜主要采用反射式光学系统。反射式光学系统也广泛应用于射电及其他频段的天文望远镜中。在反射望远镜系统中,焦点位置可以分为主焦点、牛顿焦点、卡塞格林焦点、耐施密斯焦点及折轴焦点等系统。这些不同的焦点系统在光路、焦比、像差和镜面位置上均有各自的特点,对此本节将分别予以介绍。
只有一个反射面的主焦(prime)点系统是反射式望远镜最基本的光学系统(见图1.22(a))。根据圆锥曲线的光学性质,当主镜为旋转抛物面时,平行于抛物面轴线的光线将等光程地会聚于抛物面的焦点上,这时的星光在几何光学意义上成完善像。传统的主焦点系统的焦比通常为 F /1到 F /5,大的焦比会使镜筒增长,从而增大望远镜的造价。为了进一步增大望远镜的口径,新一代的天文望远镜将采用 F /0.5到 F /1的主焦比。在主焦系统理想的像面上没有球差,轴外彗差是主焦系统的主要像差,彗差值为3 ω /(16 F 2 ),这里ω为半视场角, F 为主镜焦比,彗差和半视场角所用的角度单位相同。主焦系统中像散和场曲与视场角的平方成正比,当视场角大于4度时,像散和场曲才会成为主要像差。主焦系统的可用视场很小,一般需要设置像场改正镜以增大视场。在天文望远镜中主焦系统主要用于成像工作。主焦系统的主要优点是光能损失少,但是由于主焦位置处在镜筒前端的入射光路中,因此焦点不易接近,不能装置较大的终端设备。
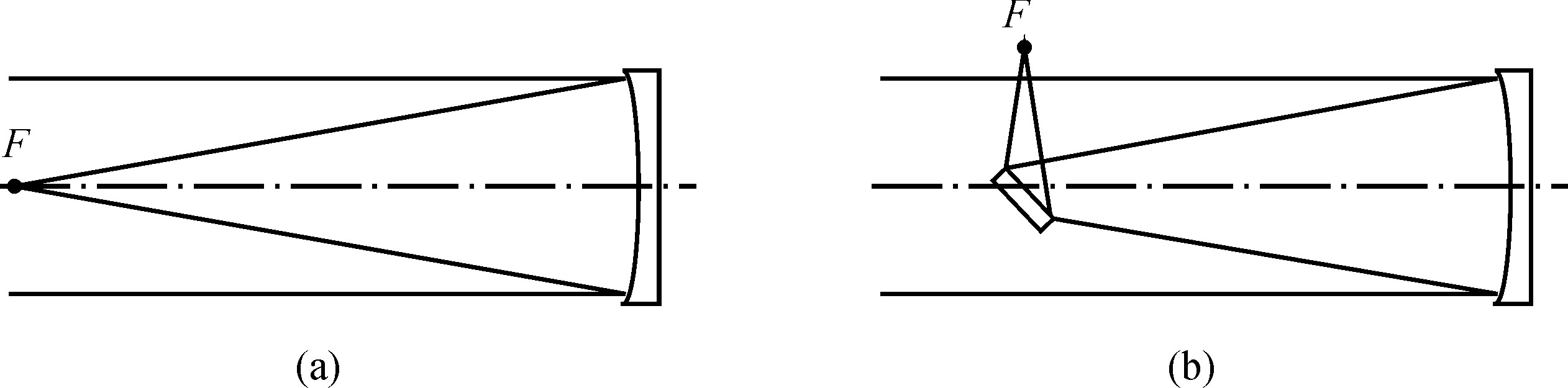
图1.22 (a)主焦点和(b)牛顿焦点的光学系统
牛顿(Newtonian)焦点与主焦点系统类似,只是增加了一块斜放的平面镜,使像点成像于镜筒的侧面(图1.22(b))。牛顿焦点的全部性质与主焦点相同,它仅比主焦系统多一块平面镜。牛顿焦点易于接近,观察方便,同时通过转动平面镜,可以取得不同的焦点位置,装置多种终端设备。牛顿焦点主要用于中、小口径的反射式望远镜中。在大口径光学望远镜中为了减轻镜筒顶部的质量,一般不使用牛顿焦点。
在主焦系统的焦点之前放置一块双曲面副镜,就构成了经典的卡塞格林(Cassegrain)系统。卡塞格林焦点通常在主镜的后方(见图1.23(a))。在卡塞格林焦点系统中,副镜的引入使焦点位置移出入射光路,因此可以安装较大的终端设备。位于主镜后面的焦点有易于接近,操作方便的优点,在天文观测中具有十分重要的地位和作用。卡塞格林焦点系统中,由于副镜的放大作用,焦比一般为 F /7到 F /15,特殊的双镜系统的焦比也可以超出这个范围。
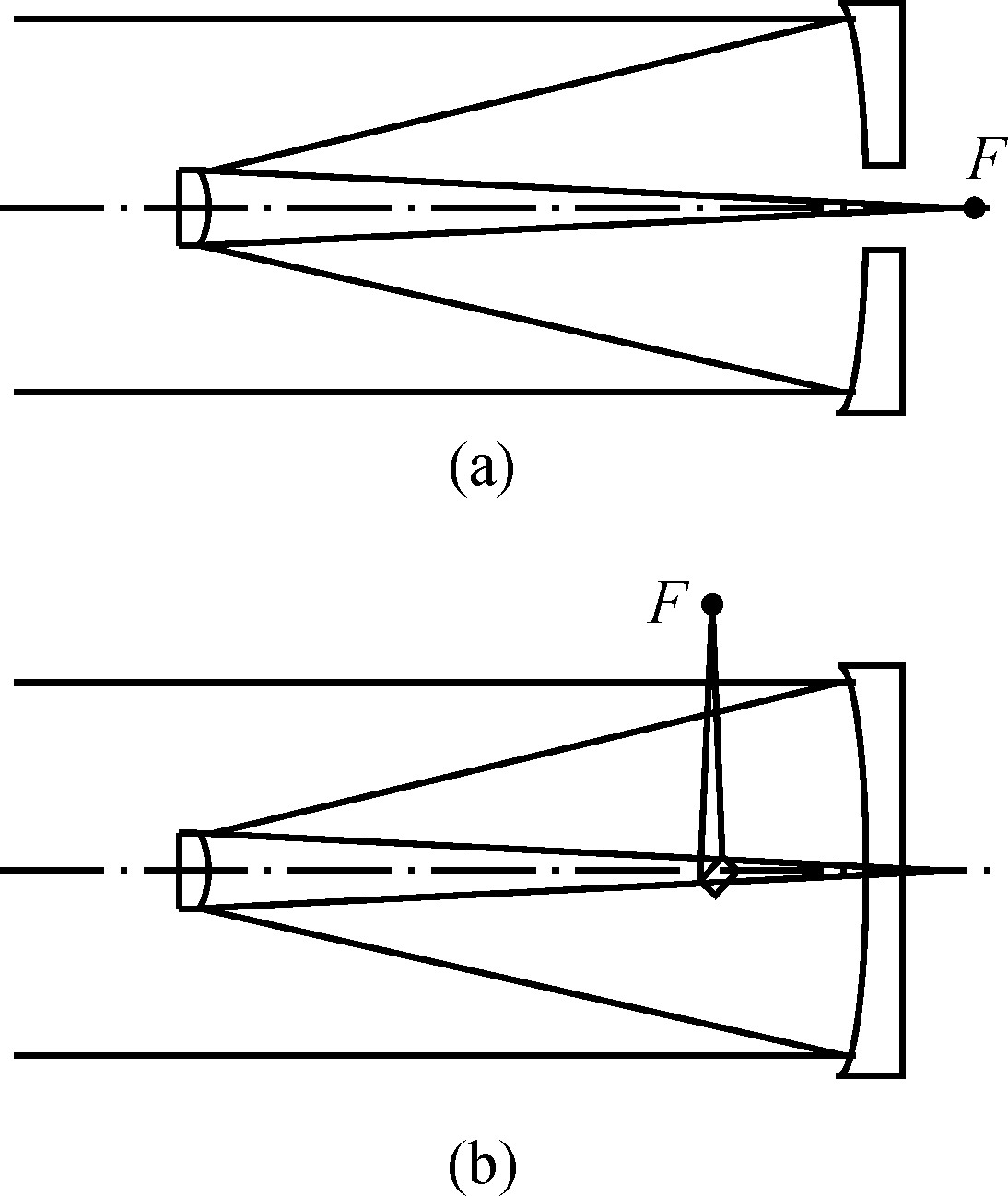
图1.23 (a)卡塞格林和(b)耐施密斯光学系统
经典卡塞格林望远镜的主镜是抛物面,副镜是双曲面。双曲面中的一个焦点与抛物面的焦点重合,望远镜成像在另一个焦点。和抛物面的主焦系统相似,像面仍然消球差,但是存在彗差,也有像散和场曲。由于卡塞格林系统比主焦系统焦比大,所以可用视场会大一些。主镜为抛物面,副镜为椭球面的系统叫做格里高利系统。从像差情况看,这种系统和卡塞格林系统基本相同。但是它具有真正的主焦点,在太阳望远镜中可以设置反射光阑将大量的热量反射出去。同时在副镜的下方有一个望远镜的出瞳,即主镜的像,因为出瞳上的各点和主镜面上的各点成共轭关系,所以可以在这个位置放置红外摆动镜或者放置改正主镜像差的小改正反射镜。
当光学系统满足阿贝正弦条件时,光线出射角的正弦和入射角的正弦成比例,系统将成理想的高斯像。如果在两镜系统中,同时满足等光程和阿贝正弦条件,这时系统会同时消除球差和彗差,这时系统的主镜和副镜均是双曲面形状。这种系统是由克莱琴(Chretien)提出、里奇(Ritch)研究成功的,被称为R-C望远镜系统。R-C系统的可用视场比一般的卡塞格林系统大很多,如果不使用场镜,像质为1角秒时,视场可达0.2度。不过在它的视场中仍存在像散和场曲,焦面是弯曲的。使用场镜后,视场可以达到0.4度。在R-C系统的焦点上存在球差,需要加入改正镜。一种配有改正镜优化后的R-C系统视场更大,可达1度以上,这种特殊的光学系统称为类R-C系统。类R-C系统离开改正镜后将不能进行CCD直接观察。双镜面系统还有其他的主、副面形状,如主镜或副镜是球面的特殊形式,这些系统存在各自的局限性。
在双镜面系统中添加一块倾斜45度的平面镜,可以将卡塞格林焦点移到光路以外,这就是耐施密斯(Nasmyth)焦点(见图1.23(b))。耐施密斯焦点在地平式望远镜中有广泛的应用。该焦点的受力条件不随镜筒的运动而变化,特别适宜安装大的精密仪器。
为了放置稳定的不随望远镜本体运动的大型终端设备,可以应用数面反射镜将光线沿望远镜轴线引出,抵达位于望远镜极轴或者地平轴延长线上的一个静止的焦点。这种焦点称为折轴焦点(图1.24)。折轴焦点焦比很大,焦点远离望远镜本体。折轴焦点仪器犹如一个实验室,输入的是天体的光辐射,输出的是星光的频谱或者其他的辐射特性。在折轴系统中反射镜通常为平面镜,但有时为了和卡塞格林焦点共用副镜也可以使用椭球面来改变光束的焦比。
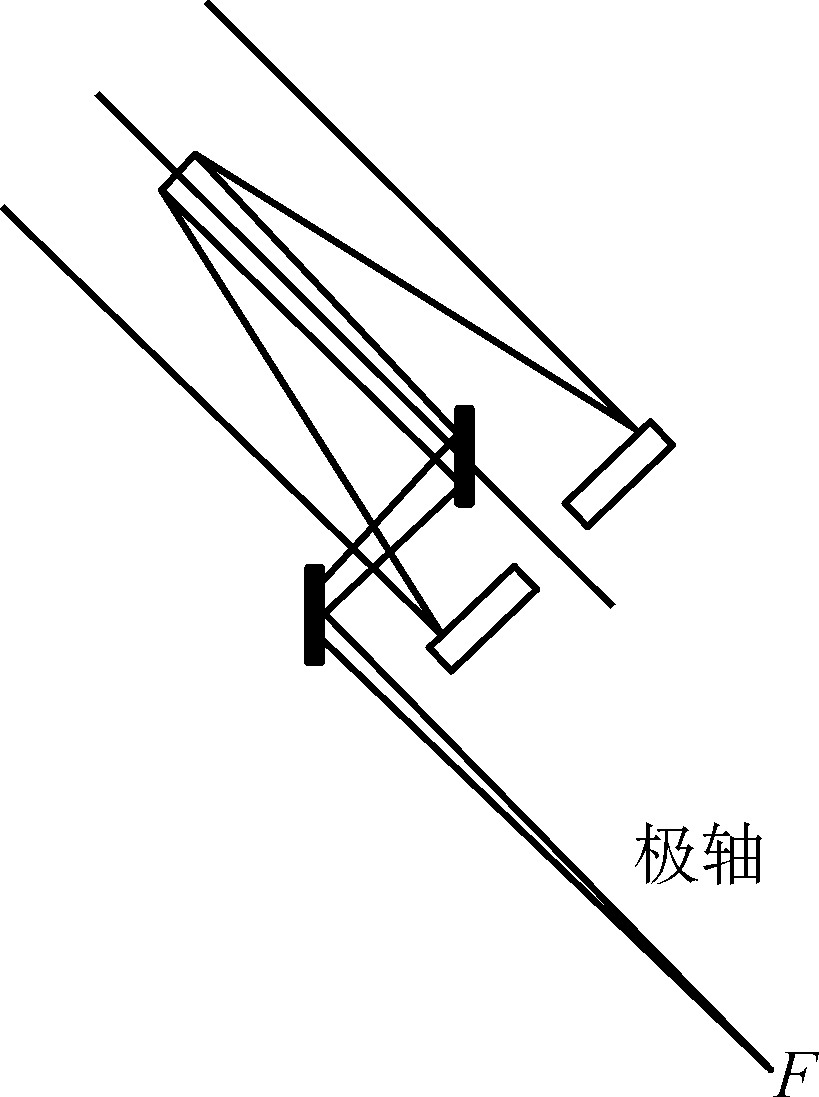
图1.24 望远镜的折轴焦点系统
上面介绍的望远镜焦点系统的一个共同特点就是望远镜可用视场很小,一般不适宜进行巡天工作。真正的突破发生在1931年,这一年施密特(Schmidt)发明了一种视场很大的折反射望远镜,即施密特望远镜(图1.25)。施密特望远镜的有效视场可以达到5×5度范围。施密特望远镜的主镜是球面,相对于球心,球面具有完美的对称性。所以施密特将望远镜入瞳设在主镜的球心,这样对不同方向的入射光除了光阑的投影略有差别外,成像条件完全相同,在光轴和光轴外的星像不存在差异。球面主镜具有球差和场曲,为了改正球差,引进了一块与平板玻璃差别很小的非球面改正透镜,即施密特改正板。施密特改正板的一面是平面,另一面的形状可以由几何光学直接导出。
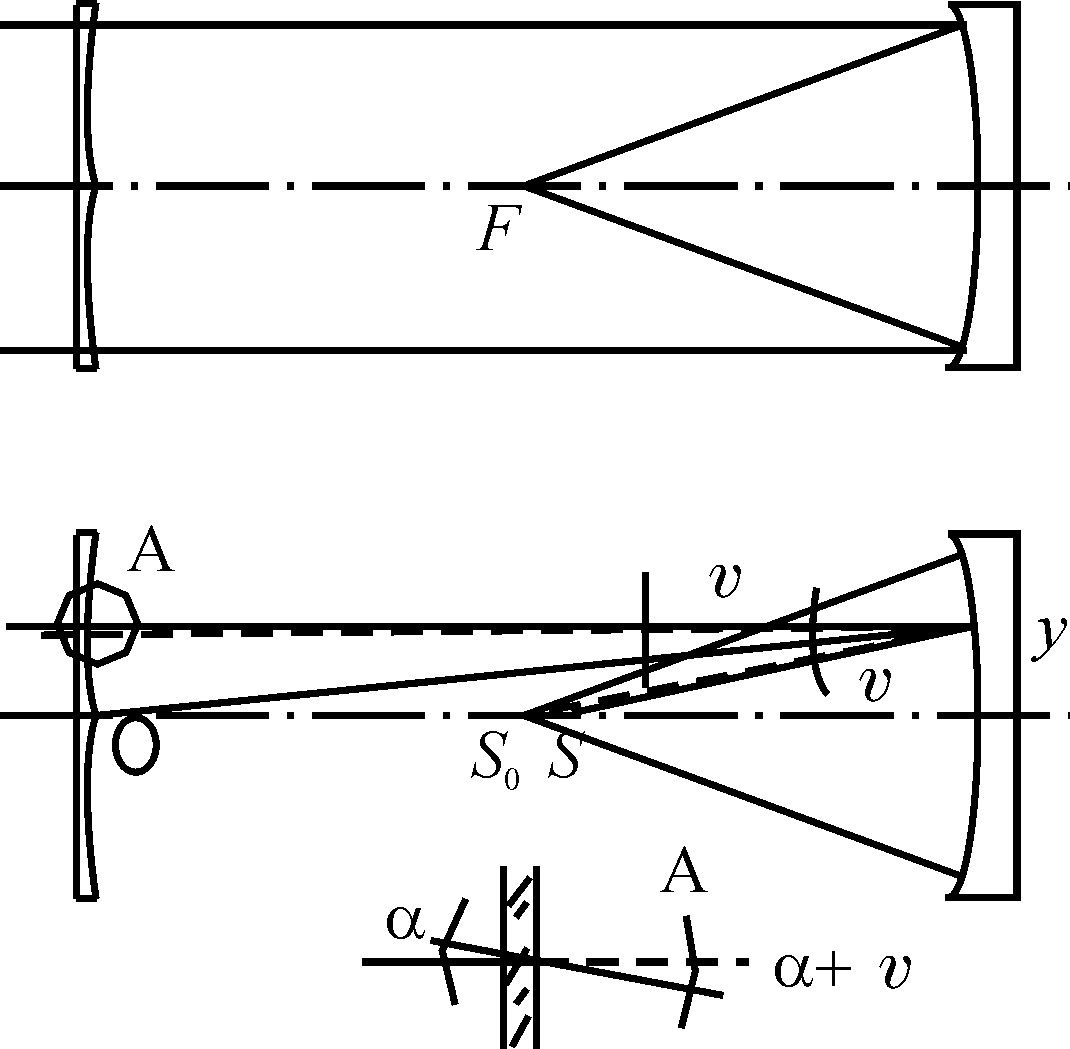
图1.25 施密特望远镜的折反射光学系统
设距离主光轴 y 0 处的平行光与主光轴会聚于 S 0 点,则任意高度 y 处的平行光与主光轴的交点 S 满足

式中 R 为球面主镜的半径。为了补偿这一球差,必须引入一个小的角度改正 θ

设 n 是改正板的玻璃折射率,则改正板在该处的斜率应该为

这块非消色差施密特改正板的曲面形状由下式表示,即

同理可以推导出消色差的改正板的形状,这时改正镜必须使用两片折射率不同的玻璃。使用非消色差改正板,为了使色差最小,可取
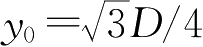 ,
D
是改正板直径。为了使望远镜有较大的无晕视场,施密特望远镜中球面主镜直径远远大于改正板直径。施密特望远镜的规格常常记为
a/b/c,a
表示改正板直径,
b
表示球面主镜直径,而
c
表示望远镜焦距。施密特望远镜视场大,光能损失小,改正板也比一般透镜薄,因此直径可以做到1.2米。
,
D
是改正板直径。为了使望远镜有较大的无晕视场,施密特望远镜中球面主镜直径远远大于改正板直径。施密特望远镜的规格常常记为
a/b/c,a
表示改正板直径,
b
表示球面主镜直径,而
c
表示望远镜焦距。施密特望远镜视场大,光能损失小,改正板也比一般透镜薄,因此直径可以做到1.2米。
施密特望远镜的焦面不是平面,如果想获得平面焦面,可以再加入一片场镜。配合物端棱镜和光纤摄谱仪,施密特望远镜可以进行十分有效的多目标光谱工作。施密特望远镜也可以用在成像要求较低的场合,在 γ 射线和宇宙线的探测中,有一种超广角的,像质要求低的荧光望远镜也是施密特望远镜的一种形式(第11.2.3节)。
在21世纪以前建造的大视场望远镜几乎全部是施密特望远镜。施密特望远镜有很多优点,它的缺点是:(a)改正镜形状特殊,较难加工和支承;(b)焦面是球面;(c)焦面位于光路之中,有挡光现象;(d)镜筒长,是焦距的两倍。由于改正镜的变形问题,世界上最大的施密特望远镜是1.4米口径。但是这台望远镜的性能并不很好,所以施密特望远镜的最大口径几乎是1.2米。2008年中国建成一台4米反射式施密特望远镜。在这台反射施密特望远镜中,必须实时控制改正反射面的面形,因而采用主动光学系统。
1940年马克苏托夫(Maksutov)也发明了一种大视场天文望远镜,即马克苏托夫望远镜。这种系统的改正透镜是新月形自消色差透镜。这个改正透镜厚度大,不适宜于大口径望远镜。现在马克苏托夫望远镜仅仅用于天文爱好者之中。
20世纪的后期,为了达到天文巡天的要求,光学专家对反射望远镜进行了深入研究。先后发展了大视场主焦改正镜,发展了类R-C光学系统,同时发展了一种三反射镜面大视场光学系统。各种改正镜的设计将在后面讨论,本节主要介绍三镜面大视场望远镜。
三镜面的早期系统中,主镜和副镜形成一个无焦的光束压缩器。在这个系统中,主镜是一面凹抛物面,副镜是一面共焦的凸抛物面,而第三镜是一个曲率中心位于副镜顶点的球面镜。这种系统和没有改正镜的施密特望远镜十分相似。保卢-贝克(Paul-Baker)改进后的系统中副镜曲率和第三镜相同(Wilson,2004),从而使系统消球差、彗差和像散。新系统存在场曲并具有大的中心遮挡,视场可以达到1平方度。维尔斯特罗普(Willstrop)将第三镜向主镜背后移动,使望远镜的焦面落在主镜平面上。为了实现更大的视场,对主镜形状也进行了优化,但保留了部分场曲。维尔斯特普的三镜面系统如图1.26(a)所示,其中主镜为准抛物面,副镜为准凸球面,第三镜是准凹球面。由于有较大余地进行系统优化,这种系统可以获得4×4度的有效视场。因为不存在透射元件,可能获得很大的集光面积。但是这种望远镜的镜筒很长。2010年美国空军耗资1.1亿美元制造一台3.5米三镜面长筒望远镜(DSST),视场达3.5度。梁明(2005)进一步改进了三镜系统,设计出一种短筒三镜面望远镜。在新设计中,第三镜前移到主镜平面,主镜和第三镜连成一体,形成一个单一连续的镜面。而望远镜的焦面则位于副镜面的附近(图1.26(b))。这种设计结构紧凑,镜筒长度减少了一半,已经应用于8.4米大口径巡天望远镜(Large Synoptic Survey Telescope,LSST)中,其角视场为3.1度,它是世界上具有最大集光率(etendue)的光学仪器,其集光量为319m 2 deg 2 。
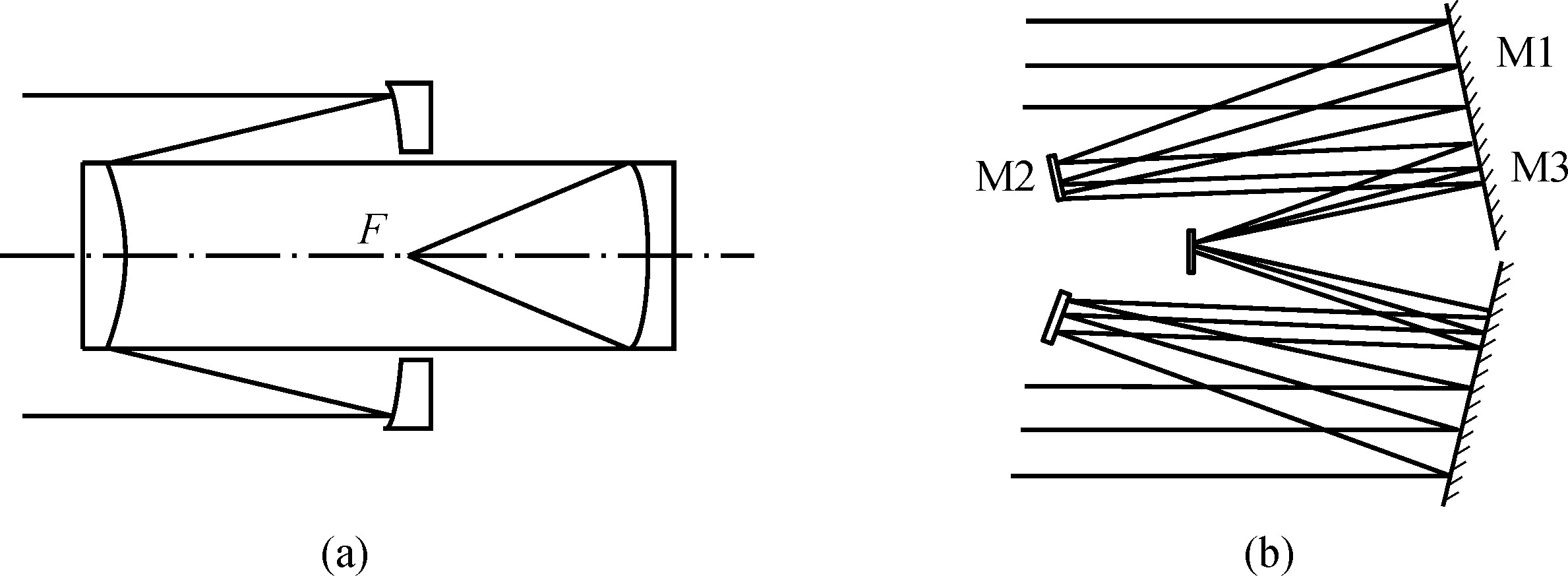
图1.26 维尔斯特罗普的三反射镜系统(a)和新的短筒三镜系统(b)
随着望远镜口径的增大,望远镜的镜筒会变得很长。镜筒的质量,成本以及其变形均是长度的三次方,而惯性矩则是长度高次方的函数。因此,使用折叠式光学系统,缩短镜筒长度,就有很大优点。折叠式系统是在主光路中插入平面镜,从而使副镜和主镜处在几乎相同的位置上,导致镜筒长度减少一半。
图1.27是一台折叠式格里高利系统。这里主副镜形成一个连续表面。如果这个系统用于红外波段,那么该复合镜面可以利用铝材金刚石车削获得。这种十分紧凑的光学系统可以作为非常灵敏的红外导航传感器。
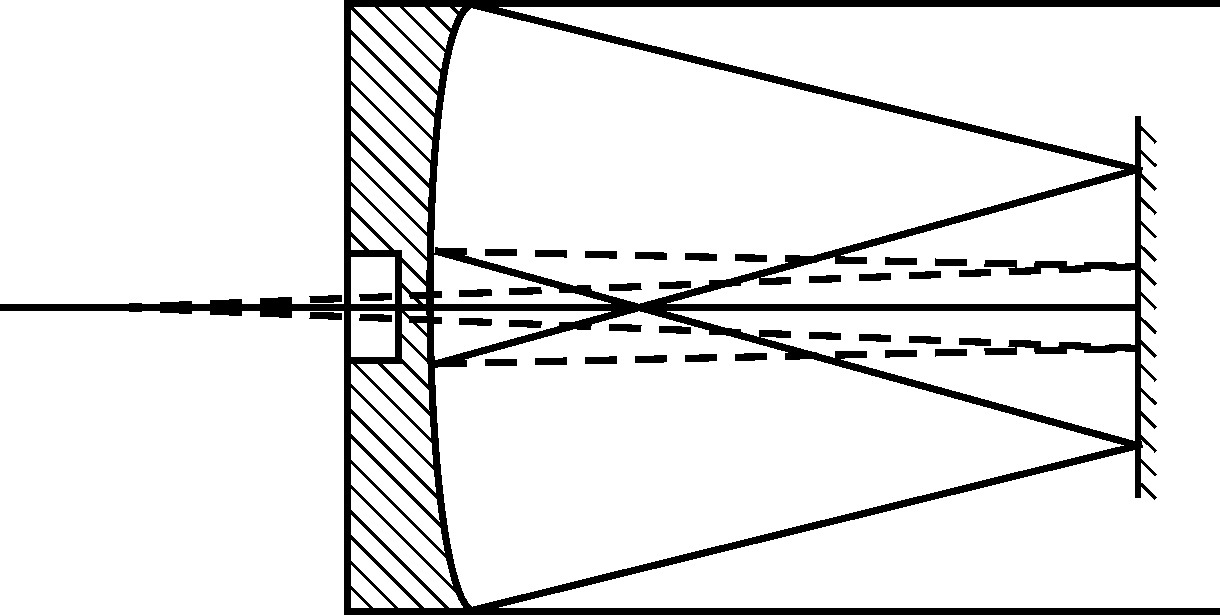
图1.27 折叠式的格里高利系统
欧洲南方天文台在口径100米超大天文望远镜的设计方案中也采用了折叠式主焦光学系统,如图1.28所示。在这一设计中,一面平面镜将主镜筒长度减少三分之一,使成像面处于主镜和平面镜之间。主镜的球差是通过四块反射镜面组成的改正镜组来校正的。不过这个雄心勃勃的方案已经为一个相对保守的40米级欧洲甚大望远镜所取代。
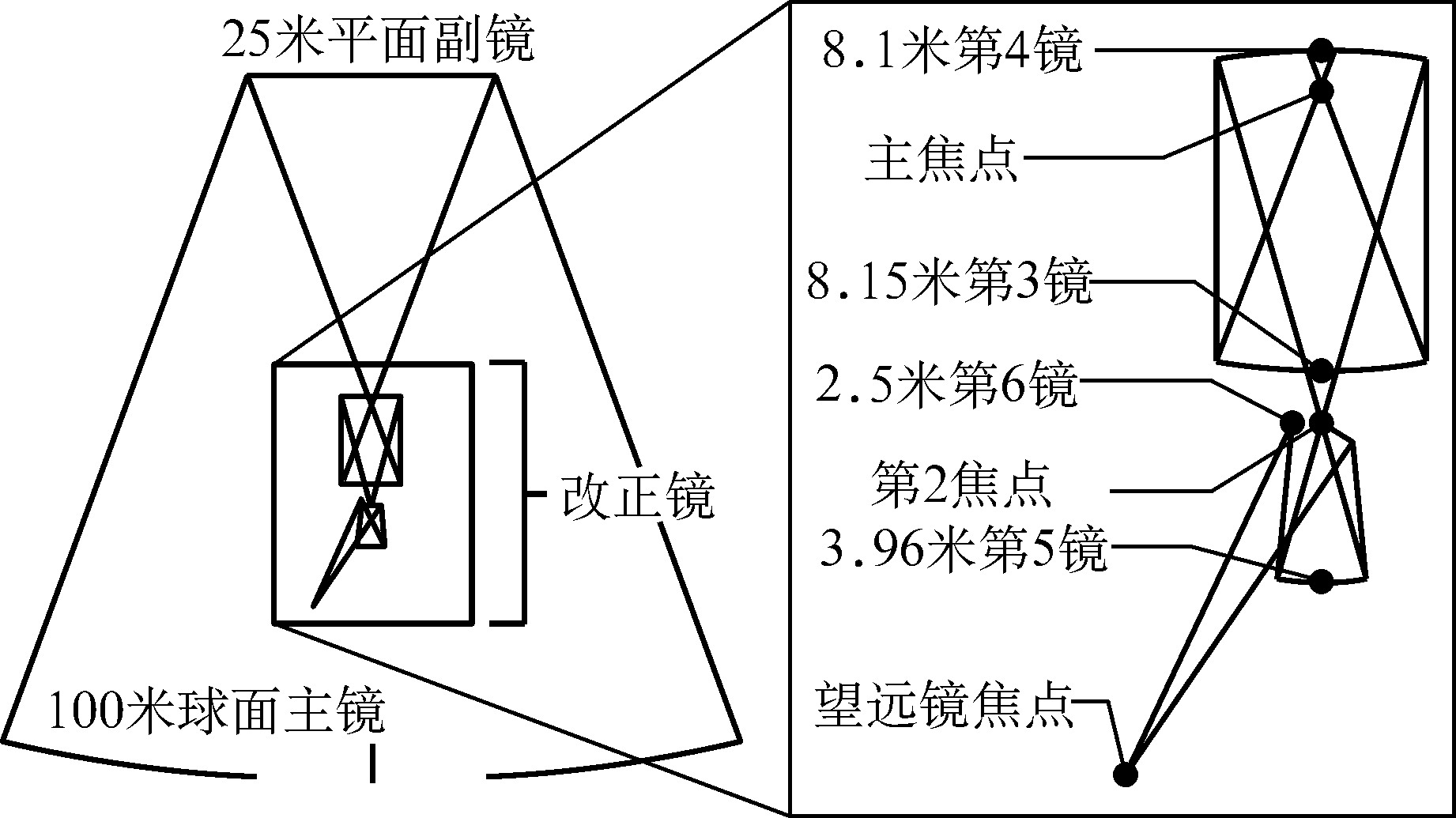
图1.28 欧洲南方天文台的100米超大望远镜的折叠式主焦系统(Dierickx,2004)
除了折叠式的光学系统以外,在X射线望远镜中还广泛使用掠射式光学系统(第10.2.2节),以提高望远镜的反射效率。
在空间望远镜中,有一种非常特殊的衍射式光学系统(diffractive optics)。已有的衍射式光学系统有菲涅尔透镜和光子筛(photon sieves)。菲涅尔透镜是由一个个具有半波长相位差的圆环形锯齿形透镜构成的,这些透镜带共同在焦点上成实像。由于这种透镜使用的材料要比普通透镜少得多,所以可以用来制造大口径望远镜。
在菲涅尔透镜中,包含一个个同心圆环,这些圆环被称为菲涅尔带。总的圆环数目为 N=D 2 /(8 λF ),式中 D 是直径, F 是焦距。菲涅尔透镜具有成本低,质量轻和制造要求低的特点。一般来说,菲涅尔透镜仅适用于一定的波长。对其他波长,它的焦距是不同的。菲涅尔透镜的主要缺陷是它的色差,不过通过成像数据的后处理,已经可以获得各个频段的成像信息(Lo and Arenberg,2006)。
光子筛,又称为菲涅尔板,是通过在一个不透明的平板或薄膜上形成一圈圈透光和不透光圆环带所形成的菲涅尔式成像系统。不过在光子筛中,这些透明圆环带是由一个个密集的透明小孔组成的,同样光子筛可以在焦点上成像。在光子筛中,小孔是不均匀分布的,它们互相不连通,所以光子筛的结构整体性好。在光子筛中,小孔直径随着它们距离中心点半径的增大而减小。小孔中心和光子筛中心点的距离由
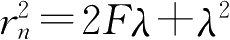 来决定,式中
F
是焦距,而每个环上孔的直径为
w=λF
/(2
r
n
)。现在已经制成的光子筛小孔总数达一千万个(Anderson and Tullson,2006)。
来决定,式中
F
是焦距,而每个环上孔的直径为
w=λF
/(2
r
n
)。现在已经制成的光子筛小孔总数达一千万个(Anderson and Tullson,2006)。
在本书中还介绍了其他一些非常特殊的光学系统,如在切伦科夫望远镜中利用球面子镜拼合成抛物面形状的Davis-Cotton光学系统(第10.3.6节);在X射线望远镜中利用球面镜、圆锥面镜或平面镜所形成的光学成像系统(第10.2.5节);以及在 γ 射线成像望远镜中所采用的特殊的编码口径(coded aperture)系统(第10.3.2节)。编码孔口径相当于针孔照相机,是一种非聚焦的光学系统,它的口径面由透明和不透明的单元组成,天体图像是由成像面上的复杂图像通过计算机计算而获得的,是计算照相法的一种形式。这种光学系统可以在背景光干扰强的高能区域使用。