凑十法

计算通常意味着一个接一个地进行几个独立的运算。计算时，先从哪一步开始或以哪一步结束，并没有什么区别。这就为我们将计算简化提供了可能性，比如凑十法。

我们看下面这个简单的加法：

7 + 2 + 5 + 13 + 8

你可以按照数字的前后顺序依次进行计算。不过，你也可以先仔细观察一下它们，很快你就会发现2和8、7和13简直是绝配，它们的和分别是10和20。如果在这个基础上再加上5，那么你就可以得到最终的结果35。看，这样就搞定啦。只要其中没有太多相加数，这都算一种既巧妙又好用的方法。因为如果相加数太多的话，你可能无法从整体上把控：哪些数是加过了的，哪些数还没加。

与10相关的计算对我们来说比较容易。在乘法运算中，我们同样可以巧妙地将数字重新排序。如果把这道题“46×35”中的数字重新排列，我们就可以用心算很快地算出答案。35的因数中有5，46的因数中有2，因此可以用5乘以2，结果等于10，所以我们可以这么写：

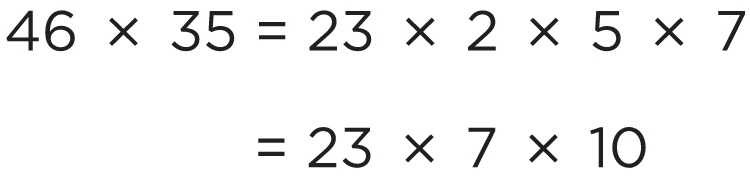
“23×7”我们可以用心算得出结果，它是140+21=161。因此，这道题的答案是：

46 × 35 = 1 610

另外，人们也许能一下子写出：

46 × 35 = 23 × 70

在这里，顺便提一下，少年时代的卡尔·弗里德里希·高斯（Carl Friedrich Gauss，1777—1855年）也通过巧妙地重排数字引起了人们的注意。当时，他的老师出了一道题：从1加到100，最后的总和是多少？

1 + 2 + 3 + 4 + 5 + … + 97 + 98 + 99 + 100

7岁的高斯将这些数分成了组，每组数相加的和均是101，即：

（1 + 100）+（2 + 99）+（3 + 98）+ … +（50 + 51）

他是用“凑101法”计算的。这位年轻的数学天才只需计算“50×101”即可，最终得到正确的答案5 050。 ItvkevBvW4eNGgWfEfNt7bieJyzeH2yLTGSotOiMm6PmZsyWbuM9ai1sUFHz28OJ