




在这一章节中,我将阐述通过地平圈的两极向黄道所画圆的角与弧的理论。这些圆通过地平圈的天顶,而地平圈上面的高度就取自这些圆。但是我已在前文里讨论过了太阳在正午的高度或黄道在中天的任何分度的高度,以及黄道与子午圈的交角。子午圈也属于通过地平圈天顶的圆之一。上升时的角度也已作过说明。从直角减去该角的余量,就是升起的黄道与通过地平圈天顶的象限所夹的角 (见图2.11) 。
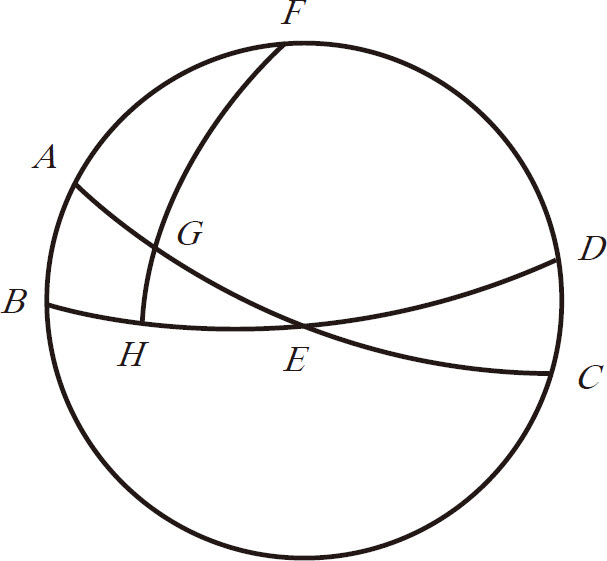
图2.11
再次画2.10所作的图,接下来就要讨论圆圈间的交点了
 。
。
在黄道上取正午和升起或正午和沉没间的任何点。
设:这一点为 G 。
通过
G
点从地平圈极点
F
画象限
FGH
。通过给定时辰,可知在子午圈与地平圈间黄道的整个
 。
。
已知:正午高度 AB 。
假定: AG 也已知。
那么:可求得 AF 。
子午圈∠ FAG 也可知。
根据前面关于球面三角形的论证, FG 可知,余量 GH 和∠ FGA 也可知。
以上关于与黄道有关的角度和交点的论述,是我在校核相关问题时从托勒密的著作中选择性摘引的。若有人想钻研该课题,可自行去寻找更为丰富的应用题材,以下我探讨的些许素材仅为举例:
在升起和正午之间,令其为η,其象限为ζηθ。通过给定的时辰,已知弧αηε,则可知αη和子午圈角为ζαη的αζ。故以球面三角形定理十一,可知弧ζη和角ζηα。以上即为我们所求。两倍εη和两倍ηθ所对弦之比,和两倍εα及两倍αβ弧所对弦之比皆与半径和角ηεθ的截距之比相等。所以可得固定点η的高度ηθ。另:在三角形ηθε中,已知边ηε、ηθ和角ε,而θ为直角。用这些量还可以求出角εηθ。