




接下来,我要说天穹被子午圈等分为两部分的情况。在24小时周期内,子午圈在黄道和赤道上各经过了一次。子午圈将黄道和赤道分割开,截出由春分点和秋分点(黄、赤道的交点)算起的圆弧。我们也可以说,由于与一个圆弧相截,子午圈被分割开了。因为都是大圆的缘故,它们构成了一个球面三角形。由于子午圈与赤道垂直,因此这个三角形为直角三角形。在该三角形内,子午圈的圆弧被称为黄道弧段的“赤纬”,而相应的赤道圆弧被称为“赤经”。
画一个凸三角形,一切就简单明了了 (见图2.1) 。

图2.1
令: ABCD 为同时通过赤道两极和黄道两极的圆(一般称它为“分至圈”),黄道的一半为 AEC ,赤道的一半为 BED , E 为春分点, A 为夏至点, C 为冬至点。
设:周日旋转的极点为
F
,并取黄道上的段长
 为30°,通过
G
点画出象限
FGH
。
为30°,通过
G
点画出象限
FGH
。
在△
EGH
中,已知边
 =30°,而∠
GEH
也已知。
=30°,而∠
GEH
也已知。
当它为最小时,取360°=4直角的分度法,它等于23°28′。这正好与赤纬 AB 的极小值相符。
因此,∠ GHE =90°。
根据球面三角形定理四,△ EGH 的各角和边都可知。
由此证得,两倍
 所对弦(即球的直径)与两倍
所对弦(即球的直径)与两倍
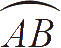 所对弦之比,等于两倍
所对弦之比,等于两倍
 和
和
 所对弦之比。
所对弦之比。
在它们的半弦之间也存在相似的关系。
设:两倍
 的半弦为100000
P
。
的半弦为100000
P
。
那么,两倍
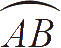 和
和
 的半弦各为39822
P
和50000
P
。
的半弦各为39822
P
和50000
P
。
假设:四个数成比例。
那么:首尾两数之积就等于中间两数之积。
因此,19911
P
(此处实际约为19909
P
)就是两倍
 的半弦。
的半弦。
∵在表里
 的值为11°29′,即与
的值为11°29′,即与
 段相应的赤纬。
段相应的赤纬。
∴在△
AFG
中,∠
FAG
为直角,而
 和
和
 两边作为两条象限的剩余部分,求得为78°31′和60°。
两边作为两条象限的剩余部分,求得为78°31′和60°。
那么:两倍
 、
、
 、
、
 和
和
 的半弦(或它们所对的弦)成比例。
的半弦(或它们所对的弦)成比例。
已知:两倍
FG
、
AG
、
FGH
的量,便可知
BH
为62°6′。这是从夏至点算起的赤经,或者从春分点算起为
 ,等于27°54′。
,等于27°54′。
同理,已知:
 为78°31′,
为78°31′,
 为66°32′及一个象限。
为66°32′及一个象限。
那么:∠
AGF
≈69°23
 。它的对顶角与此相等。另外,在其他情况下我们也将采用这一范例。
。它的对顶角与此相等。另外,在其他情况下我们也将采用这一范例。
我们不容忽视的事实是,子午圈与黄道正交于黄道和回归线相切的点。因为那时的子午圈通过黄道的两极。然而在两分点,子午圈与黄道的交角不会大于直角,而且随着黄赤交角偏离直角越多,这些交角就比直角越小,所以现在子午圈与黄道的交角为66°32′。另外,在黄道上量得的两段从两分点或两至点开始的相等弧长,与两个三角形的相等角或相等边同时出现 (见图2.2) 。

图2.2
设:画赤道弧
 及黄道弧
及黄道弧
 ,使两弧相交于
B
点,令其为一个分点。
,使两弧相交于
B
点,令其为一个分点。
取
 和
和
 为相等弧,通过周日旋转极点
K
和
H
,画两条象限
KFL
和
HGM
,得到△
FLB
和△
BMG
。
为相等弧,通过周日旋转极点
K
和
H
,画两条象限
KFL
和
HGM
,得到△
FLB
和△
BMG
。
令:边
 和
和
 相等,其对顶角在
B
点,且∠
FLB
和∠
GMB
都是直角。
相等,其对顶角在
B
点,且∠
FLB
和∠
GMB
都是直角。
∴根据球面三角形定理六,两个三角形的对应边与角皆相等,而且赤纬
 和
和
 相等,赤经
相等,赤经
 和
和
 相等,∠
F
等于∠
G
。
相等,∠
F
等于∠
G
。
如果相等弧是从一个至点量起的,可用相同方法进行阐述 (见图2.3) 。

图2.3
设:
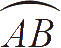 和
和
 为
B
点两侧的相等弧,回归线与黄道相切于
B
点。
为
B
点两侧的相等弧,回归线与黄道相切于
B
点。
从赤道的极点 D 画象限 DA 和 DC ,连接 DB ,得到两个相同的三角形△ ABD 和△ DBC 。
AB 和 BC 相等, BD 是共有边,而两个直角都经过 B 点。
根据球面三角形定理八,可证明△ ABD 和△ DBC 的相应边与角都相等。
显然,假定对黄道上一条象限作出这些角和弧的表,那么这个表将适用于整个圆周的其他象限。对此,我可以举例说明:第一栏为黄道度数,第二栏为与黄道度数相应的赤纬,第三栏为赤纬超过这些局部的赤纬的分数(在黄道倾角极大时出现),最大差值为24′。我对赤经与子午圈角度也按同样的方法编制 (如下表) 。



如果黄道倾角变化,那么与它相关的一切也应随之变化。赤经的变化很小,因为它小于一个单位时间的
 ,甚至在一小时内只有它的
,甚至在一小时内只有它的
 。关于与黄道分度一道升起的赤道分度如何表示,古代就出现了用以表述赤道分度的“时间”一词。这两个圆都有360个单位,但是为了加以区分,许多人习惯把黄道的单位称为“度”,把赤道的单位称为“时间”。我在后面也将采用这些名称。尽管这种变化小到可以忽略不计,但我仍会把它加进去。根据这些变化,便能对黄道的其他所有倾角得到相同的结果,但这需要假设对每一栏都能用相应的分数,且这个分数与黄道最大倾角和最小倾角之差成正比。例如,设倾角为23°34′,假定我想知道黄道上从一个分点量起的30°的赤纬的大小,那么可以在表一中找到11°29′,其差值为11′。当黄道倾角为极大时,就要加上这个差值。我在前面讲过,黄道倾角极大值可达23°52′。不过在当前的范例中可取值为23°34′,这比极小值大6′。而最大倾角超过最小倾角的24′的四分之一就正好是6′。按相同比值可得11′的部分约为3′。对11°29′加上3′,便得从至点量起黄道为30°时的赤纬为11°32′。子午圈角和赤经也可采用这种方法,但是后者应随时加上差值,而前者应减去差值,如此才能对任何与时间相关的数量得出更精准的结论。
。关于与黄道分度一道升起的赤道分度如何表示,古代就出现了用以表述赤道分度的“时间”一词。这两个圆都有360个单位,但是为了加以区分,许多人习惯把黄道的单位称为“度”,把赤道的单位称为“时间”。我在后面也将采用这些名称。尽管这种变化小到可以忽略不计,但我仍会把它加进去。根据这些变化,便能对黄道的其他所有倾角得到相同的结果,但这需要假设对每一栏都能用相应的分数,且这个分数与黄道最大倾角和最小倾角之差成正比。例如,设倾角为23°34′,假定我想知道黄道上从一个分点量起的30°的赤纬的大小,那么可以在表一中找到11°29′,其差值为11′。当黄道倾角为极大时,就要加上这个差值。我在前面讲过,黄道倾角极大值可达23°52′。不过在当前的范例中可取值为23°34′,这比极小值大6′。而最大倾角超过最小倾角的24′的四分之一就正好是6′。按相同比值可得11′的部分约为3′。对11°29′加上3′,便得从至点量起黄道为30°时的赤纬为11°32′。子午圈角和赤经也可采用这种方法,但是后者应随时加上差值,而前者应减去差值,如此才能对任何与时间相关的数量得出更精准的结论。