第1章
通过量的初值与终值的比率，我们可以证明以下命题

引理1

在任何有限的时间里，量和量的比值总是不断地接近相等，并在最后时刻趋于相等，差值小于给定的值，并最终实现相等。

如果否定这个观点，我们可以采用反证法来证明，假设它们最终不相等，并把 D 作为最终差值。这样，它们就不能以比给定差 D 更小的差值去趋于相等，但这与命题矛盾。

引理2

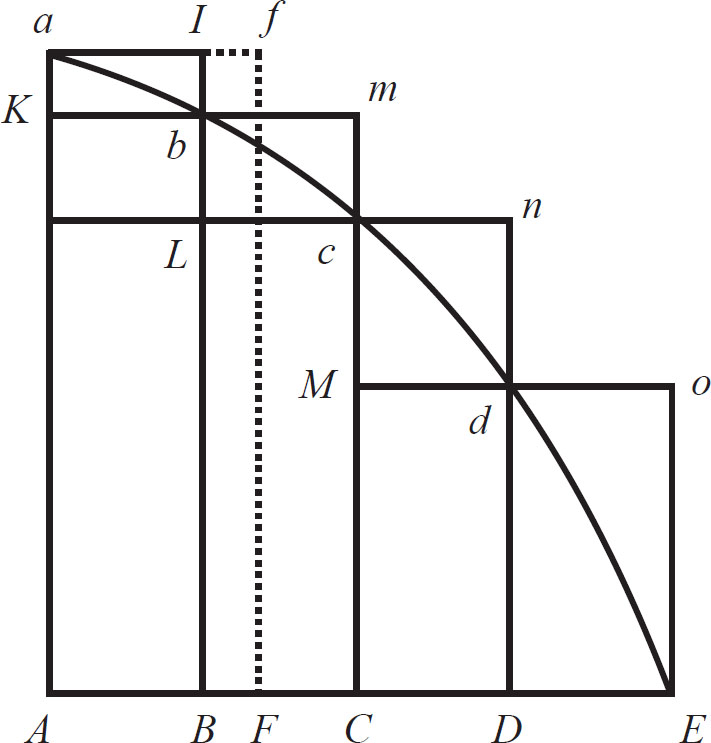
在任意图形 AacE 中，有直线 Aa 、 AE 和曲线 acE ，同时，有任意多个平行四边形 AKbB 、 BLcC 、 CMdD 等，底边 AB 、 BC 、 CD 等是相等的，侧边 Bb 、 Cc 、 Dd 等则与图形的边 Aa 平行。作平行四边形 aKbI 、 bLcm 、 cMdn 等，如果那些平行四边形的宽再减小，且平行四边形的数目近似无限，那么，曲线内切图形 AKbLcMdD 、外切图形 AaIbmcndoE 和曲线图形 AabcdE 的最终比值趋于等量之比。 （如图1-1）

由于内切图形与外切图形的差是平行四边形 KaIb 、 Lbmc 、 Mcnd 和 DdoE 之和，即 （底边相等） 以其中一个长方形的底 Kb ，以它们的高度和 Aa 为高的矩形，另一边之和是边 Aa 的平行四边形，也就是平行四边形 ABIa 。但由于这个平行四边形的宽 AB 是无限缩小的，因而平行四边形也就小于任何给定的空间。由此，根据引理1，内切图形和外切图形最终相等，而中间的曲线图形也相等。

证明完毕。

引理3

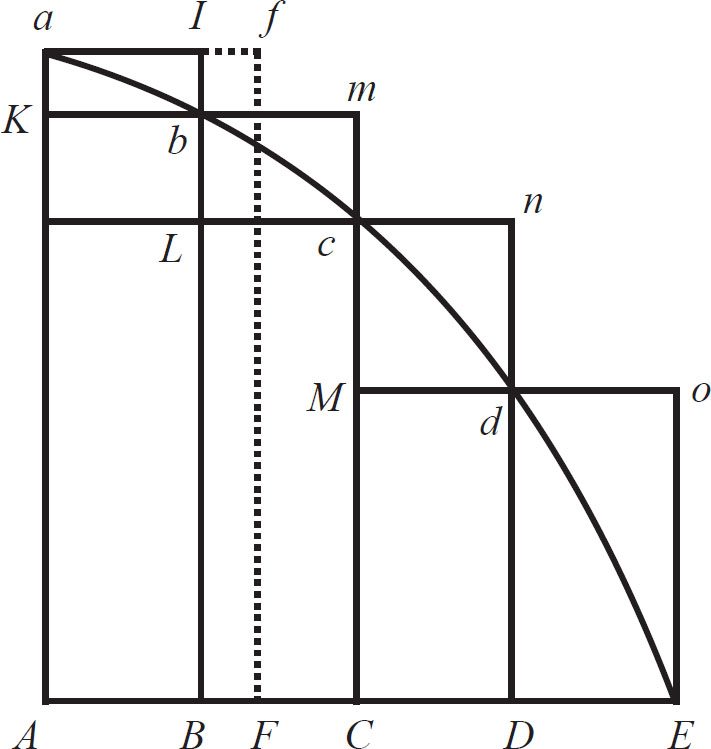
如果平行四边形的宽 AB 、 BC 、 CD 等不相等，且处于无限缩小时，最终比值也是等量之比。 （如图1-2）

假设 AF 为最大宽度，作一个平行四边形 FAaf ，那么，这个平行四边形将大于内切图形和外切图形的差，但由于此平行四边形的宽 AF 在无限减小，因此，它必将小于任何给定的平行四边形。

证明完毕。

推论1 那些逐渐减小的矩形其总和在所有方面都与曲线图形完全相符。

推论2 在逐渐减小的弧线 ab 、 bc 、 cd 等的弦构成的直线图形最终也与曲线图形完全相符。

推论3 切线弧长相等的外切直线图形，也与曲线图形完全相符。

推论4 这些外围为 acE 的最终图形并不是直线的，而是直线图形的曲线极限。

引理4

如果在图形 AacE 和 PprT 中，分别有一组内切平行四边形，若它们每组的数量相等，宽度趋于无穷小，并且，其中一图形内平行四边形的比值与对应的另一个图形内平行四边形的比值最终相等，那么，这两个图形 AacE 和 PprT 的比值也相等。 （如图1-3、图1-4）

因为其中一图形内的平行四边形与另一图形内的平行四边形是一一对应的，则这一图形中所有平行四边形的和与另一图形中所有平行四边形的和的比，就等于两个图形的比，因为，根据引理3，前一图形与总和之比，等于后一图形与总和之比。

证明完毕。

推论 由此可知，如果任意两个量被分为相同份数的若干部分，当它们的数目增多而自身在无限减小时，量相互间有一个给定的比值，且一一对应，整个量都以给定的比值相互对应。因为，在这个引理的图形中，如果将平行四边形的比值看成部分的比值，则这些部分的和一定等于平行四边形的和。假设平行四边形与部分的数目增大，而它们的量又无限减小，则这些和将是其中一图形中的平行四边形与相对应的另一图形中平行四边形的最终比值，即这些和是一个量里的任意部分与另一个量相关部分的最终比值。

引理5

在相似图形中，所有对应的边，无论是直线还是曲线，它们均成正比，且其图形面积之比等于其对应边之比的平方。

引理6

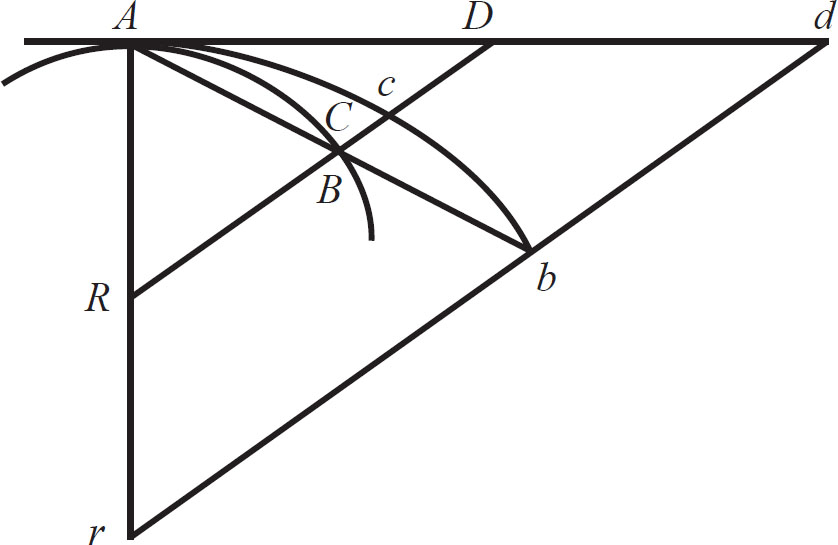
任意弧线 ACB 处在一个给定的位置，弧弦为 AB ，在连续曲线任意一点 A 上相切于直线 AD ，两边无限延长。如果点 A 与点 B 相互靠近且相遇，则由弦和切线构成的角 BAD 将会无限减小，直到最后完全消失。 （如图1-5）

因为，假如此角不消失，弧线 ACB 和切线 AD 将会构成一个直线角，而弧线在 A 点就不会延续其弯曲度，这与命题相互矛盾。

引理7

作同样的假设：弧线、弦和切线的比值最终相等。

当点 B 向点 A 靠近时，假设 AB 和 AD 总是分别趋向于两个遥远的点 b 和 d ，且平行于割线 BD 作一直线 bd ，使弧 Acb 总是相似于弧 ACB 。设点 A 与点 B 重合，根据前面的引理，角 dAb 会消失，所以直线 Ab 、 Ad （处于有限） 和中间弧线 Acb 将重合，且相等。因此，直线 AB 、 AD 和中间弧 ACB （与前者成正比例） 比值是等量之比 （如图1-5） 。

证明完毕。

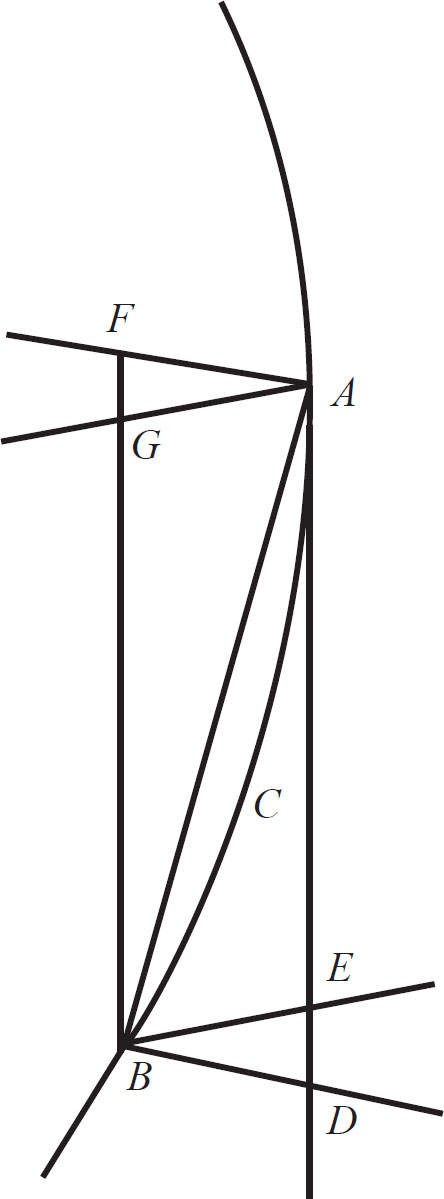
推论1 如果通过 B 点作 BF 平行于弧 BCA 的切线 AD ，且总是与通过点 A 的任意直线交于点 F ，那么直线 BF 与逐渐消失的弧 ACB 的比值最终成相等之比，因为在平行四边形 AFBD 中， BF 与 AD 的比值是等量之比。（如图1-6）

推论2 如果通过点 B 和点 A 作直线 BE 、 BD 、 AF 和 AG ，与切线 AD 及其平行线 BF 相交，则所有水平线 AD 、 AE 、 BF 和 BG 以及弦 AB 和弧 AB 的比值最终都是等量之比。

推论3 在所有关于最终比值的推论中，这些线段可以相互替换。

引理8

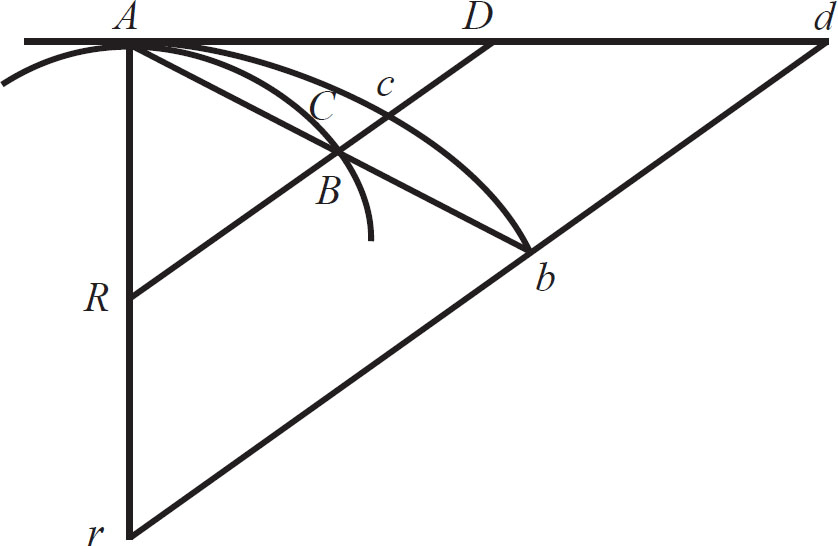
如果直线 AR 与 BR 、弧 ACB 、弦 AB 和切线 AD 共同构成三个三角形 RAB 、 RACB 和 RAD ，点 A 和点 B 相互靠近且重合，那么，这些逐渐消失的三角形最终是相似的，最终比值也是等量之比。 （如图1-7）

当点 B 向点 A 靠近时，假设 AB 、 AD 和 AR 总是分别趋向于遥远的点 b 、 d 和 r ，作出 rbd ，使其平行于 RD ，并使弧 Acb 总是相似于弧 ACB 。然后，再设点 A 和点 B 重合，则角 bAd 将会消失，而三角形 rAb 、 rAcb 和 rAd 则将重合，即相似且相等。那么，与它们总是相似和成比例的三角形 RAB 、 RACB 和 RAD ，最终也将相似且相等。

证明完毕。

推论 在所有关于最终比值的推论中，这些三角形可以相互替换。

引理9

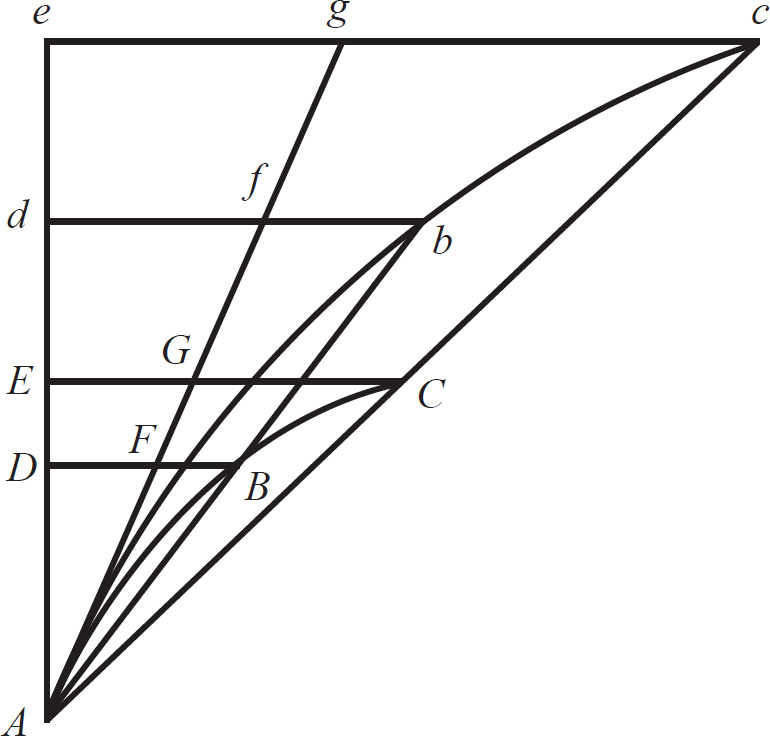
如果直线 AE 和曲线 ABC 均处于给定位置，且以给定的角在 A 点相交。直线 BD 、 CE 与直线 AE 也形成定角，并与曲线相交于点 B 和 C ，而点 B 和点 C 相互靠近且在 A 点重合，那么，三角形 ABD 、 ACE 的最终面积的比，将等于其对应边比值的平方。 （如图1-8）

当点 B 、 C 向 A 点靠近时，假设 AD 总是倾向于遥远的点 d 、 e ，而 Ad 、 Ae 将与 AD 、 AE 成正比。作线 db 、 ec 平行于直线 DB 和 EC ，并分别与 AB 、 AC 延长线相交于点 b 和 c 。使曲线 Abc 与曲线 ABC 相似，作直线 Ag 与两条曲线相切于点 A ，与直线 DB 、 EC 、 db 、 ec 相交于点 F 、 G 、 f 、 g 。然后，再假设 Ae 的长度保持不变，使点 B 和点 C 在 A 点重合，则角 cAg 将消失，曲线形面积 Abd 、 Ace 将与直线形面积 Afd 、 Age 相重合。因此，根据引理5，面积比将是对应边 Ad 、 Ae 比值的平方。不过， ABD 、 ACE 的面积总与这些面积成正比，而边 AD 、 AE 也与这些边成正比。由此可知， ABD 、 ACE 面积的最终比值为边 AD 、 AE 比值的平方。

证明完毕。

引理10

任一物体在有限力作用下所经过的路程，无论此有限力是可知不变的，还是连续增大或连续减小的，在运动的初始阶段与时间的平方成正比。

令直线 AD 、 AE 表示时间，直线 DB 、 EC 表示由时间产生的速度，那么，由速度所产生的距离就是由那些横线所构成的面积 ABD 、 ACE ，即根据引理9，运动的初始阶段距离与时间 AD 、 AE 的平方成正比。

证明完毕。

推论1 由此可以推出，物体在成比例的时间里通过相似图形的相似部分的误差，基本上与它们所产生的时间的平方成正比。这些误差是由应用在物体上任意相等的力产生的，并由物体到这些相似图形经过的距离求得，如果没有这些力的作用，物体会在那些成比例的时间内到达目的地。

推论2 由成比例的力（指的是类似地在相似图形的相似部分中运用在物体上的力）所产生的误差，与力和时间平方的乘积成正比。

推论3 用同样的道理可以解释物体在不同力的作用下经过的任意距离问题，在运动的初始阶段，这些距离与力和时间平方的乘积成正比。

推论4 力与运动初始阶段的距离成正比，与时间的平方成反比。

推论5 时间的平方与距离成正比，与力成反比。

附注

如果比较不同种类的未知的量，任何一个量都可以说是与另一个量成正比或者成反比的，即前者与后者以相同的比值增大或减小，或与后者的倒数成正比。如果说任意一个量与其他任意两个或者更多的量成正比或成反比，即前者与其他量比值的复合值，同其他量或其他量的倒数一起增大或减小。假如，设 A 与 B 、 C 成正比，与 D 成反比，则意味着 A 与 B × C × 以相同的比值增大或减小，即 A 与 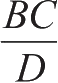相互之比为给定比值。

引理11

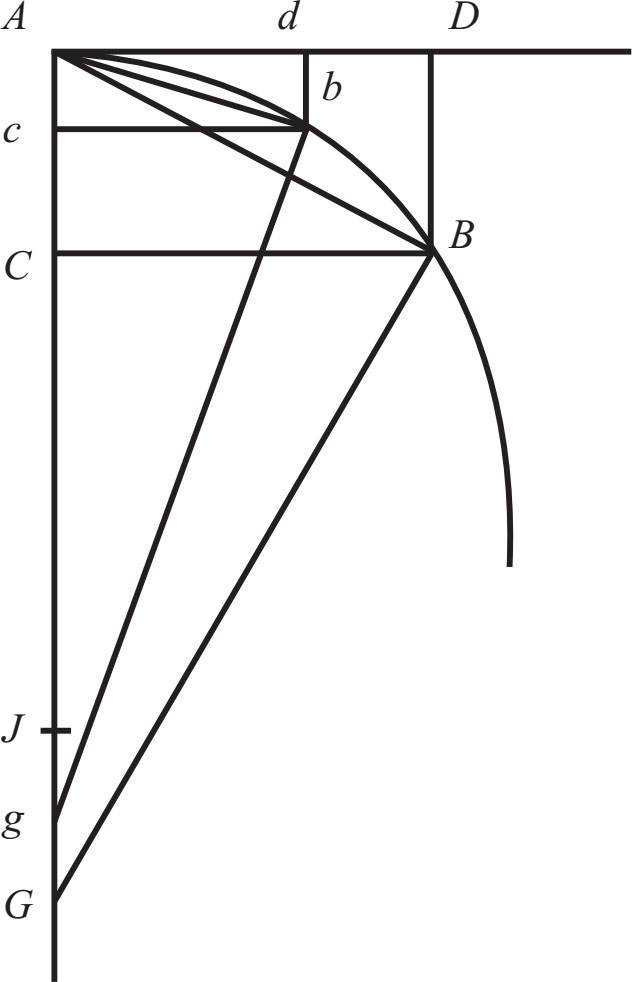
通过接触点的所有曲线有有限的曲率，而逐渐消失的接触间的弦最终与弧对应的弦的平方成正比。 （如图1-9）

情形1 AB 为一弧线， AD 为切线， BD 为接触角的弦，且垂直于切线 AD ， AB 为弧对应的弦。过 B 点作 BG 垂直于弦 AB ，过 A 点作垂线 AG 垂直于切线 AD ，二者相交于点 G ，再使点 D 、 B 、 G 趋近于 d 、 b 、 g 点，假设 J 点为直线 BG 、 AG 的最终交点，那么，点 D 、 B 与点 A 重合，显然，距离 GJ 就可能小于任何给定的长度。然而 （根据半圆 ABG ，半圆 abg 的性质） AB ² ＝ AG × BD ， Ab ² ＝ Ag × bd ，因此， AB ² 与 Ab ² 的比值是 AG 与 Ag 比值， Bd 与 bd 比值的复合。但因为 GJ 可能小于任何指定长度，故 AG 与 Ag 的比值与等量之比的差异也可小于任何给定的值， AB ² 与 Ab ² 的比值也和 BD 与 bd 的比值的差异可以小于任何给定的值。由此，根据引理1， AB ² 与 Ab ² 的最终比值和 BD 与 bd 的最终比值相等。

证明完毕。

情形2 使 BD 以任意角度向 AD 倾斜， BD 与 bd 的最终比值也与以前相等，因此， AB ² 与 Ab ² 的比值也相等。

证明完毕。

情形3 假设角 D 为任意角，而直线 BD 穿过一给定点，或者由其他任意条件决定。由相同规则决定的角 D 、 d 将总是趋于相等，并以小于任意给定差而相互靠近，据引理1它们最终相等，所以直线 BD 和 bd 相互间的比值仍与以前相同。

证明完毕。

推论1 当切线 AD 、 Ad 和弧 AB 、 Ab 以及它们的正弦 BC 、 bc 最终相等于弦 AB 、 Ab 时，它们的平方也将最终与弦 BD 和 bd 成正比。

推论2 它们的平方也最终与弧的正弦成正比，弦被二等分，并集中于一定点，因为这些正弦也与弦 BD 和 bd 成正比。

推论3 正弦与时间的平方成正比（所指时间为物体以给定速率沿弧线路径的所需时间）。

推论4 由边 AD 和 DB 及 Ad 和 db 的比值复合而得。直角三角形 ADB 和 Adb 之比最终与边 AD 的立方和 Ad 的立方成正比，并与边 DB 的 次方和 db 的 次方成正比，所以，三角形 ABC 和三角形 Abc 也最终与边 BC 的立方和 bc 的立方成正比。

推论5 因为 DB 和 db 最终平行，并与直线 AD 和 Ad 的平方成正比，所以，最终的曲线形 ADB 和 Adb 面积将（根据抛物线的性质）是直角三角形 ADB 和 Adb 面积的 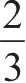，弓形 AB 和 Ab 部分是对应三角形的 。所以，这些曲线形面积和弓形将与切线 AD 和 Ad 、弦以及弧 AB 和 Ab 的立方成正比。

附注

然而，我们一直假设的切角不会无限大于或者无限小于由其圆周和切线构成的其他任意的切角，即处于 A 点的曲率既不是无限小，也不是无限大，而间隔 AJ 是一个有限的值。因为，我们可以使 DB 与 AD ³ 成正比，基于这种情况，在切线 AD 和曲线 AB 之间，没有任何一个圆能通过点 A ，所以切角将会无限小于这些圆周的切角。同理，如果将 DB 依次正比于 AD ⁴ 、 AD ⁵ 、 AD ⁶ 或 AD ⁷ 等，我们将会得到一系列趋近无限的切角，且后一项无限小于前面一项。如果 DB 依次正比于 AD ² 、 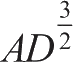、 、 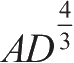、 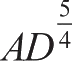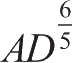或 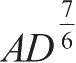等，我们将会得到其他一系列的切角，它们中的第一个与那些圆的切角为相同类型，第二个无限增大，且后一项无限大于前一个。但在这些切角的任意两个之间，又可以插入另一系列的中介切角，它们以两种方式趋于无限，每一个角都无限大于或者无限小于前一个。例如，在 AD ² 和 AD ³ 两项间插入了这一系列项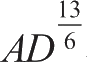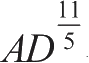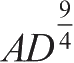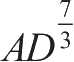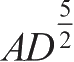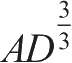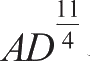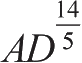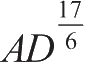： 、 、 、 、 、 、 、 、 等，同样，在这一系列角的任意两个之间，也可以插入一系列新的中介角，它们每一个都将随着无限的间隔而有所不同，可知这是无穷的。

曲线和其围成的表面所得到的规律，可以很好地运用于立体曲面及立体容积，这些引理可以避免古代几何学家那些繁复而难解的推导过程。在证明时，运用不可分方法将问题简化，但不可分的假设显得不够严谨，故这种方法被看做是缺乏几何化的方法。在后面的命题中，我会用开始与结束时的总和以及初量与逐渐消失的量的比值来证明，即用这些和与比值的极限，我将尽可能简洁地证明这些极限值。现在，不可分方法的已经得到了证明，运用起来就更加稳妥了。因此我在后面所说小部分构成的量，或者说用短曲线来替代直线，不是指不可分量，而是指逐渐消失的可分量；也不要理解为可知部分的总和及其比值，而是指的和与比值的极限，我在证明中所说的力是以前面所述引理为前提的。

也许有人会持反对意见，认为不存在逐渐消失的量的最终比值，因为在量消失之前，比值并不是最终的，而当量消失后，也就没有什么比值了。但是，根据相同的道理，我们也可以这样辩论：物体到达一固定点并停止运动，也就没有了最终速度，因为这个速度在物体到达该点前，其速度并不是最终速度，而当物体到达时，其速度已为零。答案很简单，因为最终速度表示的是物体移动的速度，既不是指它到达最后处所停止运动之前的速度，也不是指停止运动之后的速度，而是在它到达时的瞬时速度，即物体到达最后处所时的速度也让运动停止。用相同的方法，可以把逐渐消失的量的最终比值理解为既不是量消失前的比，也不是消失后的比，而是在消失那一瞬间的比。同理，可以把初量的最初比值看成是它们刚开始时的比，并且开始的和与最后的和是指它们开始运动及停止时的和（增大或减小时）。速度在运动最后之时将达到一个极限，但不会超过它，这就是最终速度。就是说，所有开始或结束的量以及比值都有一个相似的确定极限，要求出它们却是一个严格的几何学问题。然而，当我们在证明其他任何类似的几何问题时，我们只能用几何问题来解决。

也许有人会反对，说如果逐渐消失的量的最终比值是给定的，那么它们最终的量值也是给定的，即所有的量都将包括不可分量，而这又与欧几里得在《几何原本》第十篇中证明的不可通约量相矛盾。然而这个反对意见是以一个错误的命题为前提的。因为，当量消失时，它们的最终比值并不是真正的最终量的比值，而是聚到某一点并形成极限，并且无限减小量的比值以小于任意给定的值向极限靠近。但绝不超过，实质上也不会达到极限，这种情况在无限大的量上表现得更为明显。如果两个量的差是定值，而它们又无限增大，则这些量的最终比值也是定值，即等量之比，但给出此比的最后的或最大的量并没有被给定。因此，为了方便理解，我在后面所提到的最小的、逐渐消失的或最终的量，大家不要认为是确定了的量值，而应理解为无止境减小的量。 GhxKqDBYGZexcJvvyzzSejrleLiqavhlWM71xSi/g74nL6FlYzLfRNIfywCe+hzE