1.12　量杆和钟在运动时的行为

沿 K ′的 x ′轴放置一根米尺，令其起点与点 x ′＝0重合，终点与点 x ′＝1重合。问米尺相对于参考系 K 的长度是多少？我们只要求出在参考系 K 的某一特定时刻 t 、米尺的起点和终点相对于 K 的位置，就会知道这个长度。借助于洛伦兹变换第一方程，该两点在 t ＝0的时刻其值表示为

x （米尺始端）＝

x （米尺始端）＝

两点间的距离为

但米尺以速度 v 相对于 K 移动。因此，沿本身长度方向以速度 v 移动的刚性米尺的长度为 米，因而刚性米尺在运动时比静止时短，而且进行越快运动的刚性米尺就越短。当速度 v = c ，我们就有 ，对于比这更大的速度，平方根就变为虚值，由此的结论为：在相对论中，速度 c 的意义为极限速度，任何实在的物体既不能达到也不能超出它。

当然，作为极限速度的速度 c 的这个特性也可以从洛伦兹变换方程中看到，如果选取了大于 c 的 v 值，这些方程就没有意义。

反之，如果所思考的是静止在 x 轴上，相对于 K 的一根米尺，我们就应发现，当从 K ′去判断时，米尺的长度是 ，这与我们进行考察的基础，即相对性原理完全吻合。

从先验的观点来看，我们一定能够认识到变换方程中量杆和钟的物理行为，因为 z、y、x、t 的值正是借助量杆和钟所获得的测量结果。如果我们以伽利略变换为基础进行考虑，就不会得出量杆因运动而收缩的结果。

假设我们现在考虑放在 K ′的原点（ x ′＝0）上一个永久不变的秒钟。 t ′＝0和 t ′＝1对应于该钟的两滴答声。对于这两滴答声响，洛伦兹变换第一和第四方程式给出：

由 K 判断，该钟以速度 v 运动；由参考物体判断，该钟在两次滴答声之间所经过的时间不是1秒，而是比1秒钟长一些的 秒。由此可看出，该钟在静止时比运动时走得快一点。速度 c 在此的意义上也是一种不可达到的极限速度。

相关问题　伽利略变换

在同一时刻，同一物体的坐标从一个坐标系变换到另一个坐标系，叫做“坐标变换”。联系这两组坐标的方程，叫做“坐标变换方程”。

设两个惯性参考系 S 和 S ′，参考系 S ′，设时刻 t ＝ t ′＝0时，两坐标系的坐标原点 O 与 O ′重合，则某一时点 P 的坐标变换方程是：

这叫做“伽利略坐标变换方程”。

这个变换方程已经对时间、空间性质作了某些假定。这些假定主要有两条：

第一，假定了时间对于一切参考系都是相同的，即假定存在着与任何具体参考系的运动状态无关的同一的时间，表现为 t ＝ t ′。既然时间是不变的，那么，时间间隔在一切参考系中也都是相同的，即时间间隔与参考系的运动状态无关。时间是用钟测量的数值，这相当于假定存在不受运动状态影响的时钟。

第二，假定了在任一确定时刻，空间两点间的长度对于一切参考系都是相同的，也就是假定空间长度与任何具体参考系的运动状态无关。

经典力学时空观（绝对时空观） 牛顿说：“绝对的、真正的和数学的时间，就其本质而言，是永远均匀地流逝着，与任何外界事物无关。”“绝对空间，就其本质而言，是与任何外界事物无关的，它永远不动、永远不变。”

按照这种观点，时间和空间是彼此独立的，互不相关，并且不受物质和运动的影响。这种绝对时间可以形象地比拟为独立的不断流逝着的水；绝对空间可比拟为能容纳宇宙万物的一个无形的、永不动的容器。

伽利略变换是绝对时空观的数学表述。

伽利略速度变换法则：

加速度变换关系为：

在所有惯性系中，加速度是不变量。

相关问题　中国钟表技术史

12世纪，金人入侵中原，苏颂古钟被毁，中国传统制表技术辗转流传。蒙古人入主中土后，仅让占星术继续发展，以保国运，其余所有关系的学问，都一概漠然置之。

16世纪中叶，最早一批从欧洲传到中国的时钟，由耶稣会教士引入。他们以传扬基督信仰，建立天国为职志，借着传扬西方科学知识来达到宣教目的。1582年，第一个洋钟运入中国，并于同年12月27日献给两广总督陈瑞。

1601年，利玛窦神父到中国，向万历皇帝进贡一座有驱动坠的铁钟。它每小时发声四次；钟身置于木柜内，柜身刻有龙饰，以鹰嘴指示用汉字写成的时间刻字。利玛窦神父本人连同两位本地工匠造了一个铜钟，可以每隔两小时 （一更） 报时一次。

中国宫廷的造钟坊是清乾隆年间 （1736—1795年） 建立的，监督的沙林神父属下有差不多100名奴仆。

1810年左右，有几份报告提到当时在广东省售卖时钟的西方商人，说他们经营惨淡，原因是要面对来自本地产品的竞争——它们可以半价出售。

1824年，宝威兄弟从瑞士到广东经商，复兴钟表业。当时，宝威的手表是在纳沙泰尔的弗勒里耶生产。时至今日，这些地方仍然是制表中心。

1840年，宝威兄弟率先为自己的产品采用了中国的商标名称，叫做“宝哗”或“播威”，都是从“宝威”字音译而来的。直至20世纪初，这牌子仍然深受欢迎。

相关问题　中国测时工具的历史

杆影测时 古人很早就知道，直立的标杆影长不断地随太阳在天上的位置的不同而变化。看杆影比直接观测太阳要方便，但测时结果是不等时的。《史记·司马穰苴列传》中就有春秋时代“立表下漏”测时的记载。用杆影测时法测定中午的时刻精度很高，是中国古代用来校正漏壶计时的主要方法之一。

圭表 甲骨文中有关时间的字大多从日字，说明测时的依据是太阳。根据太阳的运动判断一天内的时间变迁，圭表是最早使用的仪器。一根竿子立在地上，可以根据影子的长短和方向判断季节和一天内的时刻，1967年在江苏仪征的一座东汉墓中出土了一件铜圭表，不用时可以折叠起来，像一把铜尺，使用时将圭从表的凹槽中立起，使用和携带都很方便。

日晷 在圭表的基础上发展起来的日晷到汉代已做得很精细，1897年和1932年先后在内蒙古、河南、山西出土了三块秦末汉初的晷仪，上有69条刻线，占盘面的2/3，其余部分没有刻线，当为黑夜见不到日影的部分。三块出土地点不同，而其结构和所刻字体都相同，这表明秦汉时圭表和晷仪已很流行。

漏刻 作为计量时间的仪器，漏壶是最早发明的。古籍载：“漏刻之作，盖肇于轩辕之日，宣乎夏商之代。”这可能是一种传说。较可靠的资料见于《周礼·夏官》，其中载有挈壶氏，由于古代的漏壶上面有一个提梁，故称挈壶。挈壶氏“掌挈壶，……以水火守之，分以日夜”。西汉以前的漏壶现在未见实物，传世最早的漏壶为西汉时制，1958年、1967年、1975年分别出土于陕西兴平、河北满城、内蒙古默特右旗，都是铜铸圆柱状，上有提梁，下有漏嘴，梁上方有小孔，是插刻箭的。

为了改进单壶漏水不均匀的缺点，东汉时代开始用二级漏壶，以便互相补偿，如张衡的漏水转浑天仪。

经过秦汉时代的发展和创造，圭表、仪象、日晷、漏刻等天文仪器得到很大发展，并已普遍使用，这些仪器构成了我国2000年间用于天文观测和时间工作的主要仪器系列。

相关问题　计时器具的种类

流量计时 最古老的守时工具无疑是泄水型漏壶。后来有以沙代水的沙漏，有以油灯耗油量多少来计时的灯钟，也有燃香的香篆钟 （香火在金属盒内沿篆字式的沟槽蜿蜒前进） 等等。中国现存最古的漏壶是西汉时代的。世界上现存最古的滴漏是公元前14世纪的埃及水钟。

机械钟 中国汉代天文学家张衡做的水运浑象，能显示恒星出没、中天等天象，与室外天象完全相符。这是世界上最早的水力推动的机械钟。

唐代天文仪器制造家梁令瓒所制的水运浑象，除能符合天象外，另立两个木人每刻自动击鼓，每辰自动击钟。这是张衡水运浑象的改良型机械钟。

在宋代，苏颂和韩公廉等共同创造水运仪象台。

元代有郭守敬制的大明殿灯漏。

明代詹希元造五轮沙漏。这些机械钟具有完整的齿轮系、凸轮和擒纵机构。

欧洲的机械钟开始于14世纪，此后盛行了约400年。

摆钟 1582年，伽利略发现了摆的等时性。

1656—1657年，荷兰惠更斯把摆引入机械钟，从而创立了摆钟。

1673年，惠更斯采用摆轮—油丝系统，造出一种便于携带的钟表。

1735年，英国哈里森首次制造出航海钟，解决了当时资本主义发展中亟待解决的航海定位问题。

1896年，法国吉尧姆研制低膨胀系数的合金钢，造出精度极高的天文摆钟。如果把钟装入真空的玻璃罩内，存放在地下室，保持恒温，即为天文摆钟，每天的误差不超过千分之几秒。 DXZ+b7BfheXE71zPNnEsqCnRb0APJoDn5uAmfM5NDSnxmCH7oN6b7qF0WrW6jxQj

1.13　速度相加法则　斐索实验

实际上，钟和量杆运动的速度与光速相比是相当小的，因此我们不会将前节的结果与真实的情况直接比较。但在另一方面，这些结果必然使你持有异议。因此，为了说服你们，我将从该理论中再推导出另一结论，从前面的论述中推导出这个结论是很容易的，而且它已被十分完善的实验所证实。

在本章 第六节 ，所取形式是经典力学假设的同向速度相加定理，它已经被我们推导出，当然，该定理也可以十分容易地由伽利略变换 （本章 第十一节 ） 推演出来。我们引入一个移动点，该点相对于坐标系 K ′按照下列方程运动来代替车厢里走动的人，即

x ′= wt ′

借助伽利略变换第一和第四方程，我们用 x 和 t 来表示 x ′和 t ′，得到其间的关系式：

x =（ v + w ） t

这个方程表示的是该点相对于坐标系 K 的运动定律 （人相对于路基） 。用符号 W 表示速度，我们得到与本章 第六节 一样的方程：

W = v + w （A）

但是我们也可以根据相对论来进行思考。在方程 x ′= wt ′中，我们必须明确用 x 和 t 来表示 x ′和 t ′，这是引用了洛伦兹变换的第一和第四方程。这样代替方程 W = v + w 的是方程

这个方程对应于以相对论为依据的另一个同向速度相加定理。但在这两个定理中，能更好地与经验相符合的是哪一个呢？对此，半世纪前，杰出的物理学家斐索做过的一个实验给我们以极其重要的启发。斐索实验曾由一些最优秀的实验物理学家重新做过，因此实验的结果是毋庸置疑的。这个实验涉及光以特定速度 w 在静止的液体中传播的问题。现在如果液体在管子 T 内以速度 v 流动，那么光在管内与箭头 （见下图） 所指方向的传播速度究竟有多快呢？

根据相对性原理，我们当然认定，不论液体相对于其他物体是否处于运动状态，光相对于它总是以同一速度 w 传播。因此，光相对于液体和液体相对于管子的速度皆为已知，我们需要求出光相对于管的速度。

于是我们又遇到了本章 第六节 的问题。管相当于铁路路基或坐标系 K ，液体相当于车厢或坐标系 K ′，光相当于沿车厢走动的乘客或本节引进的移动点。如果 w 用于表示光相对于管的速度，那么 w 就应依照方程（A）或方程（B）计算，这视伽利略变换或洛伦兹变换谁更符合实际而定。斐索实验（ 斐索发现了 w ＝ w ＋ v ，其中 是液体的折射率 ^[2] ，另一方面由于 与1比相当小，我们首先用 w ＝（ w ＋ v ） 代替方程（B），因而按照同一的近似程度可以用 w ＋ v 代替方程（B），而这与斐索的实验结果相合）的结论是支持由相对论推出的方程（B），而且其符合的程度也很精确，根据不久前塞曼 （19世纪，物理学家法拉第研究电磁场对光的影响，发现了磁场能改变偏振光的偏振方向。1896年，荷兰物理学家塞曼根据法拉第的想法，探测磁场对谱线的影响，发现钠双线在强磁场中的分裂。洛伦兹根据经典电子论解释了分裂为三条的正常塞曼效应。由于研究这个效应，塞曼和洛伦兹共同获得了1902年的诺贝尔物理学奖。他们这一重要研究成就，有力地支持了光的电磁理论，使我们对物质的光谱、原子和分子的结构有了更多的了解。） 所做的卓越的测量，说明了液体流速 v 对光的传播的影响确实可以用方程（B）来表示，并且误差在1%以内。

不过我们必须注意到，早在相对论之前，洛伦兹就提出了关于这个现象的纯属电动力学性质的一个理论，这个理论是引用物质的电磁结构的特别假说而得出。然而无论如何这并没有减弱这个实验作为相对论支持者的说服性，因为最初的理论是由麦克斯韦—洛伦兹电气力学建立起来的，它与相对论并无丝毫抵触。说得更恰当些，电气力学是相对论发展的根基，它们既相互独立，又能组成电动力学本身的各个假说的综合和概括。

电动力学是研究电磁现象的经典的动力学理论，它主要研究电磁场的基本属性、运动规律以及电磁场和带电物质的相互作用。同所有的认识过程一样，人类对电磁运动形态的认识，也是由特殊到一般、由现象到本质逐步深入的。人们对电磁现象的认识范围，是从静电、静磁和似稳电流等特殊方面逐步扩大，直到一般的运动变化的过程。

相关问题　位移—时间图像

简称“位移图像”，它是用图像来表示物体位移和时间的关系。匀速直线运动的位移 s 是时间 t 的正比例函数， s ＝ v t 。在物体的直线运动中以横轴表示物体运动的时间 t ，纵轴表示物体运动的位移 s 。

s － t 图像的用途有：已知 s 求相应的时间 t ；已知 t 求相应的位移 s ；还可从直线的斜率的数值得出速度的大小。在同一坐标平面上，斜率越大，则直线越陡，表示速度越大，故可由图线求速度。

速度—时间图像

简称“速度图像”。它是用图像来表示匀速直线运动的速度和时间的关系。当物体做直线运动时，在平面直角坐标系中，用横轴表示时间，纵轴表示物体运动的速度。借助速度—时间图像可以找到运动物体在任何时刻的即时速度。它的用途较多。例如，已知时刻 t 可求相应的速度 v t ；已知即时速度 v t ，可求相应的时刻 t ；图像斜率的大小表示加速度的大小，斜率的正负表示加速度的方向，故可由图线求加速度；用速度图像求质点在任何时间内的位移，位移的数值相当于速度图像曲线下的“面积”的数值，这个“面积”的单位是米 （米／秒×秒） ，而不是平方米；可在同一坐标上比较几个物体的运动状况；并可判断某一运动过程中的几个阶段的运动性质与状况。

直线运动

质点在一条确定直线上的运动，称为“直线运动”。质点的位置，以离原点的距离、或坐标 x 表示。它是研究复杂运动的基础。按其受力的不同可分：匀速直线运动、匀变速直线运动 （包括匀加速或匀减速直线运动，以及自由落体，竖直上抛、下抛运动） 、变速直线运动。

匀速直线运动

物体沿一直线运动且在任何相等的时间里位移都相等，或者说速度的大小和方向都不改变的运动，谓之“匀速直线运动”。它的特征是：速度是一个恒量，即任一时刻速度（ v ）都相同。它的数学表达式是 ，或 s = v t 。式中 s 是位移， t 是发生这段位移所经过的时间。产生匀速直线运动的条件是：当运动物体所受外力的合力等于零时，物体做匀速直线运动。所以，真正的匀速直线运动实际上是很难出现的。为简化问题，不妨碍结果的准确性，而把近似的匀速直线运动当作真正的匀速直线运动来处理。

变速运动

亦称“非匀速运动”。物体的速度随时间而变化，可能是快慢程度，也可能是运动方向发生变化，还可能是快慢和方向同时都发生改变。它是最常见的一种机械运动。按其运动的轨迹来分有直线运动和曲线运动两种。

变速直线运动

在相等的时间里，位移并不都是相等的直线运动。它是物体运动最常见的形式之一。由于物体运动的快慢经常改变，所以常用平均速度和即时速度这两个物理量来描述物体运动的快慢程度。

匀变速直线运动

加速度的大小和方向保持不变的直线运动。匀变速直线运动的基本特点是：在任何相等的时间内其速度的增量相等。质点在做匀变速直线运动时，其速度图线 v － t 图是一条倾斜的直线，而直线的斜率就等于其加速度的大小，即

式中 v 0 、 v t 依次为做匀变速直线运动的初速度和末速度。它的运动规律可通过几个公式反映出来：速度（ v t ）与时间（ t ）的关系是 v t ＝ v 0 ＋ at ；位移与时间（ t ）的关系是 ；速度（ v t ）与位移（ s ）的关系是 。当加速度是一个正恒量时，物体的运动叫匀加速直线运动；当加速度是一个负恒量时，物体的运动叫匀减速直线运动。当物体受到一个与 v 0 同方向或反方向的恒力的作用时，或者物体受到几个力的作用，这些力的合力的方向与 v 0 的方向相同或相反，合力的大小保持不变时，物体就做匀变速直线运动。

匀变速直线运动的规律可以通过下列公式反映出来，即

速度公式 v t ＝ v 0 ＋ at

位移公式

速度路程公式

公式中共有 v 0 、 v t 、 s 、 a 、 t 五个物理量，除 t 之外，其余四个都是矢量，因此必须注意它们的方向。由于物体是做直线运动，故只需用正、负号即可表示它们的方向。通常规定初速度 v 0 的方向为正方向。当加速度 a 与 v 0 反向时， a 为负，物体做减速运动。速度位移公式是由速度公式和位移公式联立消去 t 以后得到的。可见，上述三个公式中只有两个独立，在 v 0 、 v t 、 s 、 a 、 t 这五个量中必须给出三个，才能通过公式找出另外两个来。

运动叠加原理

亦称“运动的独立性原理”。是物体运动的一个重要特性，是物理学中的普遍原理之一。一个物体同时参与几种运动，各分运动都可看作是独立进行，互不影响的。而物体的合运动是由物体同时参与的几个互相独立的分运动叠加的结果。例如，初速不为零的匀变速直线运动是由物体同时参与的速度为 v 0 的匀速直线运动，和初速为零的匀变速直线运动叠加的结果。又如，平抛物体运动，由竖直方向的自由落体运动和水平方向的匀速直线运动叠加而成，而这两个运动是彼此独立的。

运动的合成

已知物体的几个分运动求其合运动谓之“运动的合成”。由于一个物体常常在同时做几种运动，其中任何一种运动，不影响其他运动。为研究方便起见，将这个物体的整体运动看作是由几个分运动所组成的合运动。运动的合成是指位移的合成、速度的合成或加速度的合成，运动的合成遵从矢量的合成。当物体同时做两个匀速直线运动时，则其合运动也是匀速直线运动。当物体同时一个做匀速直线运动，一个做初速度为零的匀加速直线运动时，若两者在一直线上，则其合运动也是直线运动；若两者不在一直线上，则其合运动是曲线运动。

斐索实验

1851年，斐索观察循环水流中光速的著名实验支持了斯涅尔在光“以太”学说基础上对运动介质中光速给出的解释。斯涅尔公式为

反射光

折射光

前两式表示反射波的两个分量和入射波两个对应分量之比，后两式表示折射波和入射波两个对应分量之比，振动方向的变化则由正负号来决定。

在狭义相对论创立之前，斐索实验曾是光“以太”学说的判定性实验之一，并被用来说明光介质能够为运动物体所部分拖动。 +mwSd6IMzy2kMBmlgSszQ8nWUIKr/HIidmPjFBBxS+tmkopUgiLFf/J7eTOvysd7

1.14　对相对论启发作用的评估

在前面各节中，我们的思路可概述如下：经验在一方面使我们确信，相对性原理是正确的；在另一方面，光在真空中的传播速度被认为等于恒量 c 。把这两条结合起来，便得出有关构成自然界过程诸事件的直角坐标 x、y、z 和时间 t 在量值上的变换定律，这一点与经典力学不同，它不是伽利略变换，而是洛伦兹变换。

光的传播定律是我们目前的知识可以接受的一个定律，它在我们的思考过程中起了重要的作用。可一旦有了洛伦兹变换，我们就能结合洛伦兹变换和相对性原理，将这个理论概括如下：

每一个普遍的自然界定律必须由以下正确严密的定理建立，若代替最初的坐标系 K 的空间—时间变量 x、y、z、t 是我们新引用的坐标系 K ′的空间—时间变量 x ′、 y ′、 z ′、 t ′，那么经过变换以后该定律仍与原来的形式完全相同。这里，带着重符号的量和不带着重符号的量之间的关系就由洛伦兹变换公式来决定，或简而言之，普遍的自然界定律对于洛伦兹变换是变异的。

这是相对论对自然界定律所要求的一个明确的数学条件。有鉴于此，在帮助探索普遍的自然界定律中，相对论具有极其宝贵的启发作用。如果发现一个具有普遍性的自然界定律并不满足这个条件的话，就证明相对论的两个基本假定之中至少有一个是不正确的。迄今为止，相对论究竟已经确立了哪些普遍性结果呢？现在让我们来看一看。

相关问题　狭义相对论的问题

爱因斯坦坚信世界的内在和谐，追求理论的逻辑统一，不能容许惯性系与非惯性系之间这种内在不对称情况的存在。解决这个难题的办法，就是把狭义相对论原理扩大到非惯性系统。

狭义相对论的另一个严重困难来自引力，因为它与牛顿的引力公式和引力势方程不相容。

牛顿的引力公式即是万有引力定律公式。

万有引力：宇宙中任何有质量的物体之间的相互作用。

万有引力定律：宇宙间的一切物体都是相互吸引的。两个物体间的引力大小，跟它们之间质量的乘积成正比，跟它们的距离的平方成反比。

万有引力公式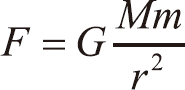： 式中， G ＝6.67×10 -11 N·m 2 /kg 2 ，为万有引力恒量； M 、 m 是两物体的质量； r 为两物体的中心距离。

狭义相对论提出后，许多人曾致力于检验各种物理定律在洛伦兹变换中的协变性，他们都获得了成功。但是包括爱因斯坦本人在内，都发现一个问题：当把牛顿引力理论纳入到相对论理论之中时，却遇到了明显的矛盾。起初，爱因斯坦试图寻找一个描述引力场变化的结构定律。他在狭义相对论的框架内处理引力定律，以期推出引力的场定律。可是，研究的结果却出乎意料：落体的加速度与它的内能有关。这让爱因斯坦认识到，在狭义相对论的框架里，不可能有令人满意的引力理论。

寻找第二个爱因斯坦

10道有趣的问题

一封来自美国普林斯顿大学的电子邮件中，10道没有标准答案的物理研究课题将激活人们的无限想象。

你喜欢科学或者不喜欢，这都不要紧，但希望你总还有点热情和好奇心。

“好奇心”就是下一个爱因斯坦诞生的起点。

1.让我有一个彩色的影子。 每个人都有一个独一无二的影子，在印象中影子似乎只有黑色一种。世界上会有彩色影子吗？是否能依照自己的样子为自己设计出一个彩色的影子呢？

2.自制自行车里程计。 汽车都有里程表，我们能不能给自行车也装个里程表呢？如何用机械或电子的方法将自行车轮的每一次转动自动记录下来，并将其转换成公里数？

3.自制一个能测液体密度的杆秤。 我们平时遇到的一些液态商品的质量可能同其密度有关。给你一根杆秤，外加一些小配件，如何才能方便地测出液体的质量呢？

4.设计一个不受太阳位置变化影响的太阳灶。 太阳能是一种绿色可再生能源，但用太阳灶加热物品有个麻烦，那就是相对太阳灶来说太阳的角度在不停地变化。能不能设计一种太阳灶，让太阳不论在什么位置都有一个同样的焦点呢？

5.设计一套家庭节水方案。 我国的水资源非常紧缺，节约用水是我们每个人的责任。作为一个家庭，如何用水更合理？

6.设计社区生活垃圾分捡和回收方案。 日常生活中会产生大量生活垃圾，有些有毒物会污染环境，能否利用各种垃圾不同的物理性质，设计一种分离装置方便地把垃圾分捡开来，将有用的部分回收，有毒的东西妥善处理呢？

7.设计一套以太阳能为主要能源的环保型家庭能源方案。 作为一个现代人，又想环保又不想过原始人的生活。那么，一个现代化的家庭能否只用太阳能就可以生活呢？

8.设计一个自动关门装置。 不用电机，不用弹簧，如何把开门的能量保存起一部分用来关门呢？

9.利用发光二极管设计一个不用电池的手电筒。 发光二极管可是个好东西，发光效率高而且寿命还很长。让我们自己动手设计一个不用电池就能发光的手电筒吧。

10.设计一套调节吊车立柱高度的方案。 你见过建筑工地上的吊车立柱吗？它的升降大有学问。请利用相关知识，设计一套让它随意长高或变矮的方案吧。 +mwSd6IMzy2kMBmlgSszQ8nWUIKr/HIidmPjFBBxS+tmkopUgiLFf/J7eTOvysd7