




让我们来研究以速度 v 沿铁轨行驶的火车上两个特定的点之间的距离。我们知道,测量一段距离,需要有相对于量出这段距离长度的参考物体。在此例中,最简单的参考物体 (坐标系) 是火车本身,在火车上的观察者测量两个特定点之间的距离是用量杆沿一条直线 (例如车厢地板) 一步步量,从一给定的点到另一给定的点需要用量杆测量的次数便是我们所求的距离。
从铁轨线上测量这段距离,与火车上的测量相比,完全是不同的,我们可以考虑使用如下方法。如果我们把火车上的两点称为 A 1 和 B 1 ,那么这两点以速度 v 沿路基移动。首先,我们需要在路基上确定在某一特定时刻,恰好各为由路基判断的 A 1 和 B 1 所通过的两个对应点 A 和 B ,路基上的 A 和 B 点可以用本章 第八节 所提出的时间定义来确定,然后再用量杆沿着路基量取 A、B 两点之间的距离。
以先前的观点来看,我们不能肯定这次的测量结果与第一次的测量结果完全一样。因此,在路基上量出的长度与在火车上量出的长度可能会有不同,这也是我们对本章 第六节 中表面看来是明白的论述提出的第二个不同意见。即:如果车厢里的人在1秒钟内走了一段距离 w ,那么在路基上的话,这段距离并不一定也等于 w 。
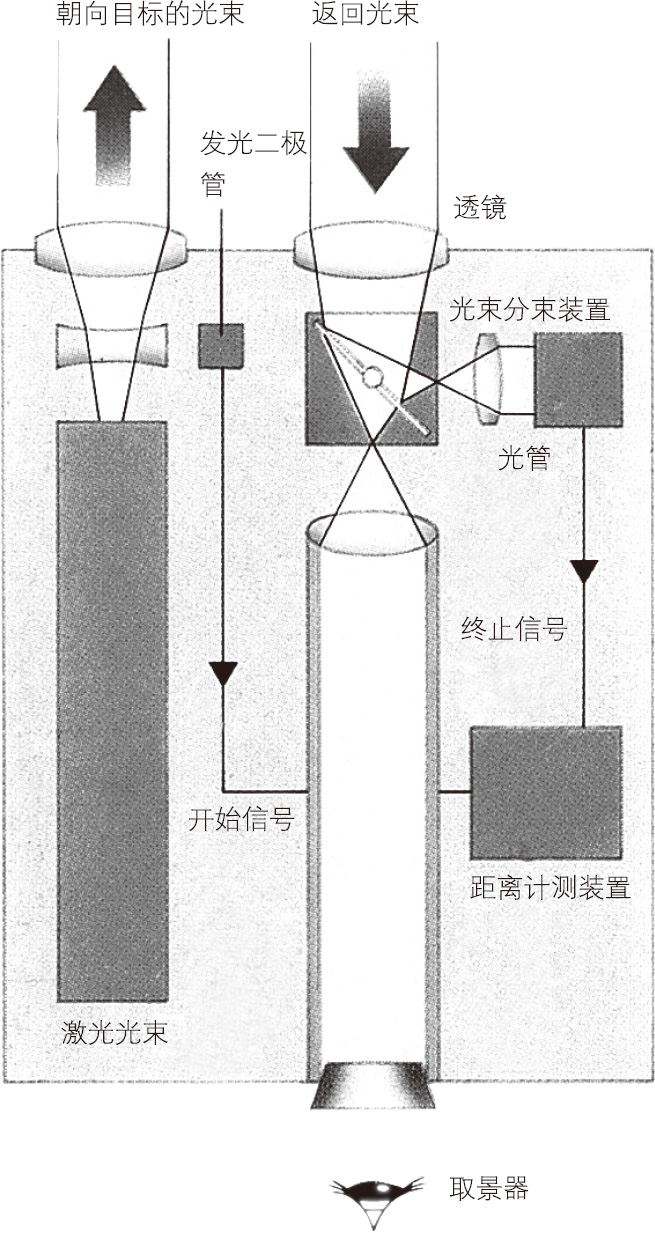
激光测距仪 示意图
激光测距仪是利用激光对目标距离进行准确测定的仪器。激光测距仪在工作时向目标射出一束很细的激光,由光电元件接收目标反射激光束,计时器测定激光束从发射到接收的时间,计算出从观测者到目标的距离。
在本节中,爱因斯坦并没有用物理语言表达他所理解的距离收缩效应。他提出了从铁路线上判断火车上一段距离的“方法”,这种方法与我们建立在绝对时空观基础上的方法没有本质的不同。他可能由于太吝惜笔墨或过高估计了“普通人”的理解能力,以至于没有清楚说明如何用本章 第八节 (“物理学的时间观”) 所提出的时间定义来确定“路基上的 A 点和 B 点”,而依某些人的观点,其本章 第八节 所提出的时间定义与经典物理学的时间定义相比没有什么新鲜之处。他得出了结论:“在路基上量出的长度与在火车上量出的长度可能会有不同。”这确实没错,因为事实上我们这样测量时有时会测得长些、有时又会测得短些,所以,确实很难看出这个描述具有什么实质意义,即很难看出这个描述与长度收缩效应有什么必然联系。因此,爱因斯坦本人是否能物理地理解长度收缩效应,值得怀疑。
《辞海》 (1999年版) 中,“距离”的定义是:①两处相隔,相隔的长度。②几何学的基本概念之一。对不同对象有不同的规定。例如,在欧几里得空间中,两点间的距离是连接这两点的直线段的长。从一点到一直线或一平面的距离是这点向直线或平面所引的垂线段的长;两平行线或平面的距离是指它们间公共垂线段的长。在球面上,两点间的距离是由这两点所确定的大圆的劣弧的长。距离的概念也可以推广到更为一般的数学对象中去。