




平行于同一直线的两条直线相互平行。
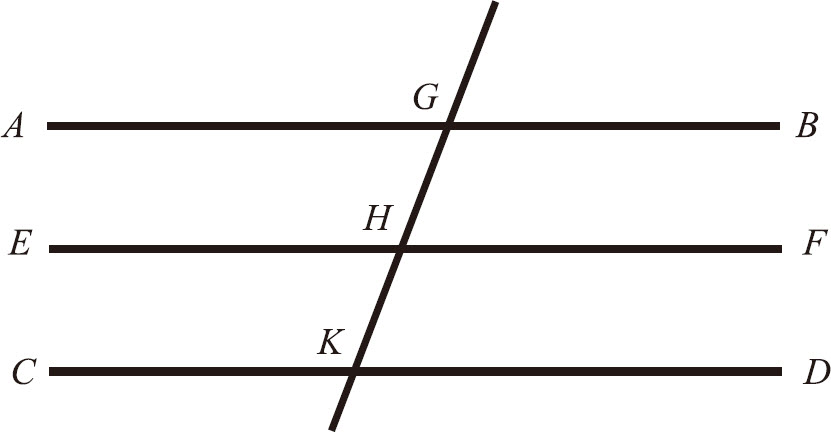
设:线段 AB、CD 平行于 ΕF 。
求证: AB 也平行于 CD 。
令:直线 GK 与它们相交。因为: GK 与平行线 AB、ΕF 相交,∠ AGK 等于∠ GHF (命题I.29) 。
又因为,直线 GK 和平行线 ΕF、CD 相交,∠ GHF 等于∠ GKD (命题I.29) 。
而∠ AGK 也被证明等于∠ GHF ,所以:∠ AGK 也等于∠ GKD (公理I.1) 。且它们是内错角,所以 AB 平行于 CD 。
所以:平行于同一直线的两条直线相互平行。
证完
本命题假设了三条线段位于同一平面内,命题XI.9则是三条线不在一个平面内。
现代综合几何学中,普勒菲尔公理代替了欧几里得的平行公设,该公理陈述,过已知点的一条已知直线至多有一条平行线。
欧几里得的《几何原本》是人类历史上最优美的科学著作之一。刺激我们兴趣的不是那些图形,而是概念——那些相互连接的概念,以及欧几里得所呈现的这些概念及它们的连接方式。《几何原本》的数学优雅,还在于它的简洁与清晰品性,使读者阅读容易、轻松。
对欧几里得批评最多的是平行公设,即I.5公设,其定义含混,没有简洁的品性。本命题也是简洁的,普勒菲尔公理则更为简洁,可以替代I.5公设。
本命题应用在命题I.45和命题IV.7中。