




在任何三角形中,大角总是对大边。
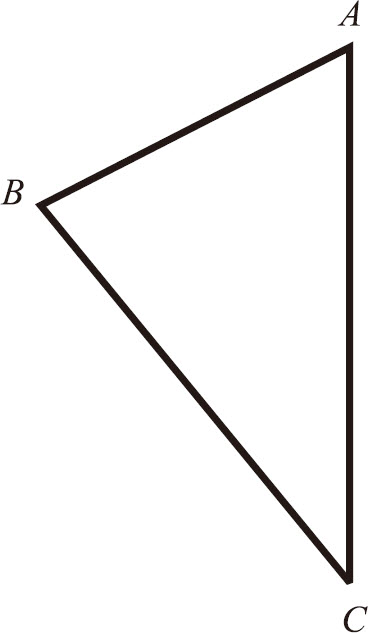
设:三角形 ABC 中∠ ABC 大于∠ BCA 。
求证: AC 边也大于 AB 边。
假设不是,那么 AC 就小于或等于 AB 。
现在我们假设 AC 等于 AB ;那么∠ ABC 就将会等于∠ ACB (命题I.5) 。
但事实并非如此。于是 AC 不等于 AB 。
同理, AC 不能小于 AB ,因为如果这样∠ ABC 也就会小于∠ ACB (命题I.18) 。
但事实也并非如此。所以: AC 不小于 AB 。同时已被证明 AC 不小于 AB 。
所以: AC 大于 AB 。
所以:在任何三角形中,大角总是对大边。
证完
这一命题是前一命题的伪装逆命题。
本命题应用在I.20、I.24中,也应用在卷3的部分命题中。