




一个角可以切分成两个相等的角。
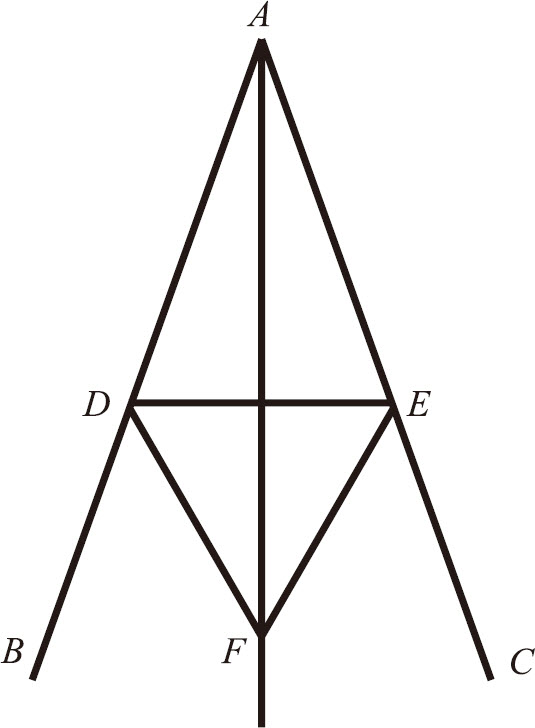
设:已知∠ BAC ,要求二等分这个角。
在 AB 边上任取一点 D ,在 AC 边上取一点 Ε ,使 AΕ = AD (命题I.3) ,连接 DΕ ,以 DΕ 为一边作等边三角形 DΕF ,连接 AF 。
求证:∠ BAC 被射线 AF 平分。
因为, AD 等于 AΕ,AF 为公共边,那么: DA、AF 分别对应 ΕA、AF 并相等。
边 DF 等于边 ΕF ;于是∠ DAF 等于∠ ΕAF (命题I.8) 。
所以:∠ BAC 被射线 AF 平分。
所以:一个角可以切分成两个相等的角。
证完

四面体小行星
这颗小行星是一个正四面体,呈现在我们眼前的是它的其中两个表面。可以看到几乎每一寸土地都得到利用,上面密布了房屋、高塔、桥梁、台阶、花木、人工湖泊和小船;除了形状不同外,其余的情况和地球几乎毫无二致。在作此画时,埃舍尔将两幅草稿拼贴在一起,在面与面的接合处尽量画成直角,以反映四面体的棱线。埃舍尔从事物的数学特性中发掘美,创造出空前绝后的奇妙之作。
构图步骤
当用圆规和直尺构造这一图形时,要求作出三个圆和一个最后的切分线。其中一个圆以 A 点为圆心、 AD 为半径,以决定点 Ε 。另外的两个圆分别以 D 和 Ε 为圆心并以 DΕ 为公共半径。等边三角形在这里实际上是不需要的。
角的三等分
使用欧几里得的直尺和圆规,二等分一个角是容易的,二等分线段也是容易的( 参见命题I.10 ),将线段分成任意数量的相等部分也不那么困难( 参见命题I.9 ),但是将一个角分成相等的奇数部分,就不容易了。事实上,使用欧几里得的工具,就不可能把一个60°的角三等分。欧几里得之前的数学家们为此使用了各种各样的方法,但未成功;欧几里得以后的阿基米德创造了螺旋线,才能将角划分成任意部分,三等分角也就成为可能。人们相信使用欧几里得工具根本就不可能三等分角,但直到1833年,这一疑惑才被数学家旺泽尔所证明。
命题的应用
这一命题被利用在下一命题中,也用在卷4、6、13的数个命题中。
一条线段可以被分成两条相等的线段。

设: AB 为一线段。
求作:平分为两条相等的线段。
作等边三角形 ABC (命题I.1) ,使其∠ ACB 被 CD 线平分 (命题I.9) 。
那么: D 点就是线段 AB 的平分点。
既然 AC 等于 CB,CD 是公共边, AC、CD 两条边分别与 BC、CD 两条边对应相等,∠ ACD 等于∠ BCD ,于是,边 AD 等于边 BD (命题I.4) 。
所以:线段 AB 被 D 点平分。
所以:一条线段可以被分成两条相等的线段。
证完
本命题陈述将线段分成两个相等的部分。
它被利用在本卷的I.12、I.16、I.42中,也被利用在卷2、3、4、10、13的数个命题中。
过一条直线上的一个点,可以作该直线的垂线。

设: AB 是已知直线, C 为直线上的点。
求作:从 C 点作一条直线垂直于 AB 。
令:在 AC 上任取一点 D,CB 上任取一点 Ε ,并让 CD 等于 CΕ (命题I.3) 。
在 DΕ 上作等边三角形 FDΕ (命题I.1) 。连接 FC 。
那么我说: FC 就是直线 AB 在 C 点上的垂线。
因为 DC 等于 CΕ,CF 是公共边,边 DC、CF 分别与边 ΕC、CF 对应且相等;底边 DF 与底边 FΕ 相等;故三角形 DCF 全等于三角形 ΕCF (命题I.8) ,∠ DCF 与∠ ΕCF 互为邻角。
如果一条线段在另一条线段所形成的邻角相等,那么两角皆为直角 (定义I.10) 。所以:∠ DCF 、∠ FCΕ 皆为直角。
所以:线段 CF 垂直于线段 AB ,并在 C 点上平分。
所以:过一条直线上的一个点,可以作该直线的垂线。
证完
这一命题和下一命题陈述垂线,一个给定的(已知的)点向给定的线作垂线。在本命题中,给定的点在直线上,而在下一命题中,是不同的情形。
本命题被利用在本卷的I.13、I.46、I.48中,也用在卷2、3、4、6、11、12、13的数个命题中。