





研究系统动态特性的目的在于深入地了解试验系统的动态响应(即输出),因为系统的输出才是试验所要得到的结果。
对于任何一个试验系统,若输入(也称激励)不同,则输出(响应)亦必然不同。为了便于分析又能全面地了解系统的动态响应,人们常利用简谐、阶跃、脉冲等输入来研究系统的动态响应。
若系统的输入是一个常幅简谐函数,对于线性系统而言,系统的输出一定是同频率、定幅、相位差为 φ 的简谐函数,而且其输出与输入的幅值比相位差正好与对线性系统的微分方程式(2-5)进行傅里叶变换,其输出傅里叶变换与输入傅里叶变换之比(频率响应函数)完全等价,即
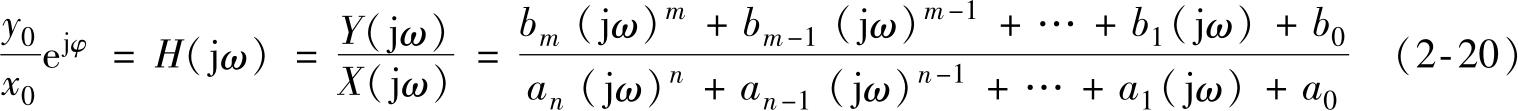
式中 x 0 ——输入的幅值;
y 0 ——输出的幅值;
φ ——输出与输入的相位差;
j=
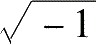 .
.
式(2-20)是复函数,任何复函数均可写成如下形式,即
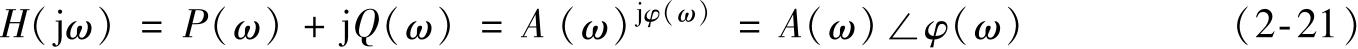
式中 A ( ω )——复函数 H (j ω )的模,其值为:
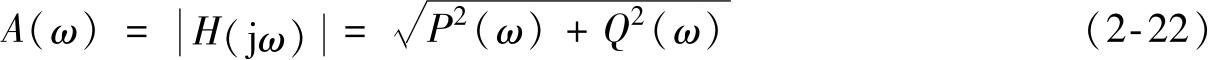
φ ( ω ) ——H (j ω )的相角,其值为:
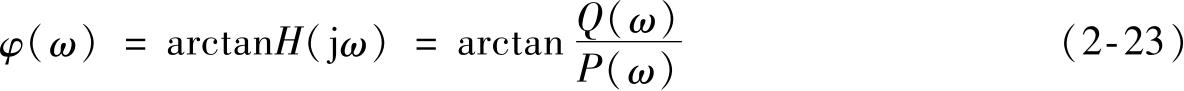
频率响应函数的模 A ( ω )和相角 φ ( ω )均是频率的函数,在工程上常将其分别称为幅频特性和相频特性。在直坐标图上画出的 A ( ω ) -ω 和 φ ( ω ) -ω 曲线分别称为幅频特性曲线和相频特性曲线。对于动态系统,为了方便表达,常将 A ( ω )和 φ ( ω )画在对数坐标中,从而便可得到20lg A ( ω ) -ω 曲线和 φ ( ω ) -ω 曲线,二者统称为伯德图,如图2-8所示。
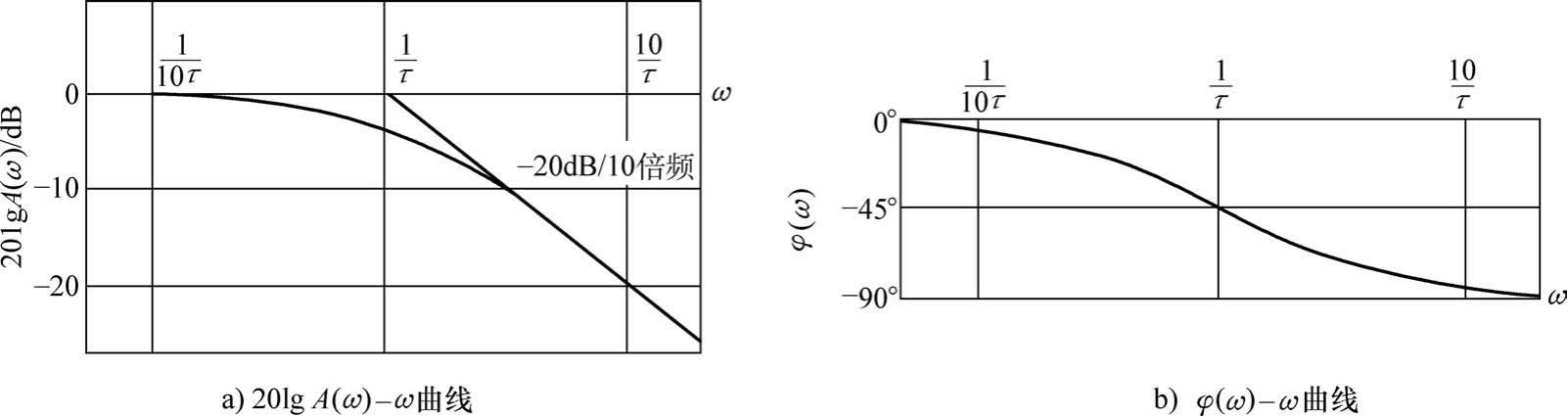
图2-8 一阶系统的伯德图
系统幅频特性和相频特性的另一种作图法是,将频率响应函数的实部 P ( ω )和虚部 Q ( ω )分别作为横坐标和纵坐标,画出它们随 ω 变化的曲线,称为奈奎斯特图,如图2-9所示。图中,自坐标原点到曲线上某一频率点所做的矢量长度便是该频率点的幅值| H (j ω )|,该矢量与横坐标的夹角便是相角 φ ( ω )。
1.一阶系统的频率响应函数
一阶系统的动态数学模型为
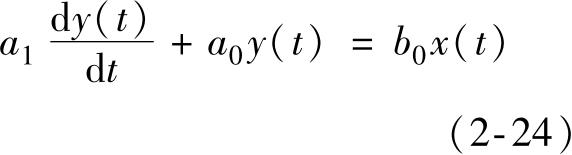
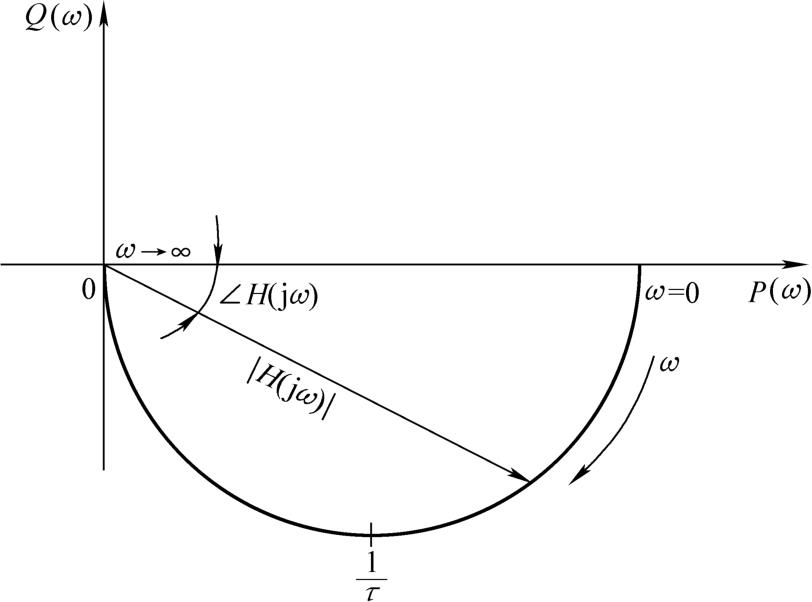
图2-9 试验系统的奈奎斯特图
将等式两边除以
a
0
,并令
E=
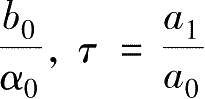 ,得
,得

对式(2-25)做傅里叶变换得
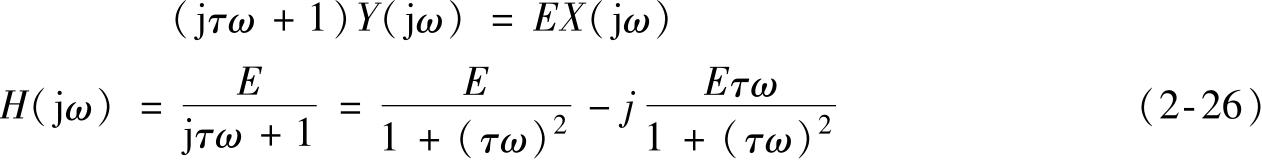
式中 E ——静态灵敏度;
τ ——时间常数。
静态灵敏度 E 是一个只取决于系统结构且与输入无关的常数,它不影响系统动态特性的变化规律,为了分析更加简洁和方便,常设 E= 1,这种处理称为灵敏度归一处理(在后面的分析中,如无特别说明,则均采用灵敏度归一处理)。如此,一阶系统的频率响应函数
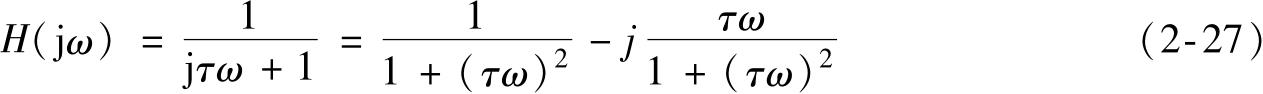
一阶系统的幅频特性和相频特性分别为:
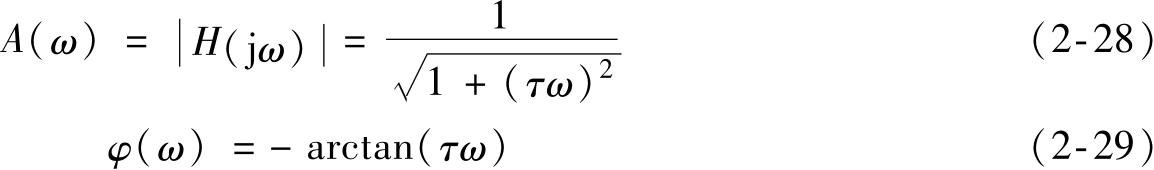
由式(2-20)可知,频率响应函数的模就是输出简谐函数
y
(
t
)的幅值与输入简谐函数
x
(
t
)的幅值比。在灵敏度归一处理的情况下,希望得到的测试结果应该是
A
(
ω
)
=
1,而实际的幅频特性为
A
(
ω
)
=
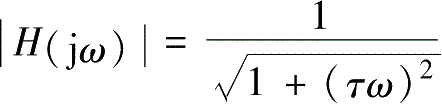 。图2-10是一阶系统的幅频特性和相频特性曲线。当
ω
增加时,响应的幅值逐渐减小,相位差逐渐增大。此外,系统的响应还与时间常数
τ
有关,当
ωτ<
0.3时,振幅与相位的失真均很小,这表明:若系统的时间常数
τ
越小,在系统失真很小情况下的
ω
可以增大,即工作频率范围越宽;反之,
τ
越大,系统的工作频率范围越窄。
。图2-10是一阶系统的幅频特性和相频特性曲线。当
ω
增加时,响应的幅值逐渐减小,相位差逐渐增大。此外,系统的响应还与时间常数
τ
有关,当
ωτ<
0.3时,振幅与相位的失真均很小,这表明:若系统的时间常数
τ
越小,在系统失真很小情况下的
ω
可以增大,即工作频率范围越宽;反之,
τ
越大,系统的工作频率范围越窄。
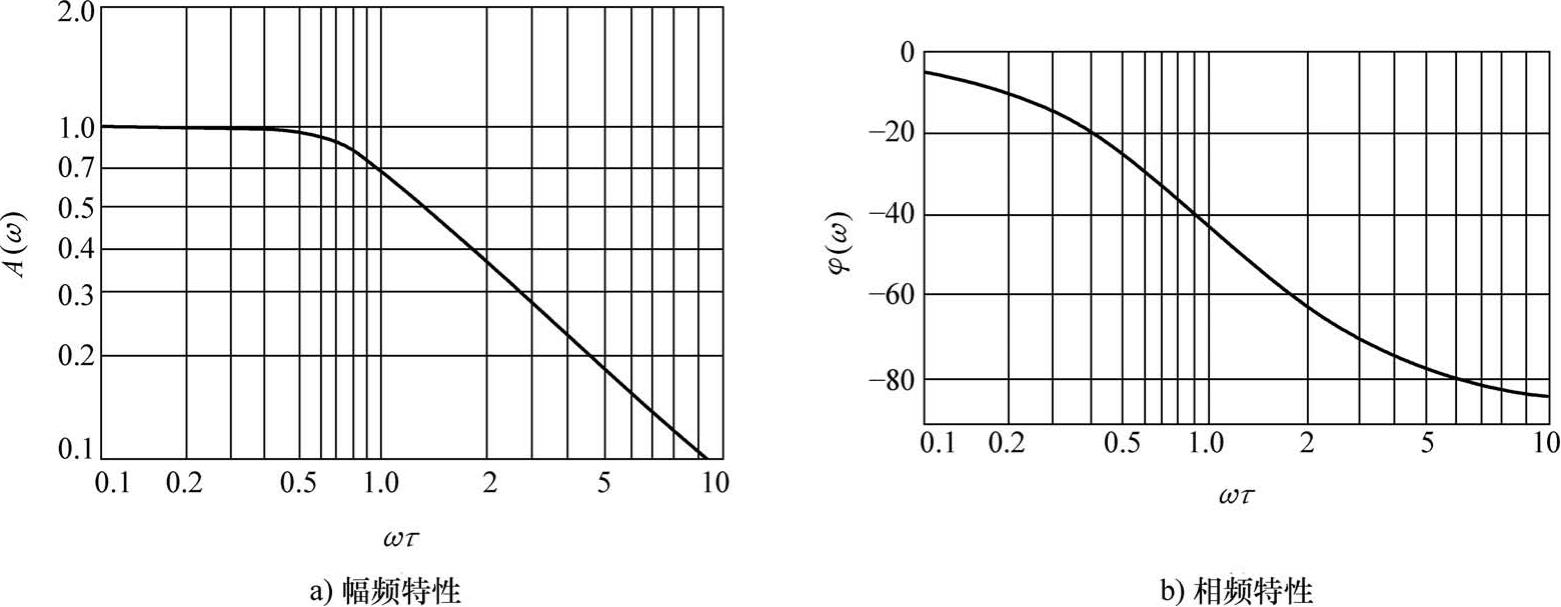
图2-10 一阶系统的频率响应
2.二阶系统的频率响应函数
若式(2-5)中除了 a 2 、 a 1 、 a 0 和 b 0 不为0外,其他各系数均为零,则有
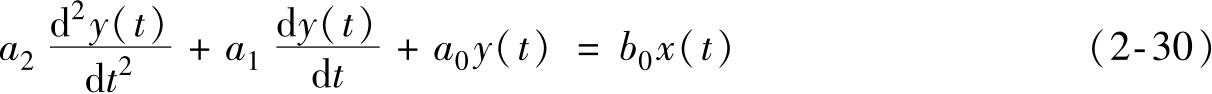
这便是二阶系统的微分方程。
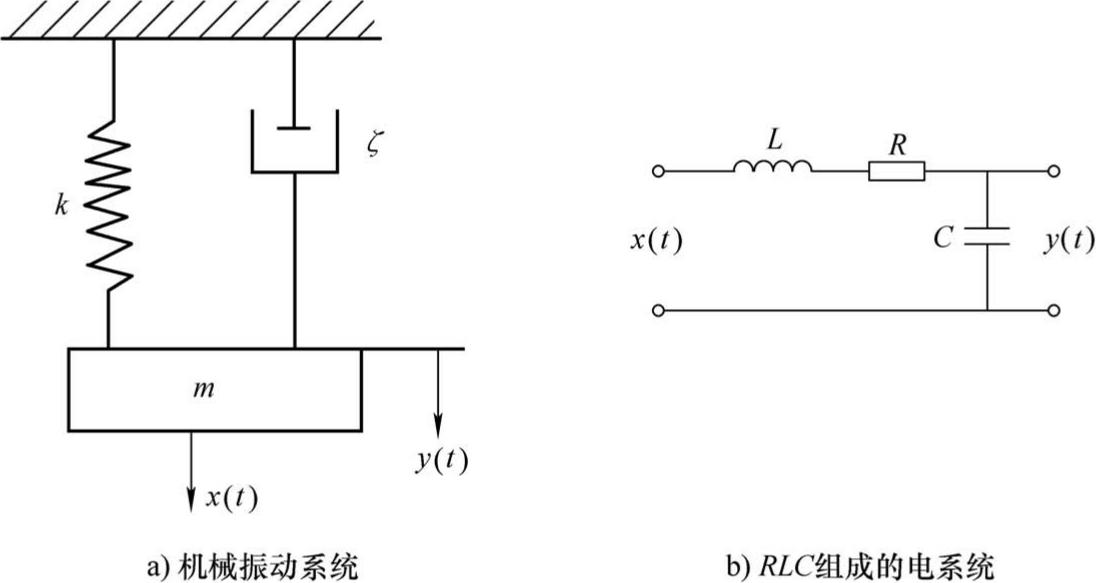
图2-11 实际的二阶系统
图2-11是二阶系统的实例,由弹簧、质量、阻尼组成的机械振动系统和由电阻 R 、电感 L 、电容 C 组成的电系统的微分方程为:
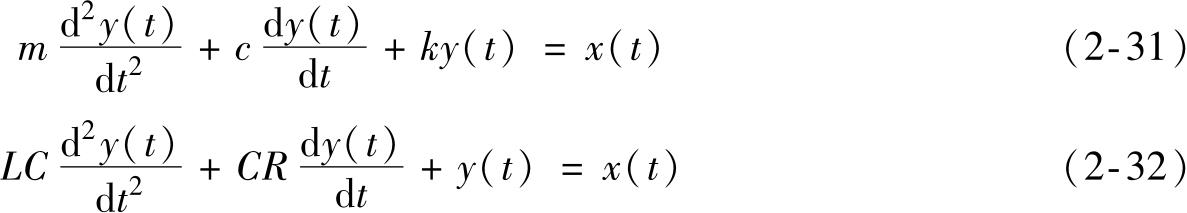
式中 m ——系统的质量;
c ——系统的阻尼系数;
k ——系统的刚度;
R 、 L 、 C ——电阻、电感、电容。
比较式(2-32)和式(2-33)不难发现任意的二阶系统与由弹簧、质量、阻尼组成的机械振动系统具有形式相同的数学模型。下面以机械振动为例分析二阶系统的特征。
令
E
=
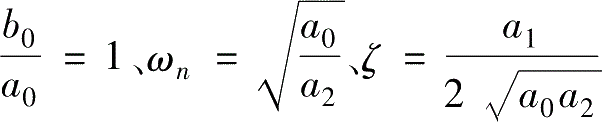 并将其代入式 (2-32)并整理,得
并将其代入式 (2-32)并整理,得
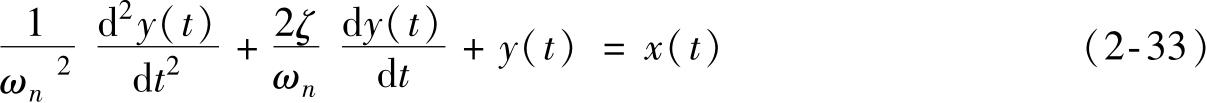
对于上式作拉普拉斯变换,便得到二阶系统的传递函数 H ( s ),即

对式(2-33)做傅里叶变换,可得到二阶系统的频率响应函数 H (j ω )
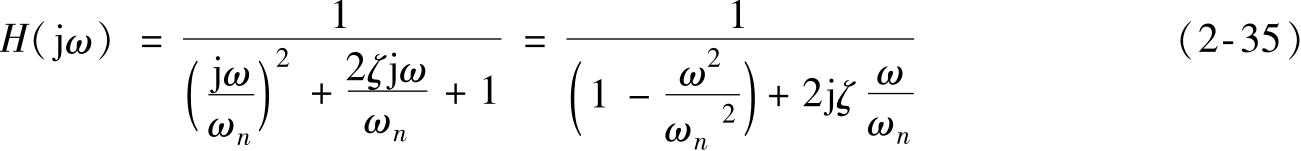
式中
ω
n
——系统的固有频率,
ω
n
=
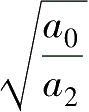 ;
;
ζ
——系统阻尼比,也叫相对阻尼系数,
ζ
=
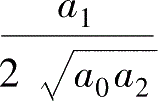 ;
;
ω ——系统振动的圆频率。
由式(2-35)可得到二阶系统的幅频特性和相频特性,即
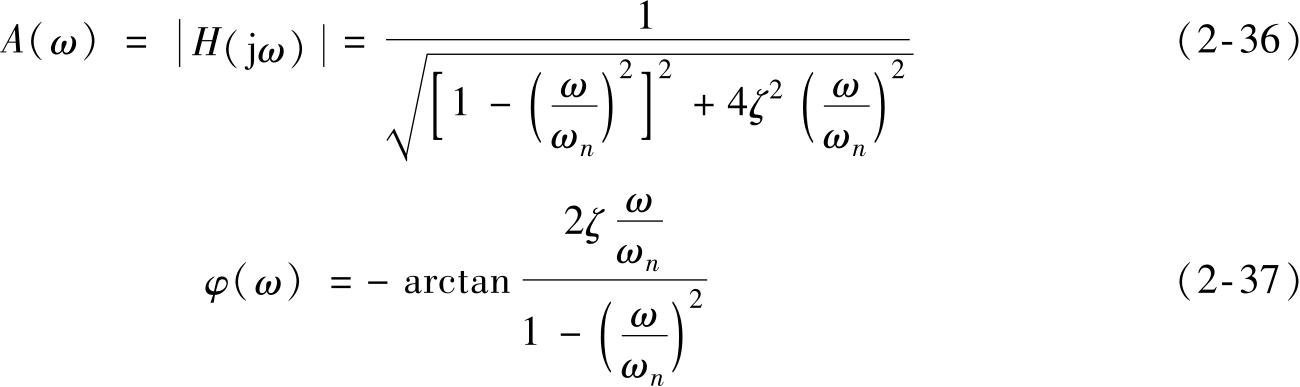
同理,在灵敏度归一处理的情况下,希望得到的测试结果应该是
A
(
ω
)=1,而实际的幅频特性为
A
(
ω
)=
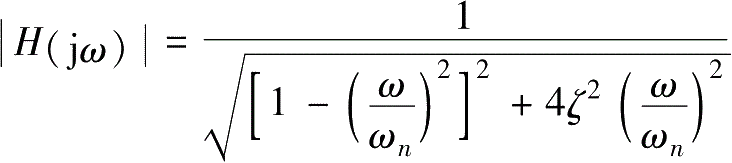 。图2-12和图2-13分别是二阶系统的幅频特性、相频特性和二阶系统的伯德图。
。图2-12和图2-13分别是二阶系统的幅频特性、相频特性和二阶系统的伯德图。
当
ζ
=0时,在
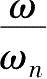 =1附近,输出的幅值显著增加,即当输入的频率与试验系统的固有频率相等时,系统将产生共振。此时,输出与输入的相位差
φ
(
ω
)由0
°
突然变为180°。为了避免此现象的发生,最有效的方法是增加
ζ
;随着
ζ
的增加,在
=1附近,输出的幅值显著增加,即当输入的频率与试验系统的固有频率相等时,系统将产生共振。此时,输出与输入的相位差
φ
(
ω
)由0
°
突然变为180°。为了避免此现象的发生,最有效的方法是增加
ζ
;随着
ζ
的增加,在
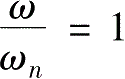 附近,输出的幅值会逐渐减小,但当
ζ
仍较小时,输出的幅值仍会很大,即
A
(
ω
)
>
1;当
ζ
足够大,即
ζ
≥1时,输出的幅值
A
(
ω
)
<
1,系统不会出现共振现象,但在此情况下,
A
(
ω
)≈1的频率范围较小;只有在
ζ=
0.6
~
0.8的范围内,
A
(
ω
)
=
1的频率范围最宽,且
φ
(
ω
)与
附近,输出的幅值会逐渐减小,但当
ζ
仍较小时,输出的幅值仍会很大,即
A
(
ω
)
>
1;当
ζ
足够大,即
ζ
≥1时,输出的幅值
A
(
ω
)
<
1,系统不会出现共振现象,但在此情况下,
A
(
ω
)≈1的频率范围较小;只有在
ζ=
0.6
~
0.8的范围内,
A
(
ω
)
=
1的频率范围最宽,且
φ
(
ω
)与
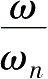 近似线性关系,即系统稳态响应的动态误差最小。由此可见,
ζ
取不同的数值,会对系统的动态响应带来极大的影响。
近似线性关系,即系统稳态响应的动态误差最小。由此可见,
ζ
取不同的数值,会对系统的动态响应带来极大的影响。
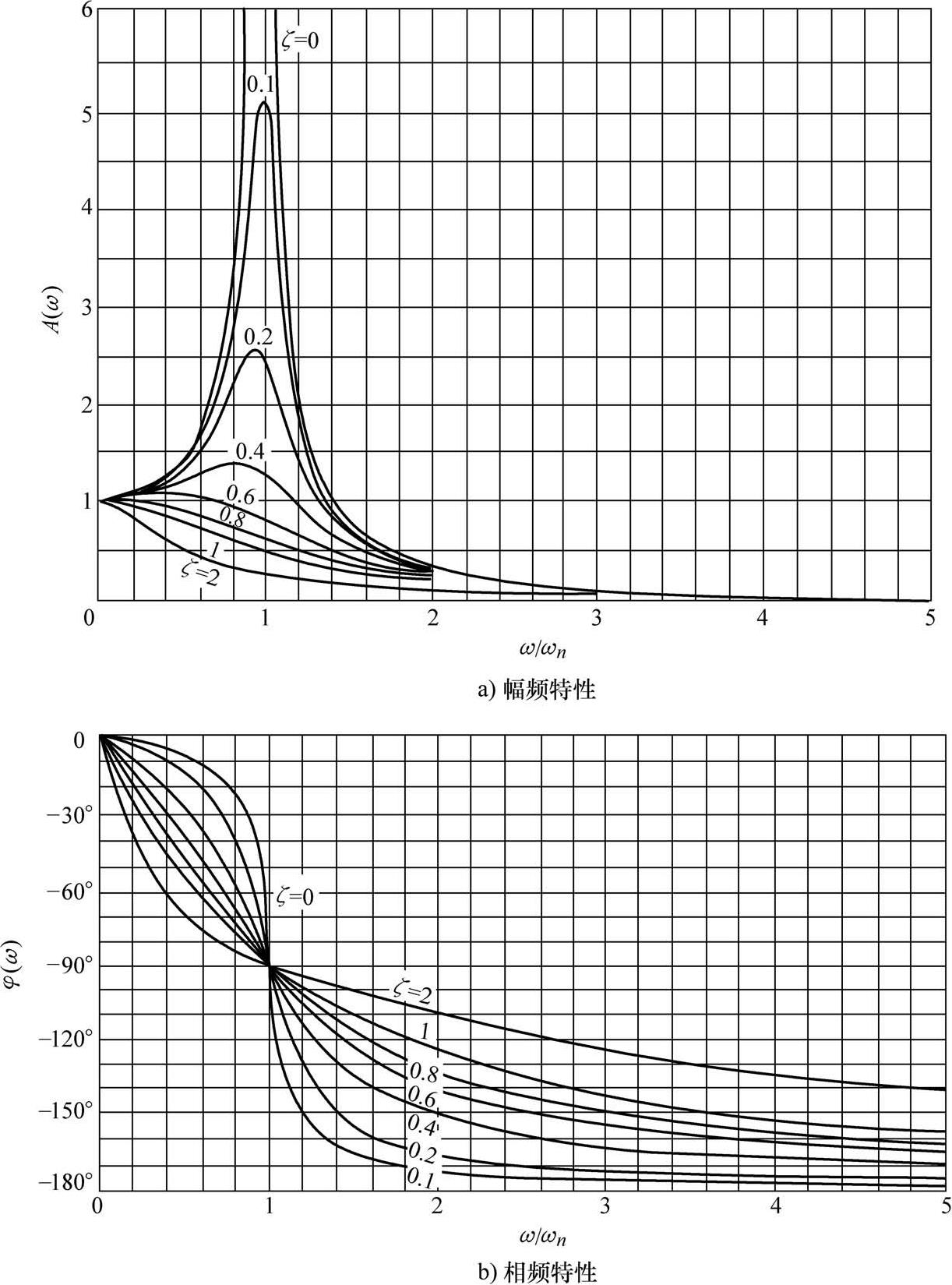
图2-12 二阶系统的幅频和相频特性
系统的阻尼比
ζ
>1,称为过阻尼系统;
ζ
=1,称为临界阻尼系统;
ζ<
1,称为欠阻尼系统。对于欠阻尼系统,由于当
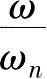 =
1时,系统的输出与输入的相位差
φ=
90
°
,因此可利用这一特点测定系统的固有频率
ω
n
,即:给系统一正弦输入,调节其输入信号的频率,直到输出与输入的相位差
φ
=90°,此时,输入信号的频率
ω
即为系统的固有频率。此测试系统固有频率的方法称为频率共振法。
=
1时,系统的输出与输入的相位差
φ=
90
°
,因此可利用这一特点测定系统的固有频率
ω
n
,即:给系统一正弦输入,调节其输入信号的频率,直到输出与输入的相位差
φ
=90°,此时,输入信号的频率
ω
即为系统的固有频率。此测试系统固有频率的方法称为频率共振法。
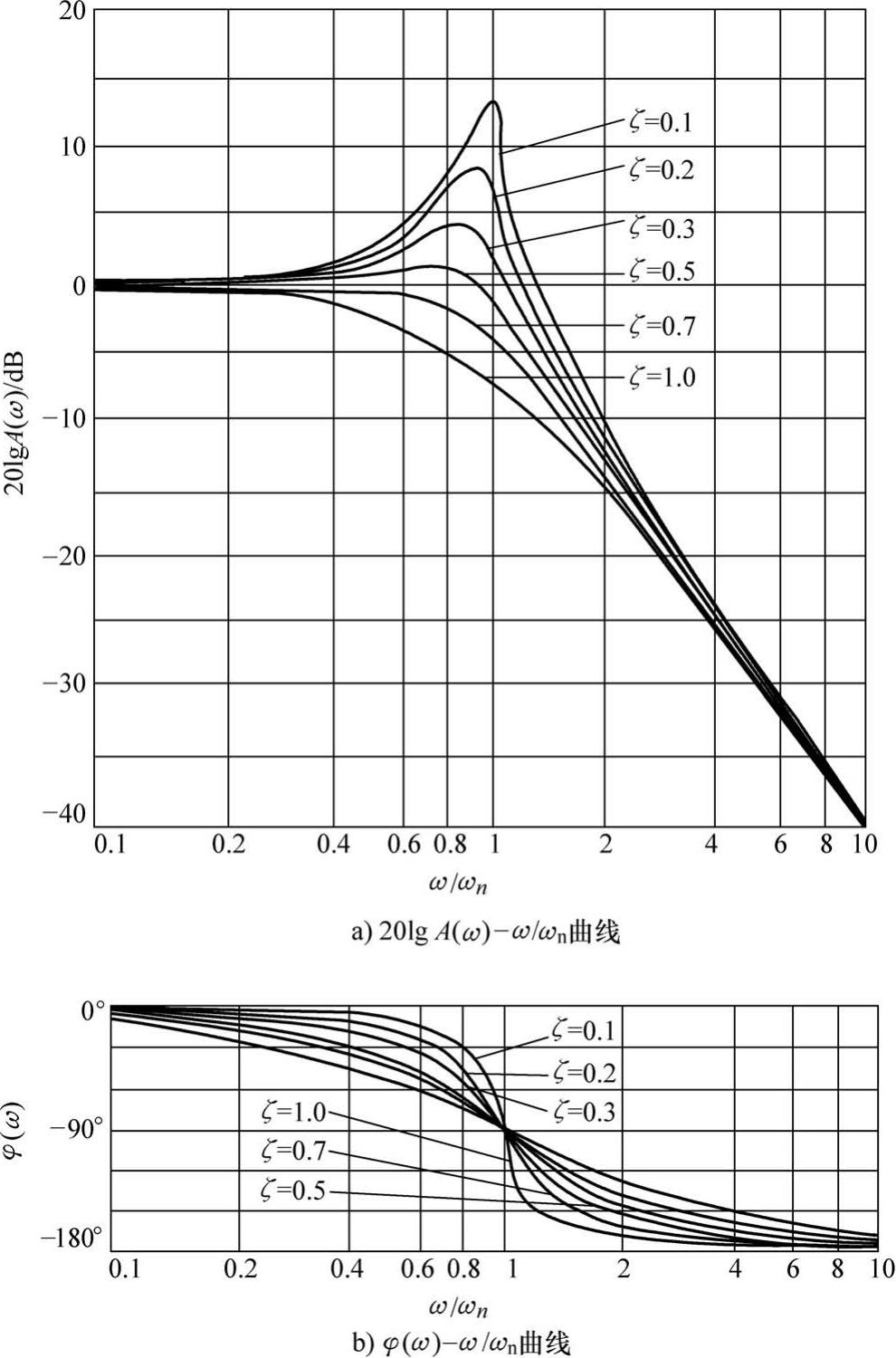
图2-13 二阶系统的伯德图
由图2-12和图2-13还可以看出,在 ζ= 0.6 ~ 0.8时,试验系统固有频率 ω n 越高,动态误差小的工作频率范围越宽;反之, ω n 越低,试验系统的工作频率范围越窄。允许幅值误差所决定的试验系统的工作频率范围称为系统的通频带宽。欲提高试验系统的通频带宽,就应提高系统的固有频率 ω n 。
对于高阶系统可用上述方法对其进行分析。
当给试验系统一阶跃输入时,其系统的输出称为阶跃响应,如对系统突然加载或突然卸载均属阶跃输入。阶跃输入信号是一种常见的基本信号,其输入方式既简便易行,又能充分揭示系统的动态特性。
阶跃输入信号的函数表达式为

式中 A ——阶跃幅值,当 A= 1时称为单位阶跃,工程测试中所谈到的阶跃响应均是指在
单位阶跃输入下系统的响应。
1.一阶系统的阶跃响应
对一阶系统的微分方程式(2-24)进行拉普拉斯变换,并将单位阶跃函数
x
(
t
)的拉普拉斯变换
X
(
s
)
=
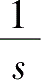 代入其中,整理得
代入其中,整理得

对上式进行拉普拉斯逆变换得一阶系统的阶跃响应函数

在灵敏度归一化( E =1)的情况下,常将系统的输出 y ( t )与输入 x ( t )之差定义为系统的动态误差,用e( t )表示,即
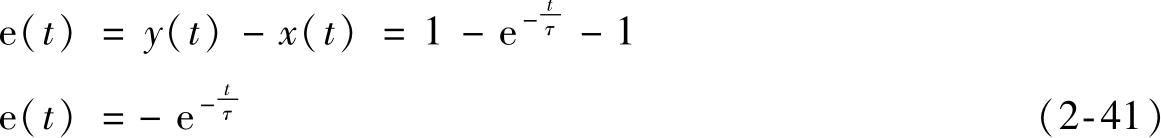
图2-14是一阶系统的阶跃响应曲线和误差曲线。一阶系统阶跃响应曲线的重要特点是:
1)在
t=
0点的切线斜率
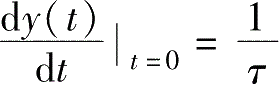 ,据此,在系统参数未知的情况下,由一阶系统阶跃响应的试验曲线可确定其时间常数
τ
;
,据此,在系统参数未知的情况下,由一阶系统阶跃响应的试验曲线可确定其时间常数
τ
;
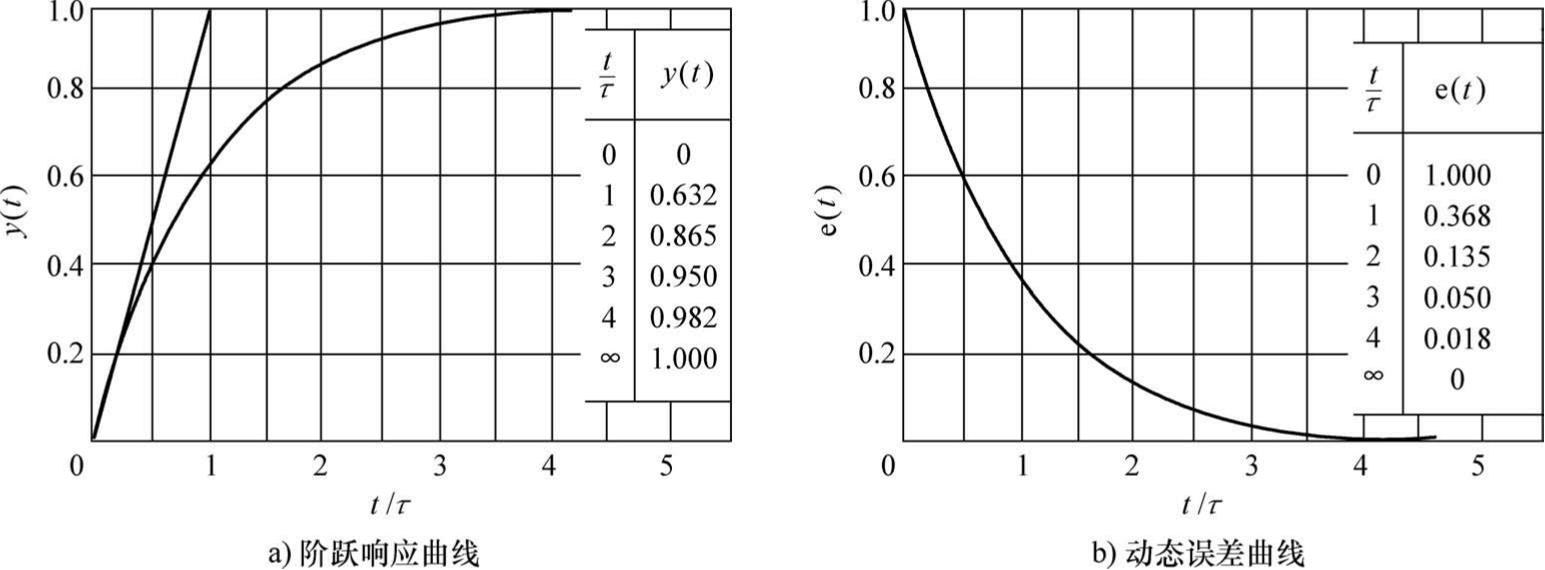
图2-14 一阶系统的阶跃响应和动态误差曲线
2) t= 4 τ 时, y ( t ) = 0.982,此时系统输出值与系统稳态响应值之差不足2%。因此,工程上常将 t= 0 ~ 4 τ 时间段系统的输出称为瞬态, t> 4 τ 时,认为系统已进入稳态。显然,时间常数 τ 越小,系统进入稳态所需的时间就短;反之,系统进入稳态的时间就长。一般来说,一阶系统的时间常数 τ 越小越好。
2.二阶系统的阶跃响应
将前述单位阶跃函数的拉普拉斯变换
X
(
s
)
=
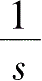 代入二阶系统的传递函数式 (2-34)并整理,得
代入二阶系统的传递函数式 (2-34)并整理,得
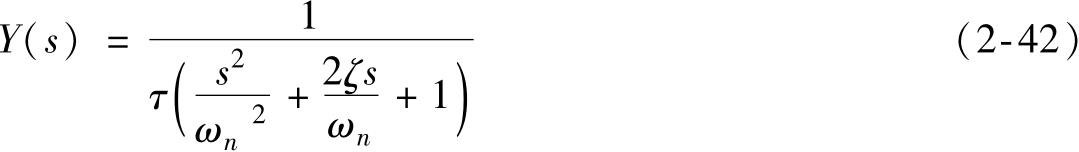
对上式进行拉普拉斯逆变换得
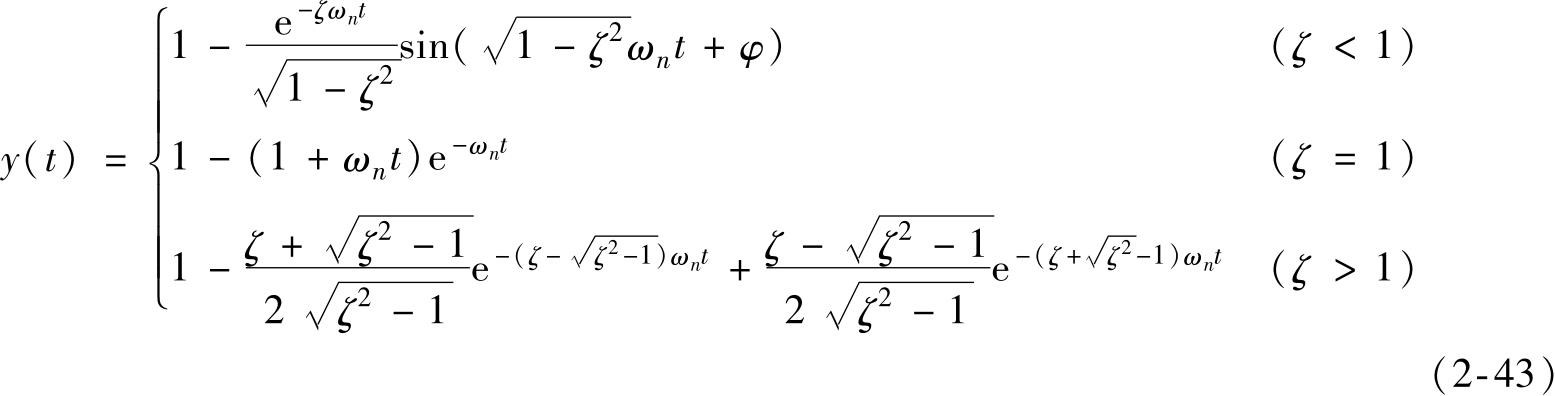
式中
φ
——相位差,
φ=
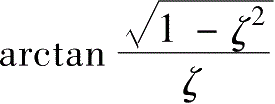 。
。
试验系统的动态误差e( t )为
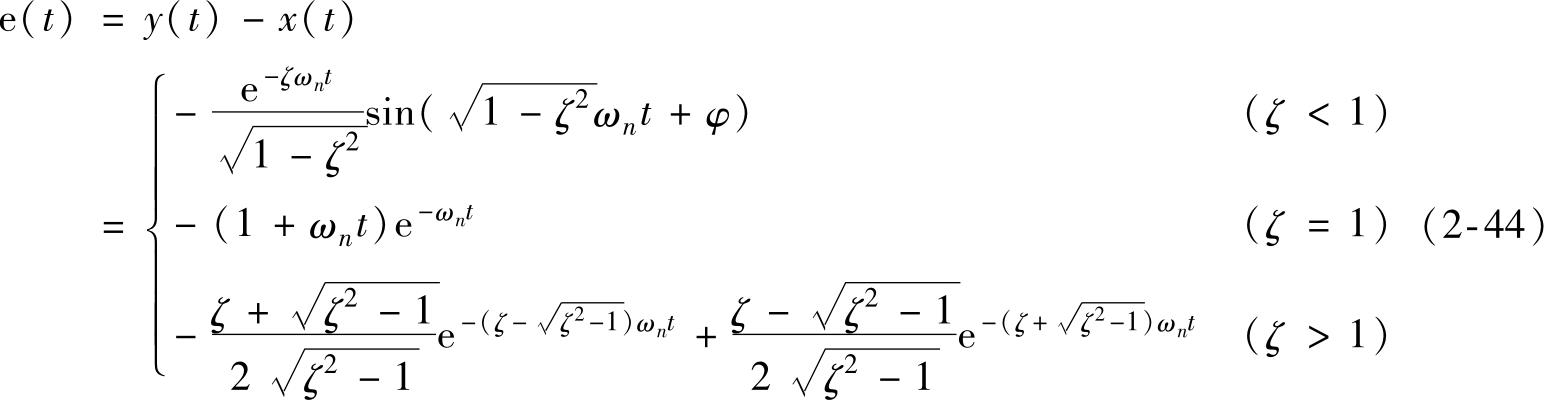
由式 (2-43)和式 (2-44)知,当试验系统的响应时间
t
→∞时,动态误差e(
t
)
=
0,即试验系统没有稳态误差,这一结论对于振动和噪声的测试十分有用。但系统响应在很大程度上由阻尼比
ζ
和固有频率
ω
n
决定,如图2-15所示。系统固有频率
ω
n
越高,系统的响应越快。阻尼比
ζ
直接影响响应的超调量和振荡次数。当阻尼比
ζ=
0时,响应的超调量为100%,系统持续振荡而达不到稳态;当0
<ζ<
1时,随着
ζ
的增大,响应的超调量和振荡次数逐渐减少;当
ζ=
0.6
~
0.8,响应的最大超调量为2.5%~10%,系统达到稳态 (动态误差5%~2%)所需的时间最短,为
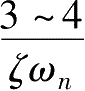 。这就是许多试验系统在设计时,取
ζ=
0.6
~
0.8的重要原因之一;当
ζ>
1时,系统蜕化为两个一阶系统的串联,此时系统虽无超调量 (无振荡),但仍需要较长的时间才能达到稳态。上述结论与二阶系统的频率响应应完全相同。
。这就是许多试验系统在设计时,取
ζ=
0.6
~
0.8的重要原因之一;当
ζ>
1时,系统蜕化为两个一阶系统的串联,此时系统虽无超调量 (无振荡),但仍需要较长的时间才能达到稳态。上述结论与二阶系统的频率响应应完全相同。
用上述分析方法可以得到任意高阶系统的阶跃响应。
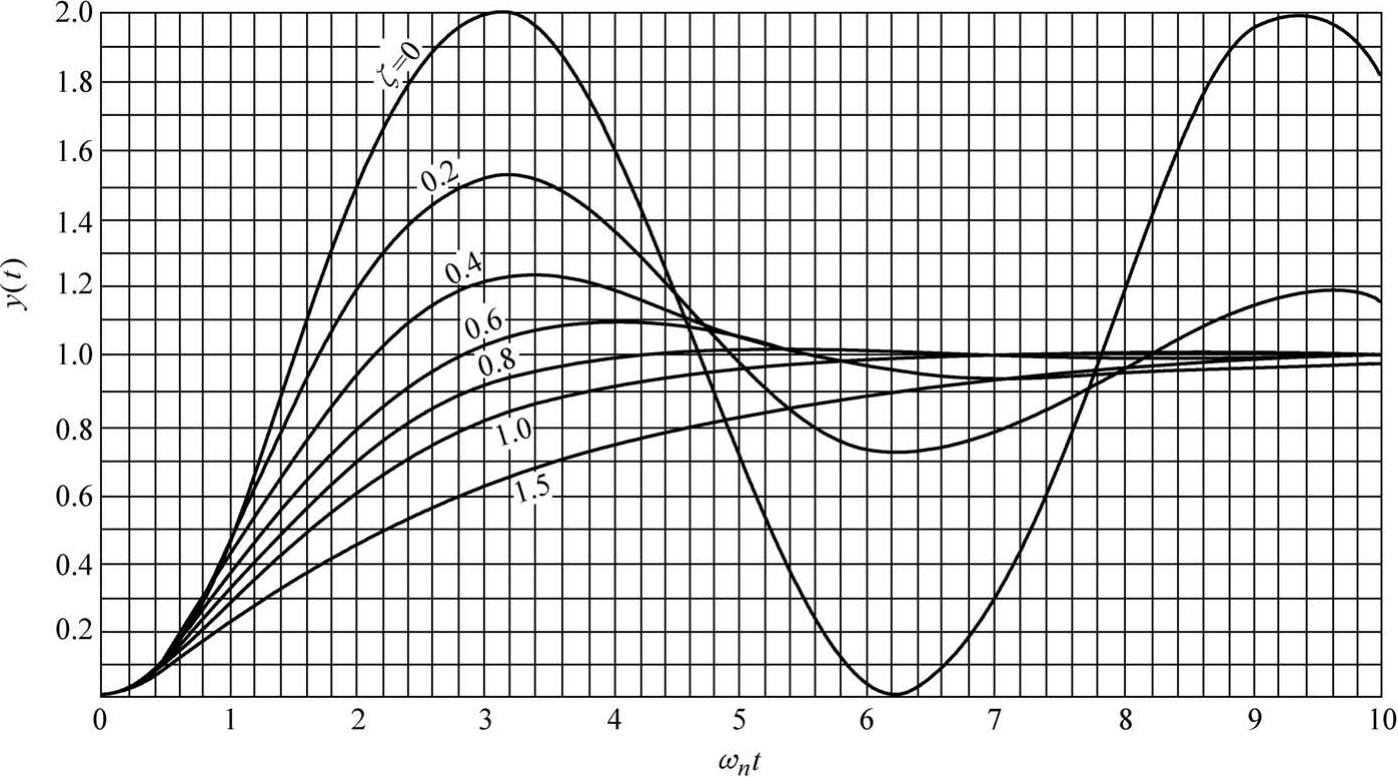
图2-15 二阶系统的阶跃响应
单位脉冲函数的表达式为

单位脉冲函数的傅里叶变换 F [ δ ( t )] = 1,拉普拉斯变换 L [ δ ( t )] = 1。因此,当试验系统的输入为 δ ( t )时,其输出的拉普拉斯变换和傅里叶变换分别为:
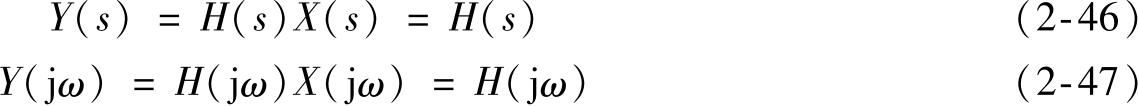
系统的输出或称系统的单位脉冲响应为
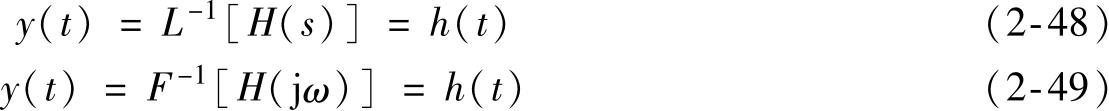
即系统的单位脉冲响应函数 h ( t )与传递函数 H ( s )及频率响应函数互为拉普拉斯变换对和傅里叶变换对。
1.一阶系统的单位脉冲响应
对一阶系统的传递函数
H
(
s
)
=
 进行拉普拉斯逆变换得一阶系统的脉冲响应函数,即:
进行拉普拉斯逆变换得一阶系统的脉冲响应函数,即:

图2-16是一阶系统的单位脉冲响应曲线,曲线揭示了和前面提到的其他典型输入相同的规律。时间常数
τ
大的系统,其响应达到稳态所需的时间就长;反之,响应达到稳态所需的时间就短。当
t=
0时,一阶系统的单位脉冲响应函数
h
(
t
)
=
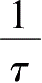 ,据此在系统参数未知的情况下,利用试验所测得的单位脉冲响应曲线可求出时间常数
τ
。当然,由式 (2-45)所给出的单位脉冲函数在实际中是不存在的,工程中常用非常短暂的冲击输入来代替单位脉冲输入,实践表明,当作用时间
,据此在系统参数未知的情况下,利用试验所测得的单位脉冲响应曲线可求出时间常数
τ
。当然,由式 (2-45)所给出的单位脉冲函数在实际中是不存在的,工程中常用非常短暂的冲击输入来代替单位脉冲输入,实践表明,当作用时间
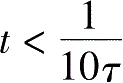 时,则与单位脉冲很接近。
时,则与单位脉冲很接近。
2.二阶系统的单位脉冲响应
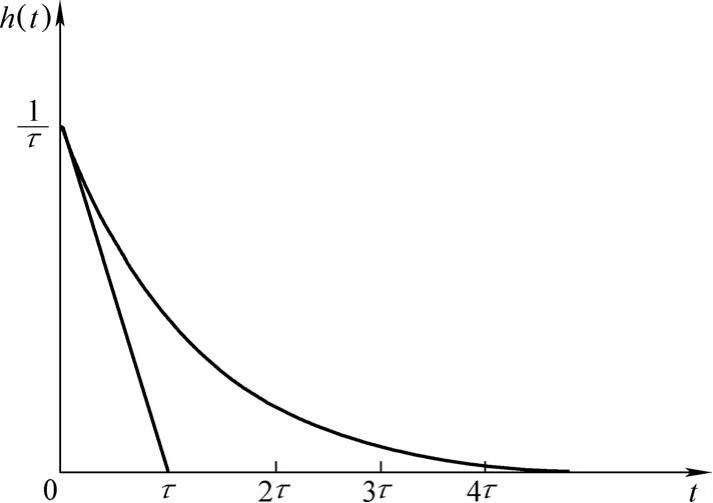
图2-16 一阶系统单位脉冲响应
对式(2-35)进行拉普拉斯逆变换便得到二阶系统的脉冲响应函数 h ( t ),即
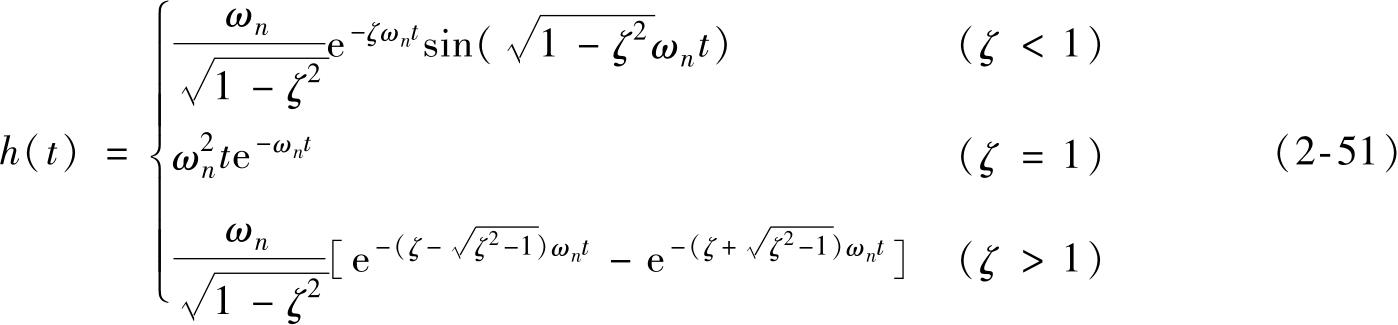
从图2-17中可以看出,当 ζ= 1时,响应无振荡;当 ζ 很小时(如 ζ= 0.1),系统的响应需较长的时间才能进入稳态;当 ζ= 0.65时,响应很快进入稳态。这与前面对其他典型输入信号的响应所显示的规律一致。
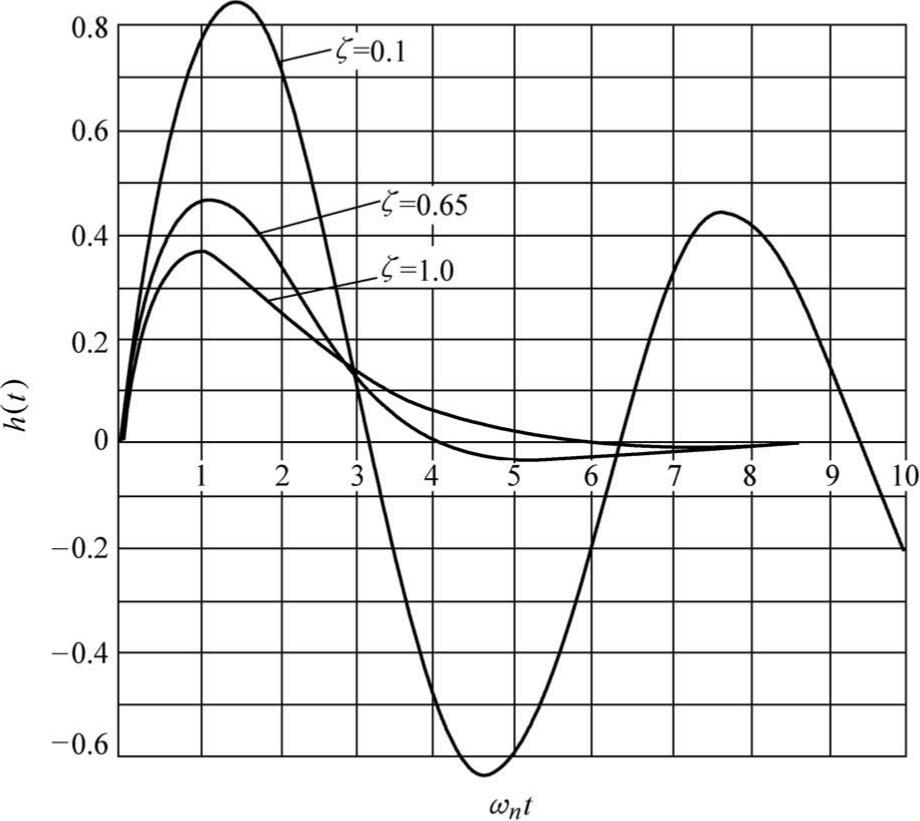
图2-17 二阶系统的脉冲响应函数
从前面对频率响应、阶跃响应及单位脉冲响应的分析中,已了解到时间常数 τ 、阻尼比 ζ 和系统固有频率 ω n 对系统响应的影响,但若要更加深入地认识动态系统,我们有必要对单位斜坡输入下系统的响应进行分析。
单位斜坡函数事实上是单位阶跃函数的积分。由线性系统的积分性可知,单位阶跃响应函数的积分便是单位斜坡响应函数。对式(2-40)和式(2-43)进行积分得到一阶系统和二阶系统斜坡响应函数。
一阶系统的斜坡响应函数为

二阶系统的斜坡响应函数为
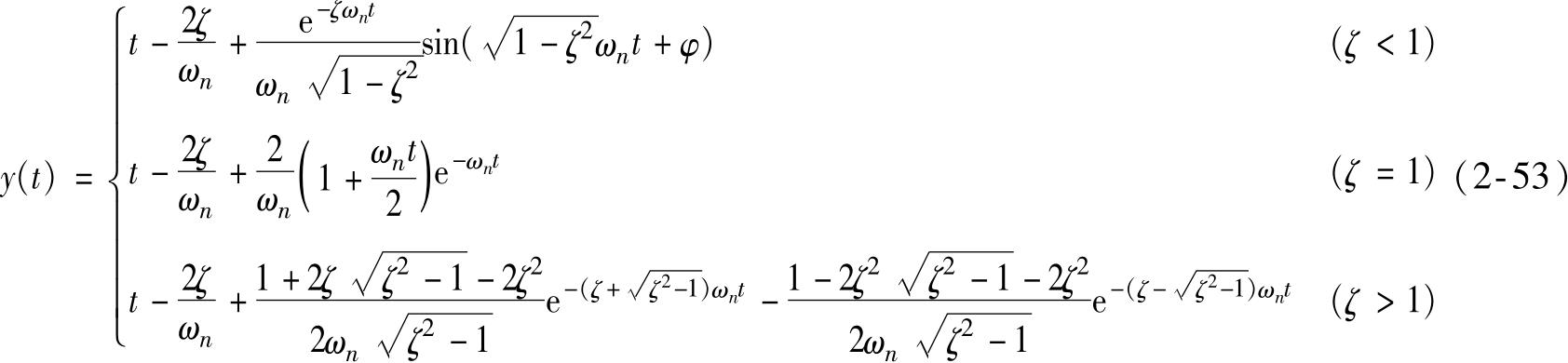
式中
φ
——相位差,
φ=
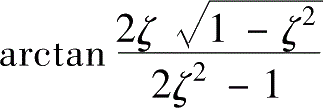 。
。
图2-18是试验系统的斜坡响应曲线。无论是一阶系统还是二阶系统,斜坡响应 y ( t )总是滞后于输入 x ( t )一段时间,即便是系统进入稳态,仍存在动态误差。
从式(2-52)和式(2-53)中可以看出,一阶和二阶系统的斜坡响应函数中均有三项,其中:第一项等于输入 x ( t ),显然第二项和第三项便是试验系统的动态误差。第三项中包含有与时间 t 有关的e -kt 因子,当 t →∞时,此项趋向于零,即该项是系统变化的动态误差,用e s ( t )表示;第二项仅与系统的特性参数 τ 、 ω n 及 ζ 有关,而与时间 t 无关,即系统进入稳态后它仍然存在,而且其数值始终保持不变,故将其称为固定不变的动态误差,又称稳态误差,用e w ( t )表示。如此,式(2-52)和式(2-53)便可改写为如下形式:

式中的稳态误差e w ( t )和变化的动态误差e s ( t )分别为:
一阶系统:
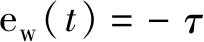
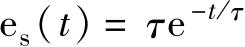
二阶系统
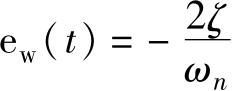
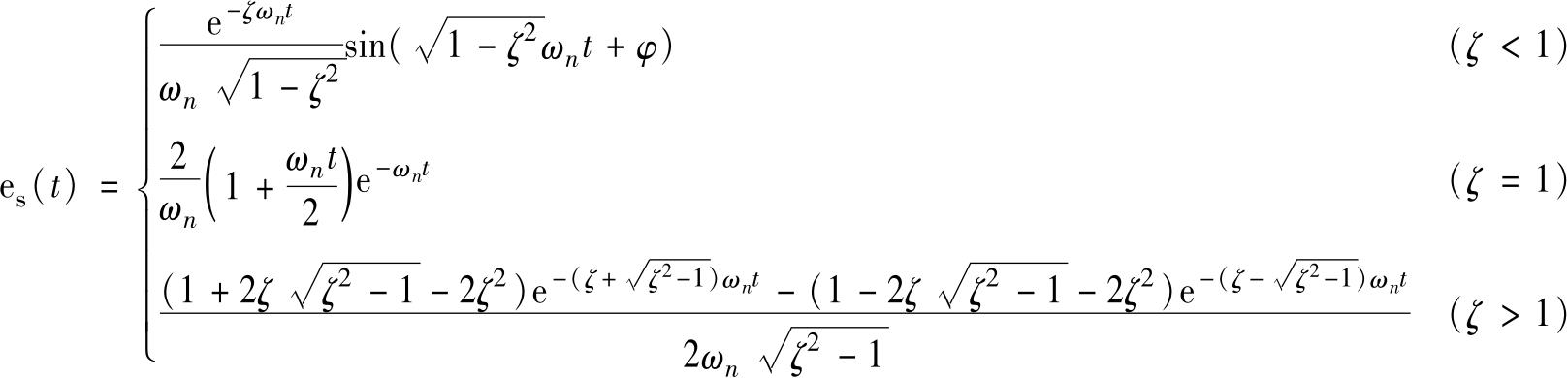
式中
φ
——相位差,
φ=
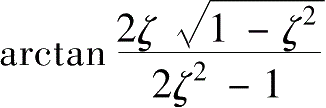 。
。
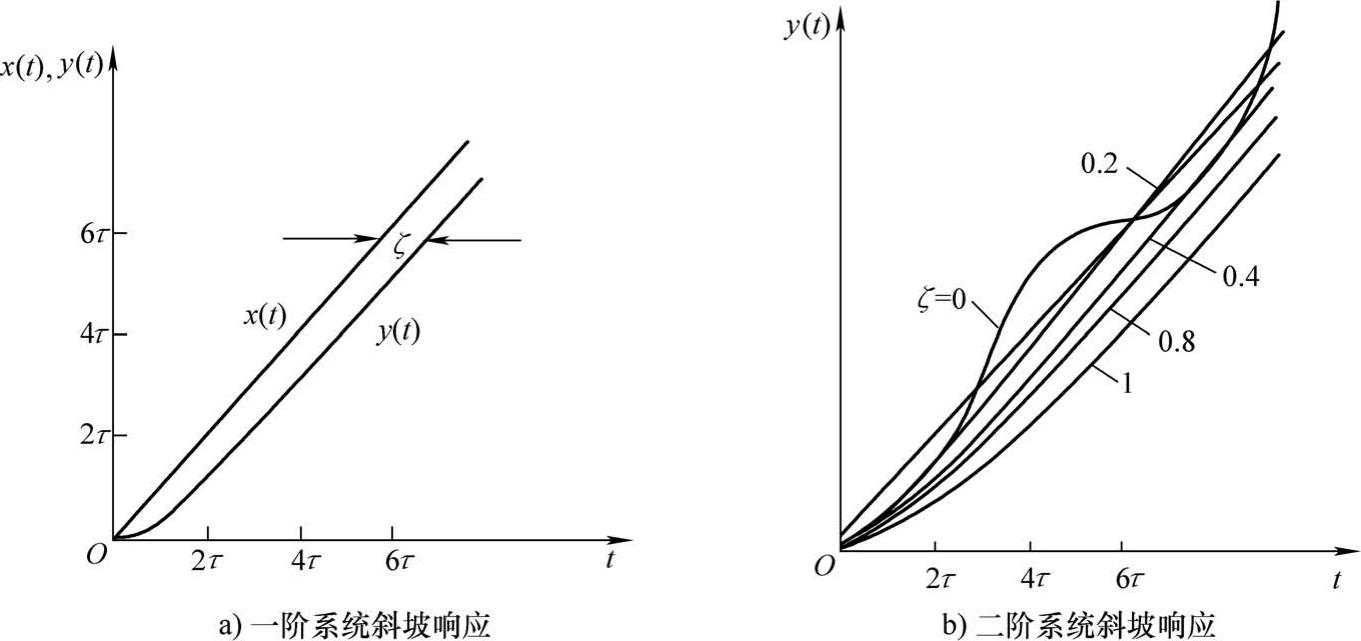
图2-18 试验系统的斜坡响应曲线应
对于斜坡输入的响应,即使系统进入稳态,固定不变的动态误差依然存在,但由于其数值e
w
(
t
)
=
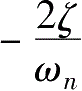 非常小 (由前面的分析可知,试验系统的
ζ
在0.6~0.8之间,固有频率
ω
n
非常大,通常至少在10
5
这样的数量级以上),因此可以忽略。
非常小 (由前面的分析可知,试验系统的
ζ
在0.6~0.8之间,固有频率
ω
n
非常大,通常至少在10
5
这样的数量级以上),因此可以忽略。
对几种典型输入下系统响应的分析,使我们对动态试验系统有了一个深入的了解。在工程实际中,系统的输入很少是上述典型函数,实际输入大多是随机的。为此,我们必须研究任意输入下的系统响应问题。
图2-19是一任意输入信号
x
(
t
),由系统传递函数及频率响应函数的定义式
H
(
S
)
=
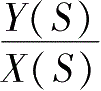 和
H
(j
ω
)
=
和
H
(j
ω
)
=
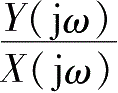 得
得

若能获得传递函数 H ( s )或频率响应函数 H (j ω ),便可利用式(2-55)、式(2-56)求得系统的输入。在工程测试中,用得较多的是频率响应函数,下面就以频率响应函数为例,介绍任意输入下系统输入的计算方法。
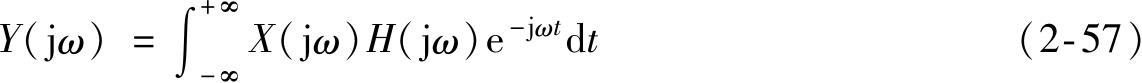
对 Y (j ω )作傅里叶逆变换得到任意输入下的系统响应,即
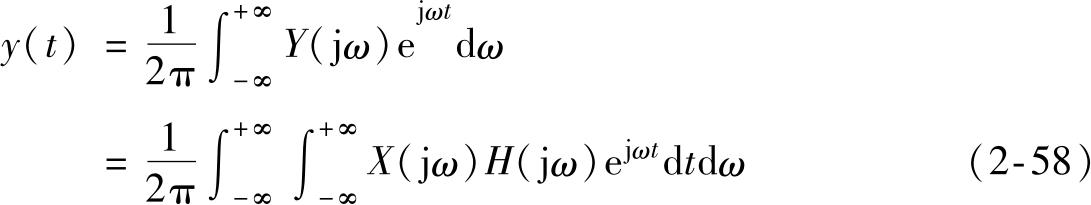
图2-19 任意输入