




弹性力学中经常用到的基本概念包括外力、内力、形变和位移。下面对这些概念加以详细说明。
作用于物体的外力分为体积力和表面力,也分别简称为体力和面力。
所谓体力,是分布在物体体积内的力,例如重力和惯性力。物体内各点受体力的情况一般是不相同的。为了表明该物体在某一点 P 所受体力的大小和方向,在这一点取物体的一小部分,它包含着点 P ,而它的体积为Δ V ,如图2 - 1a所示。设作用于Δ V 的体力为Δ F ,则体力的平均集度为Δ F / Δ V 。如果把所取的那一小部分物体不断减小,即Δ V 不断减小,则Δ F 和Δ F / Δ V 都将不断地改变大小、方向和作用点。现在,令Δ V 无限减小而趋于点 P ,假定体力为连续分布,则Δ F / Δ V 将趋于一定的极限 f ,即
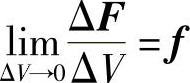
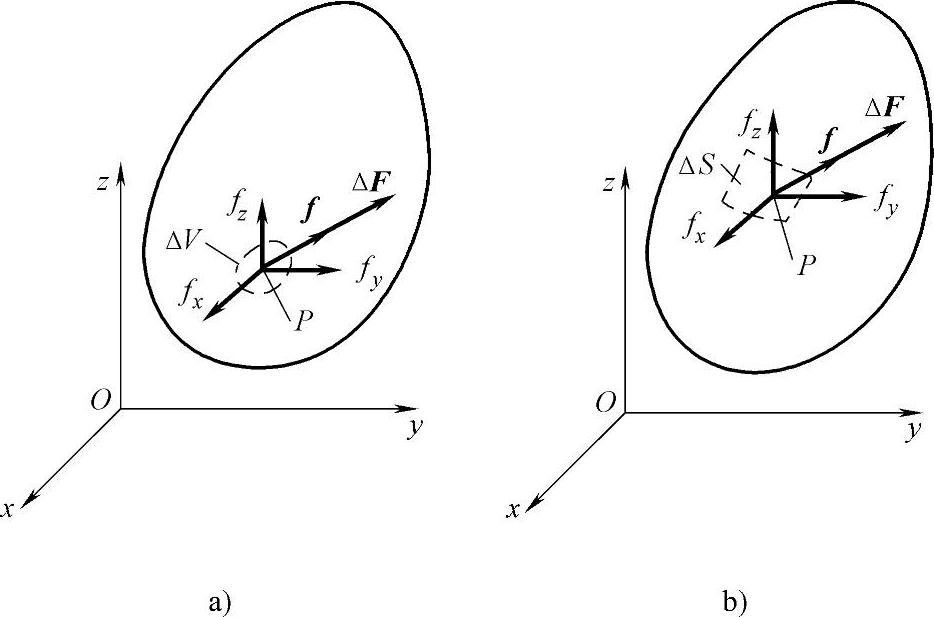
图2 - 1 体力和面力
这个极限矢量限 f 就是该物体在点 P 所受体力的集度。因为Δ V 是标量,所以 f 的方向就是Δ F 的方向。矢量 f 在坐标轴 x 、 y 、 z 上的投影 f x 、 f y 、 f z ,成为该物体在点 P 的体力分量,以沿坐标轴正方向为正,沿坐标轴负方向为负,其量纲是 L -2 MT -2 。
所谓面力,是分布在物体表面上的力。物体在其表面上各点受面力的情况一般也是不同的。为了表明该物体在表面上某一点 P 所受面力的大小和方向,在这一点取该物体表面的一小部分,它包含点 P 且面积为Δ S ,如图2 - 1b所示。设作用于Δ S 的面力为Δ F ,则面力的平均集度为Δ F / Δ S 。与上述相似,令Δ S 无限减小而趋于点 P ,假定面力为连续分布,则Δ F / Δ S 将趋于一定的极限 f ,即
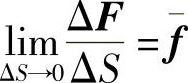
这个极限矢量 f 就是该物体在点 P 所受面力的集度。因为Δ S 是标量,所以 f 的方向就是Δ F 的方向。矢量 f 在坐标轴 x 、 y 、 z 上的投影 f x 、 f y 、 f z ,成为该物体在点 P 的面力分量,以沿坐标轴正方向为正,沿坐标轴负方向为负,其量纲是 L -1 MT -2 。
物体受外力以后,其内部将产生内力,即物体本身不同部分相互作用的力。为了研究物体在其某一点 P 处的内力,假想用经过点 P 的一个截面 mn 将该物体分为Ⅰ和Ⅱ两部分,而将Ⅱ部分撇开,如图2 - 2所示,撇开的部分Ⅱ将在截面 mn 上对留下的部分Ⅰ作用一定的内力。取这一截面的一小部分,它包含点 P 且面积为Δ A ,设作用于Δ A 上的面力为Δ F ,则内力的平均集度,即平均应力为Δ F / Δ A 。令Δ A 无限减小而趋于点 P ,假定内力为连续分布,则Δ F / Δ A 将趋于一定的极限 p ,即
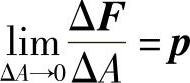
这个极限矢量 p 就是该物体在截面 mn 上点 P 处的应力。因为Δ A 是标量,所以 p 的方向就是Δ F 的极限方向。它与物体的形变和材料强度是直接相关的,应力在其作用截面的法线方向及切线方向的分量,也就是正应力 σ 和切应力 τ ,如图2 - 2所示。应力及其分量的量纲是 L -1 MT -2 。
显然,在物体内的同一点 P ,不同截面上的应力是不同的。为了分析这一点的应力状态,即各个截面上应力的大小和方向,在这一点从物体内取出一个微小的正六面体,它的棱边分别平行于三个坐标轴且长度为 PA =Δ x , PB =Δ y , PC =Δ z ,如图2 - 3所示。
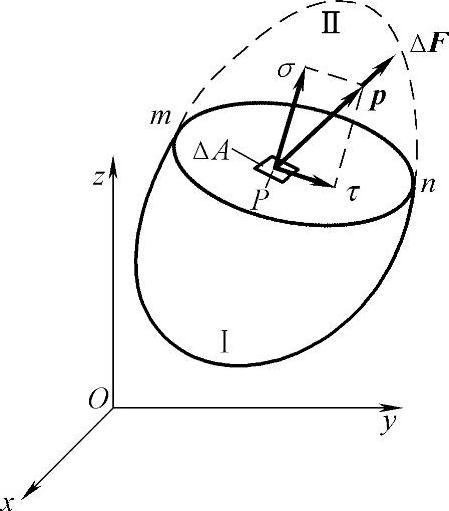
图2 - 2 P 点处的应力
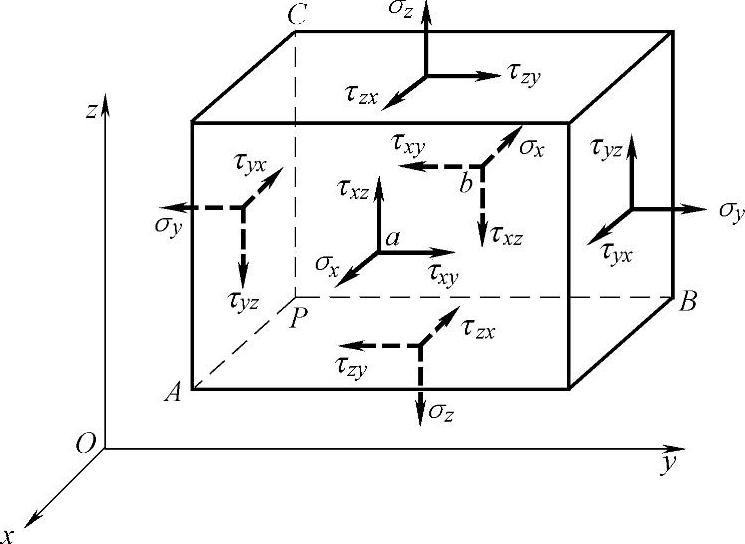
图2 - 3 正平行六面体的应力状态
将每一面上的应力分解为一个正应力和切应力,分别与三个坐标轴平行。正应力用 σ 表示。为了表明这个正应力的作用面和作用方向,加上一个下标字母。例如,正应力 σ x 是作用在垂直于 x 轴的面上,同时也是沿着 x 轴的方向作用的。切应力用 τ 表示,并加上两个下标字母,前一个字母表示作用面垂直于哪一个坐标轴,后一个字母表示作用方向沿着哪一个坐标轴。例如,切应力 τ xy 是作用在垂直于 x 轴的面上且沿着 y 轴方向作用的。
如果某一个截面上的外法线是沿着坐标轴的正力向,这个截面就称为一个正面,这个面上的应力就以沿坐标轴正方向为正,沿坐标轴负方向为负。相反,如果某一个截面上的外法线是沿着坐标轴的负方向,则这个截面就称为一个负面,这个面上的应力就以沿坐标轴负方向为正,沿坐标轴正方向为负。图2 - 3上所示的应力全都是正的。根据力矩平衡方程,可得六个切应力之间的关系: τ xy = τ yx , τ zy = τ yz , τ xz = τ zx 。这就是切应力互等定理:作用在两个互相垂直的面上并且垂直于该面交线的切应力是互等的(大小相等,符号相同)。在物体的任意一点,如果已知 σ x 、 σ y 、 σ z 、 τ yz 、 τ zx 和 τ xy 这六个应力分量,就可以求得经过该点的任意截面上的正应力和切应力。因此,上述六个应力分量可以完全确定该点的应力状态。
所谓形变,就是形状的改变。物体的形状总可以用它各部分的长度和角度来表示。因此,物体的形变总可以归结为长度和角度的改变。
为了分析物体在某一点 P 的变形状态,在这一点沿着坐标轴 x 、 y 、 z 的正方向取三个微线段 PA 、 PB 、 PC 。物体变形之后,这三个线段的长度以及它们之间的夹角一般都将有所改变。各线段的每单位长度的伸缩,称为线应变,亦称正应变;各线段之间的夹角的改变,用弧度表示,称为角应变。线应变用字母 ε 表示,如 ε x 表示 x 方向的线段 PA 的线应变。
线应变以伸长时为正,缩短时为负,与正应力的正负号规定相适应。切应变用字母 γ 表示:如 γ xy 表示 x 和 y 两方向的线段( PA 与 PB )之间夹角的改变。切应变以夹角变小时为正,变大时为负,与切应力的正负号规定相适应。在物体的任意一点,如果已知 ε x 、 ε y 、 ε z 、 γ yz 、 γzx 和 γxy 这六个应力分量,就可以求得经过该点的任意线段的线应变,也可以求得经过该点的任意线段之间的角度的改变。因此,上述六个应变,称为该点的形变分量,可以完全确定该点的形变状态。
所谓位移,就是位置移动。物体内任意一点的位移,用它在 x 、 y 、 z 三轴上的投影 u 、 v 、 w 来表示,以沿坐标轴正方向为正,沿坐标轴负方向为负。这三个投影称为该点的位移分量。位移及其分量的量纲是 L 。
一般而论,弹性体内任意一点的体力分量、面力分量、应力分量、形变分量和位移分量,都是随着该点的位置而变的,因而都是位置坐标的函数。
由于工程实际问题的复杂性,导致弹性力学方程未知量的求解困难重重,实际上也不可能求解。因此,必须分清主次因素,按照所研究物体的性质以及求解问题的范围,在建立力学模型时,概括出决定固体材料弹性形变的本质因素,提出建立宏观形变基本规律的若干基本假定,略去一些影响很小的次要因素,使得在此基础上建立起来的力学计算模型既符合客观实际,又便于数学方法的有效处理,从而使所导出的本构方程的求解成为可能,使研究的问题限制在一个方便可行的范围之内。这对于弹性力学分析是十分必要的。在今后的问题讨论中,如果没有特别的提示,均采用以下的弹性力学基本假定。
(1)连续性假定 假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。这样,物体内的一些物理量,如应力、形变、位移等,才可能是连续的,因而才可能用坐标的连续函数来表示它们的变化规律。实际上,一切物体都是微粒组成的,严格来说都不符合上述假定;但是可以想见,只要微粒的尺寸以及相邻微粒之间的距离都比物体的尺寸小得很多,那么关于物体连续性的假定,就不会引起显著的误差。
(2)完全弹性假定 假定物体是完全弹性的。所谓弹性,指的是“物体在引起形变的外力被除去以后能恢复原形”这一性质。所谓完全弹件,指的是物体能完全恢复原形而没有任何剩余变形。这样的物体在任一瞬时的形变就完全取决于它在这一瞬间所受的外力,与过去的受力情况无关。在一般的弹性力学中,完全弹性的这一假定,表明形变和引起形变的应力两者之间是呈线性关系的,这种线性的完全弹性体中应力和应变之间服从胡克定律,其弹性常数不应随应力或形变的大小而改变。
(3)均匀性假定 假定物体是均匀的,即整个物体是由同一材料组成的。这样,整个物体的所有部分才具有相同的弹性,因而物体的弹性才不随坐标位置而变。如果物体是由两种或两种以上的材料组成的,只要每一种材料的颗粒远远小于物体而且在物体内均匀分布,这个物体就可以当做均匀的。
(4)各向同性假定 假定物体是各向同性的,即物体的弹性在所有各个方向都相同。这样,物体的弹性常数才不随方向而变。
(5)小变形假定 假定物体发生小变形,即物体位移和形变是微小的。假定物体受力以后,整个物体所有各点的位移都远远小于物体原来的尺寸,而且形变和转角都远小于1。这样,在建立物体变形以后的平衡方程时,就可以方便地用变形以前的尺寸代替变形以后的尺寸,而不致引起显著的误差;并且,在考察物体的形变与位移的关系时,转角和应变的二次和更高次幂或乘积相对于其本身都可以略去不计。因此,弹性力学里的几何方程和平衡微分方程都可简化为线性方程。在上述这些假定下,弹性力学问题都化为线性问题,从而可以利用叠加原理。