习题

一、单项选择题

（A）

1．设 f （ x ）在 x = a 处可导，则 =（　）．

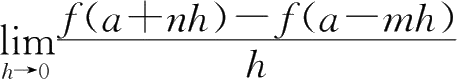A． f' （ a ）

B． mf' （ a ）

C． nf' （ a ）

D．（ m + n ） f' （ a ）

2．设 f （ x ）=（ x +1）（ x +2）……（ x +50），则 f' （-1）=（　）．

A．50！

B．-50！

C．49！

D．-49！

3．若 y = f （ x ），有 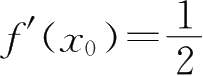，则当Δ x →0时，在点 x = x ₀ 处的微分d y 是（　）．

A．与Δ x 等价无穷小

B．与Δ x 同阶无穷小，但不是等价无穷小

C．比Δ x 高阶无穷小

D．比Δ x 低阶无穷小

4．设 y =（sin x ） ^x ，则 f' （ x ）=（　）．

A．（cos x ） ^x

B．（sin x ） ^x

C．（sin x ） ^x （lnsin x + x cot x ）

D．（sin x ） ^x （lnsin x - x cot x ）

5．设 y = x e ^{- x} ，则 f'' （ x ）=（　）．

A．e ^{- x}

B．（1- x ）e ^{- x}

C．（2- x ）e ^{- x}

D．-（2- x ）e ^{- x}

6．设 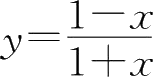，则 f'' （ x ）=（　）．

A．2（1+ x ） ^-2

B．-2（1+ x ） ^-2

C．4（1+ x ） ^-3

D．-4（1+ x ） ^-3

7．设 ，则d y =（　）．

A．

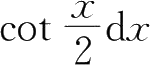
B．

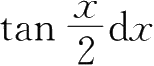
C．

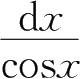
D．

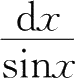
8．设 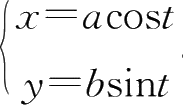，则 =（　）．

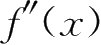A．

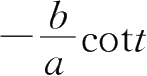
B．

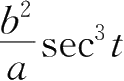
C．

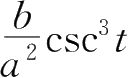
D．

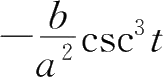
9．设 f （ x ）在（ a ， b ）内连续，且 x ₀ ∈（ a ， b ），则在点 x ₀ 处（　）．

A． f （ x ）的极限存在，且可导

B． f （ x ）的极限存在，且不一定可导

C． f （ x ）的极限不存在

D． f （ x ）的极限不一定存在

10．曲线 y =2 x ² +3 x -26上点 M 处的切线斜率为15，则点 M 的坐标是（　）．

A．（3，15）

B．（3，1）

C．（-3，15）

D．（-3，1）

11．设 f （ x ）= k sin x -2 x ，且 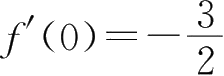，则 k =（　）．

A．1

B．

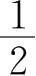
C．

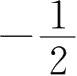
D．0

12．函数 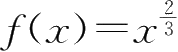在点 x =0处（　）．

A．连续不可导

B．可导不连续

C．可导

D．不可导不连续

13．设 f （ x ）= x ³ ln x ，则 f' （ x ）等于（　）．

A．3 x

B． x ² （3ln x +1）

C．3 x ² ln x

D．4 x ²

14．设 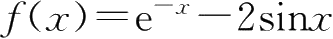在 x =0处可导，则极限 =（　）．

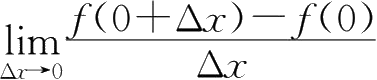A．3 f' （0）

B．-3 f' （0）

C．1

D．-3

15．函数 y = x +e ^x ，其反函数 x = φ （ y ）的导数为（　）．

A． x +e ^x

B．

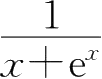
C．

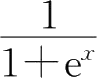
D．1+e ^x

16．设 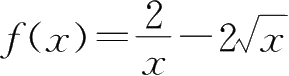，则d f （ x ）=（　）．

A．

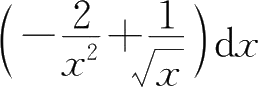
B．

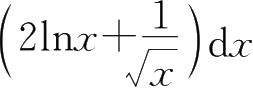
C．

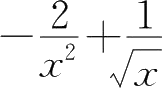
D．

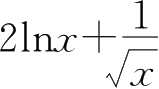
17．若 y = f （ x ）在点 x ₀ 处的增量为 f （ x ₀ +Δ x ）- f （ x ₀ 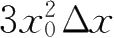）= +3 x ₀ （Δ x ） ² +（Δ x ） ² ，则 y = f （ x ）在点 x ₀ 处的微分d y _{x = x 0} =（　）．

A．0

B．3Δ x

C．3 x ₀ Δ x

D．

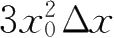
18．设 y = x ⁿ +2 ^x ，则 y ^{（ n +1）} =（　）．

A．（ n +1）！+（ln2） ^{n +1} 2 ^x

B．（ n +1）！+ln2·2 ^x

C． n ！ +2 ^x

D．（ln2） ^{n +1} 2 ^x

19．已知 y = f （ x ）为可导函数，且 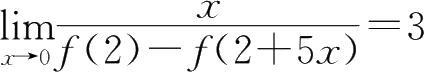，则 f' （2）=（　）．

A．-

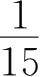
B．

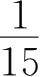
C．-15

D．15

20．若dln（1+ x ）= f （ x ）darctan 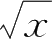，则 f （ x ）=（　）．

A．1

B．2 x

C．

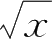
D．2

（B）

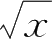
21．已知 f （ x ）在点 x =0处可导，且 f （0）=0，则 =（　）．

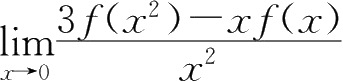A．- f' （0）

B． f' （0）

C．2 f' （0）

D．∞

22．若 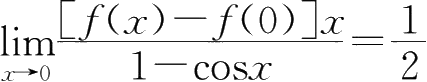，则 f' （0）=（　）．

A．不存在

B．1

C．

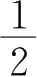
D．

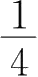
23．设 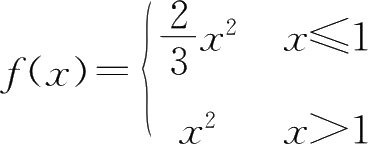，则 f （ x ）在点 x =1处的（　）．

A．左、右导数都存在

B．左导数存在，但右导数不存在

C．左导数不存在，但右导数存在

D．左、右导数都不存在

24．设 f （ x ）为连续函数，且 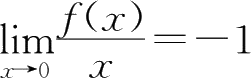，则曲线 y = f （ x ）上对应 x =0处切线方程为（　）．

A． y =2

B． y =2 x

C． y = x +1

D． y =- x

25．设函数 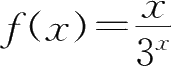，则 =（　）．

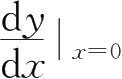A．-1

B．0

C．1

D．2

26．曲线 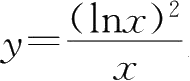上其切线平行于 x 轴的点为（　）．

A．（e ² ，4e ^-2 ）

B．（e ² ，0）

C．（1，1）

D．（1，e）

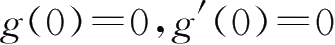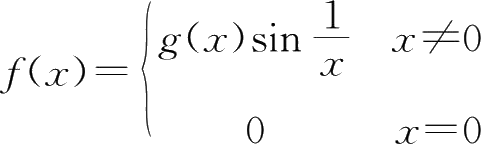27．已知 ，且 ，则 f' （0）=（　）．

A．不存在

B．0

C．1

D．-1

28． =（　）．

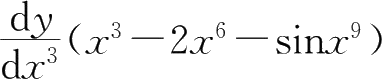A．3 x ² -12 x ⁵ -cos x ⁹

B．3 x ² -12 x ⁵ -9 x ⁸ cos x ⁹

C．1-4 x ³ -cos x ⁹

D．1-4 x ³ -3 x ⁶ cos x ⁹

29．设函数 f （ x ）在 x =2的某领域内可导，且 f' （ x ）=e ^{f （ x ）} ， f （2）=1，则 f‴ （2）=（　）．

A．0

B．e ³

C．2e ³

D．1

30．设函数 y =1+e ^{- x} 的一阶导数 f' （ x ）存在且不为零，其反函数为 x = φ （ y ），则 φ' （ y ）=（　）．

A．

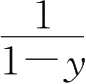
B．

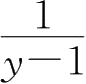
C．

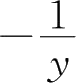
D．-e ^{- x}

二、填空题

1． f （ x ）可导，则 =（　）．

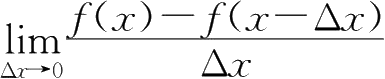2． y =ln sin ² x ， y' =（　）．

3．设 y = f [cot（ x ² ）]，其中 f （ x ）是可导函数，则d y =（　）．

4．设 y ³ = x ² +6 x - y ² ，则 y' =（　）．

5．设 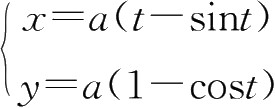，则 =（　）．

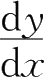6．设 f （ x ）可导， y = f （e ^x ），则d y =（　）．

7．设 f （ x ）=sinsin x ，则d f （ x ）=（　）．

8．曲线2 x ² -2 y + y ³ =1，在（1，1）处的切线斜率为（　）．

9．设e ^y + xy =e，求 y'' =（　）．

10．函数 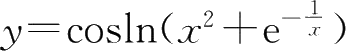的微分d y =（　）．

三、判断题

1．若曲线 y = f （ x ）处处有切线，则 y = f （ x ）必处处可导．（　）

2．若 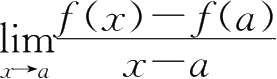= A （ A 为常数）， f （ x ）在点 x = a 处连续．（　）

3．若函数 y = f （ x ）在点 x ₀ 处可导，则| f （ x ）|在点 x ₀ 处一定可导．（　）

4．初等函数在其定义域内一定可导．（　）

5．若 y = f （ x ）在（- a ， a ）内可导且导数为奇函数（偶函数），则 f （ x ）在该区间内为偶函数（奇函数）.（　）

6．若 y = f （ x ）在点 x ₀ 处可微，则 f （ x ）在点 x ₀ 处也一定可导．（　）

7．连续是可导的充分条件．（　）

8．若 y =（cos x ） ^x ，则 y' = x （cos x ） ^{x -1} .（　）

9．在微分学中，Δ y =d y ，Δ x =d x .（　）

10． y =| x -1|在 x =1处可微．（　）

四、计算及证明题

（A）

1．求下列函数的导数．

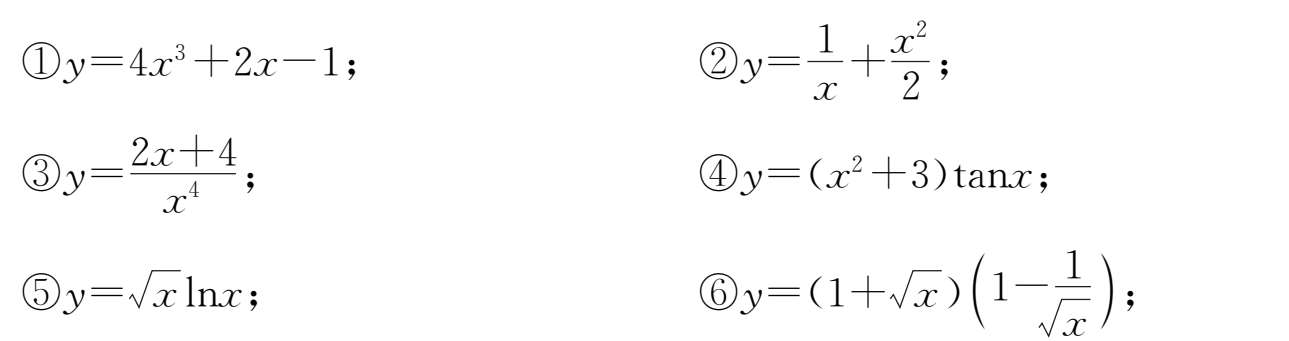
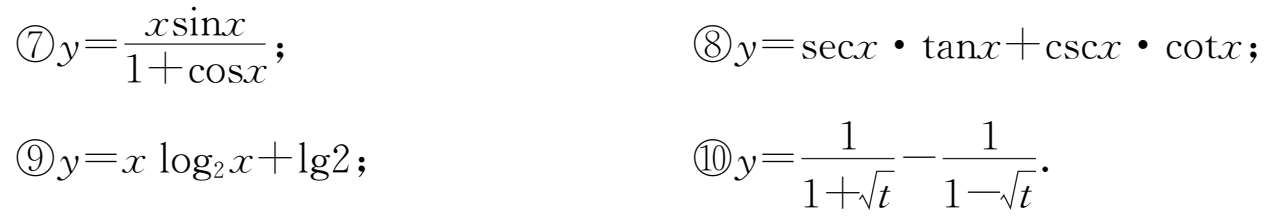
2．设 f （ x ）=cos x ·sin x ，求 ．

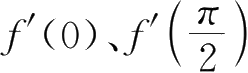3．设 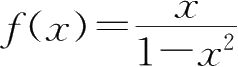，求 f' （0）、 f' （2）．

4．求曲线 y =4 x ² +4 x -3在（1，5）点处的切线和法线方程．

5．物体运动方程为 s = t +sin t ，求物体运动的速度和加速度．

6．求下列各函数的导数．

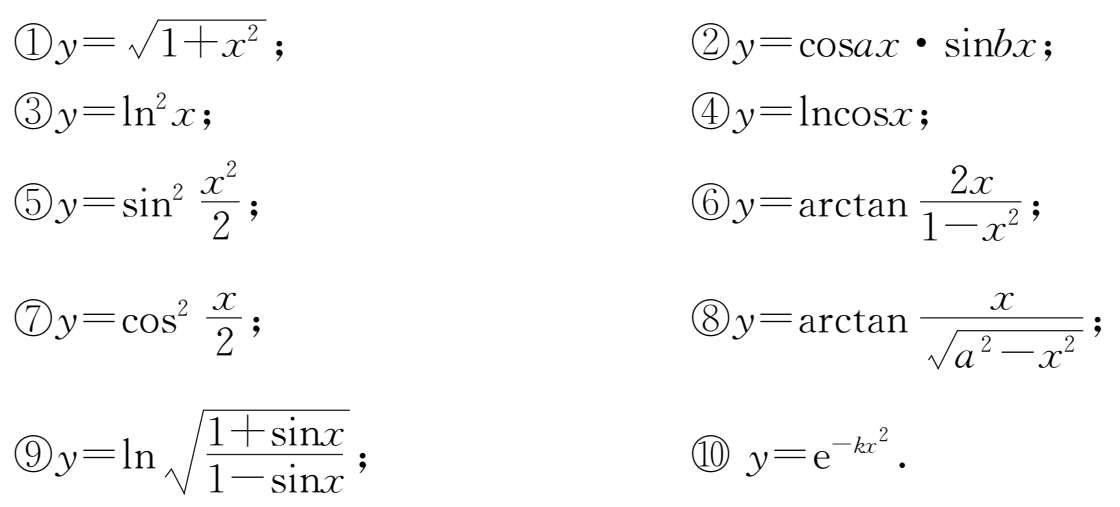
7．求下列各隐函数的导数．

① y ² = apx ；　　　② x ² + y ² - xy =1；

③ x ³ + y ³ -3 axy =0；　　　④ y =1- x e ^y ．

8．取对数求下列各函数的导数．

① xy = 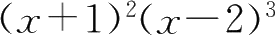；　　　②

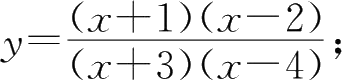
③ y ^x = x ^y ；　　　④e ^y = xy ．

9．求下列各函数的二阶导数．

① y =e ^x sin x ；　　　② y = x ² e ^{- x} ；

③ y =2 x ² +ln x ；　　　④ y = a cos bx ．

10．某物体降温过程中的温度为 u = u ₀ e ^{- kt} ，求物体的冷却速率．

11．口服某药物后，血药浓度为 C （ t ）= a （e ^{- kt} -e ^{- mt} ），求血药浓度的变化率．

12．一截面为倒置等边三角形的水槽，长20m，若以3m ³ /s速度把水注入水槽，在水面高2m时，求水面上升的速度．

13．求下列各函数的微分．

① ②

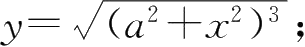
③ y = x sin x +cos x ；　　　④ y =arctane ^x ；

⑤ y =ln（1+ x ⁴ ）；　　　⑥ y =e ^{- x} -cos（3- x ）．

14．在括号内填入适当函数，使下列等式成立．

①d（　）=3d x ；　　　②d（　）=2 x d x ；

③d（　）=e ^x d x ；　　　④d（　）=sin t d t ；

⑤ 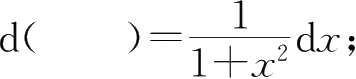⑥d（　）=sec ² x d x ．

15．已知 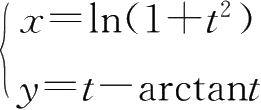，求

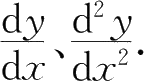
16．在| x |很小时，证明下列各近似公式．

①e ^{x ≈1+} x ；　　　②（1+ x ） ⁿ ≈1+ nx ；

③tan x ≈ x ；　　　④ln（1+ x ）≈ x ．

17．求下列各式的近似值．

①e ^1.01 ；　　　②

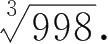
18．造一个半径为1m的球壳，厚度为1.5cm，需用材料多少立方米？

19．为计算球的体积准确到1%，度量球的半径时允许的相对误差是多少？

（B）

20．设 f （ x ）为可导函数， y = f （sin ² x ）+ f （cos ² x ），若令 u =cos x ，证明：

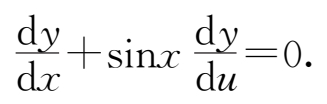
21．求由方程 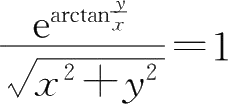所确定的隐函数 y = f （ x ）的导数．

22．求由参数方程 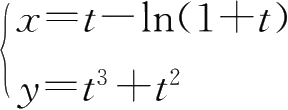所确定的函数的二阶导数 ．

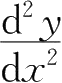23．求函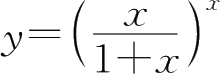数 的导数．

24．如果函数 y = f （ x ）在点 x = x ₀ 处当自变量有增量Δ x 时，函数有增量

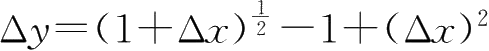
求函数在点 x ₀ 处的微分d y ． 2kT4WLrR0ZVq6PKbeg65mnWE7dmVNz3KW9ZfuVFFA+/Vt6V0bGVxJnSi1a7+RnJ8