




1.D 2.D 3.C 4.C 5.C 6.A 7.B 8.C 9.D 10.D 11.B 12.A 13.B 14.C 15.A 16.D 17.C 18.C 19.B 20.B
21.正确答案C
原式解出:
x
2
=
y
-1
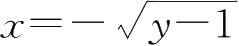 [
x
∈(-∞,0)]
[
x
∈(-∞,0)]
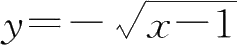
22.正确答案C
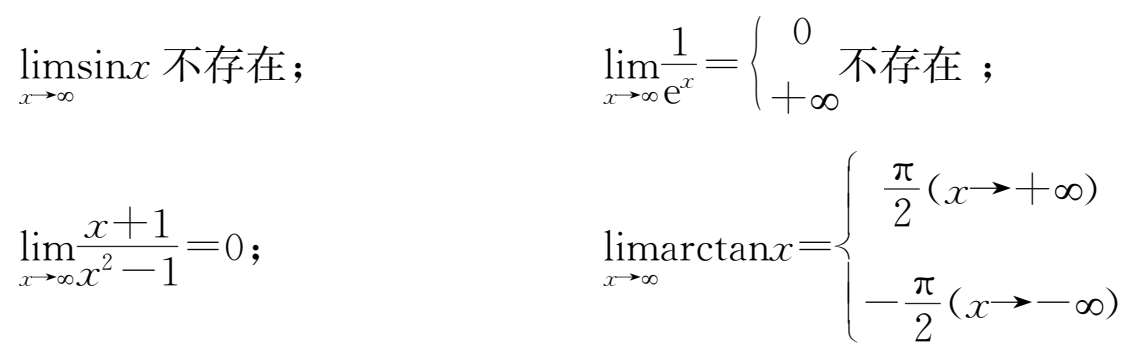
23.正确答案D
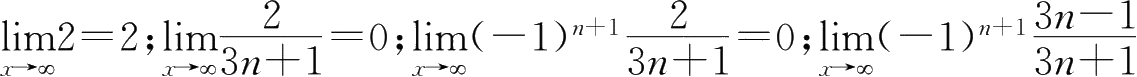 不存在.
不存在.
24.正确答案C
因为
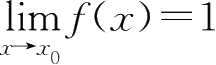 存在,所以左右极限都存在,A、B、D都是正确的.
存在,所以左右极限都存在,A、B、D都是正确的.
25.正确答案B
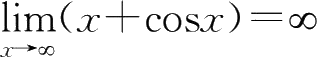
26.正确答案C
当 x =0, x =1时,函数无定义,所以不连续.
27.正确答案D
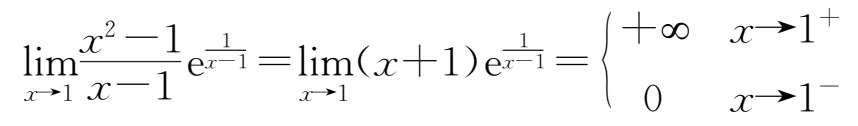
28.正确答案B
当|
x
|<1时,
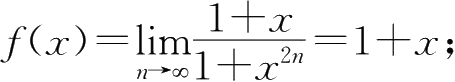
当|
x
|>1时,
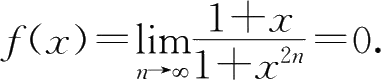 而
f
(-1)=0,
f
(1)=1.于是
而
f
(-1)=0,
f
(1)=1.于是
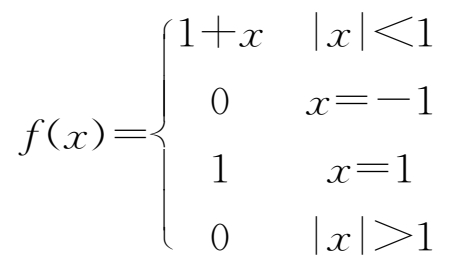
由于
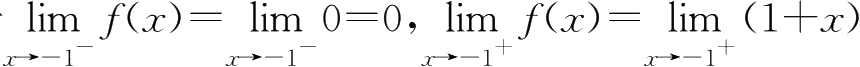 =0,
f
(-1)=0,
x
=-1连续
=0,
f
(-1)=0,
x
=-1连续
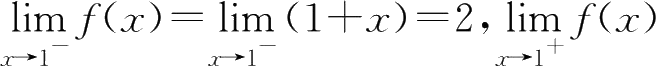 =0,
x
=1不连续.
=0,
x
=1不连续.
29.正确答案C
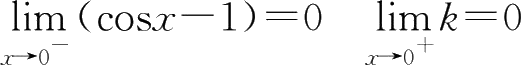
30.正确答案D
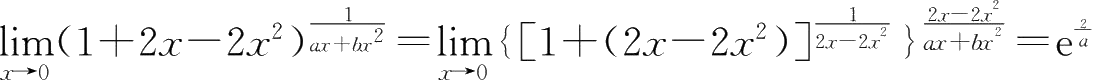 =2,
=2,
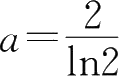 ,
b
为任意值.
,
b
为任意值.
1.
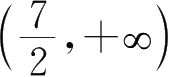 2.
2.
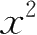 +4
x
+3 3.0 4.1 5.e
km
6.-1 7.高 8.0 9.0 10.1
+4
x
+3 3.0 4.1 5.e
km
6.-1 7.高 8.0 9.0 10.1
1.错 2.错 3.对 4.对 5.错 6.错 7.错 8.错 9.对 10.错
1.
①-1≤ x ≤1;② x > c / b ( b >0), x < c / b ( b <0).
2.
①定义域不同,故为不相同的函数;②定义域不同,故为不相同的函数;
③对应关系不同,为不相同的函数;④定义域不同,为不相同的函数.
3.
f (0.5)=2, f (-0.5)=1+(-0.5) 2 =1.25.
4.
(1)
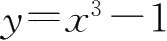 (2)
(2)
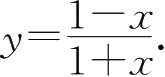
5.
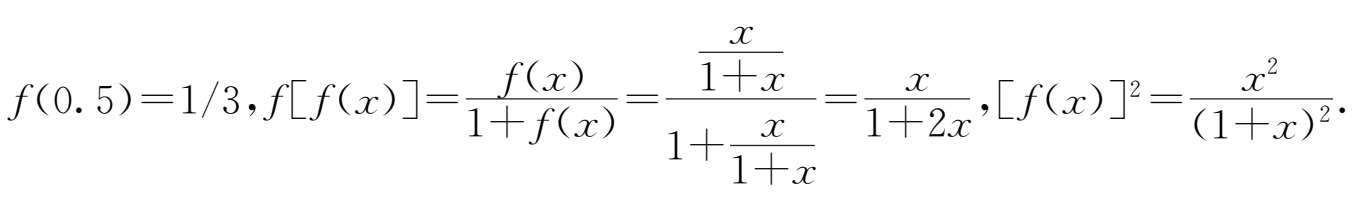
6.
由
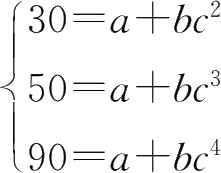 得
得
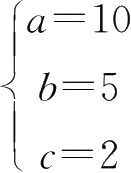
∴ Q = Q ( p )=10+5·2 p .
7.
①函数 y =arctan( x 2 )可分解为由 y =arctan u 和 u = x 2 复合而成;
②函数
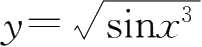 可分解为由
可分解为由
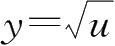 ,
u
=sin
v
及
v
=
x
3
复合而成;
,
u
=sin
v
及
v
=
x
3
复合而成;
③函数
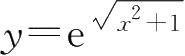 可分解为由
y
=e
u
,
可分解为由
y
=e
u
,
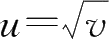 及
v
=
x
2
+1复合而成;
及
v
=
x
2
+1复合而成;
④函数 y =lnsin x 可分解为由 y =ln u 和 u =sin x 复合而成.
8.
①∵ f ( x )的定义域为 D =[0,1],
∴0≤ x 2 ≤1
∴ f ( x 2 )的定义域为[-1,1];
②∵0≤sin x ≤1,
∴ f (sin x )的定义域为[2 k π,2 k π+π], k ∈ Z ;
③∵0≤ x + a ≤1,∴ f ( x + a )的定义域为[- a ,1- a ];
④当
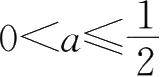 时,其的定义域为[
a
,1-
a
],
时,其的定义域为[
a
,1-
a
],
当
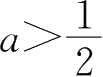 时,其的定义域为
Φ
.
时,其的定义域为
Φ
.
9.
(1)∵ g ( x )=e x ,
∴当 x <0, g ( x )=e x <1.∴ f [ g ( x )]=1,
当 x =0, g ( x )=e x =1∴ f [ g ( x )]=0,
当 x >0, g ( x )=e x >1∴ f [ g ( x )]=-1.
(2)当-1< x <1时, g [ f ( x )]=e,
当 x =±1时, g [ f ( x )]=1,
当 x >1或 x <-1时, g [ f ( x )]=e -1 .
(3)画图略.
10.
∵
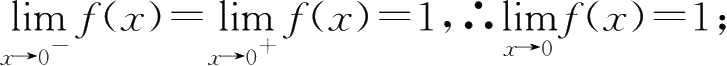
∵
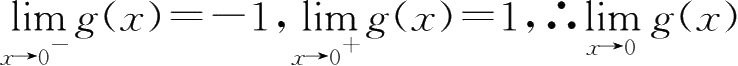 不存在.
不存在.
11.
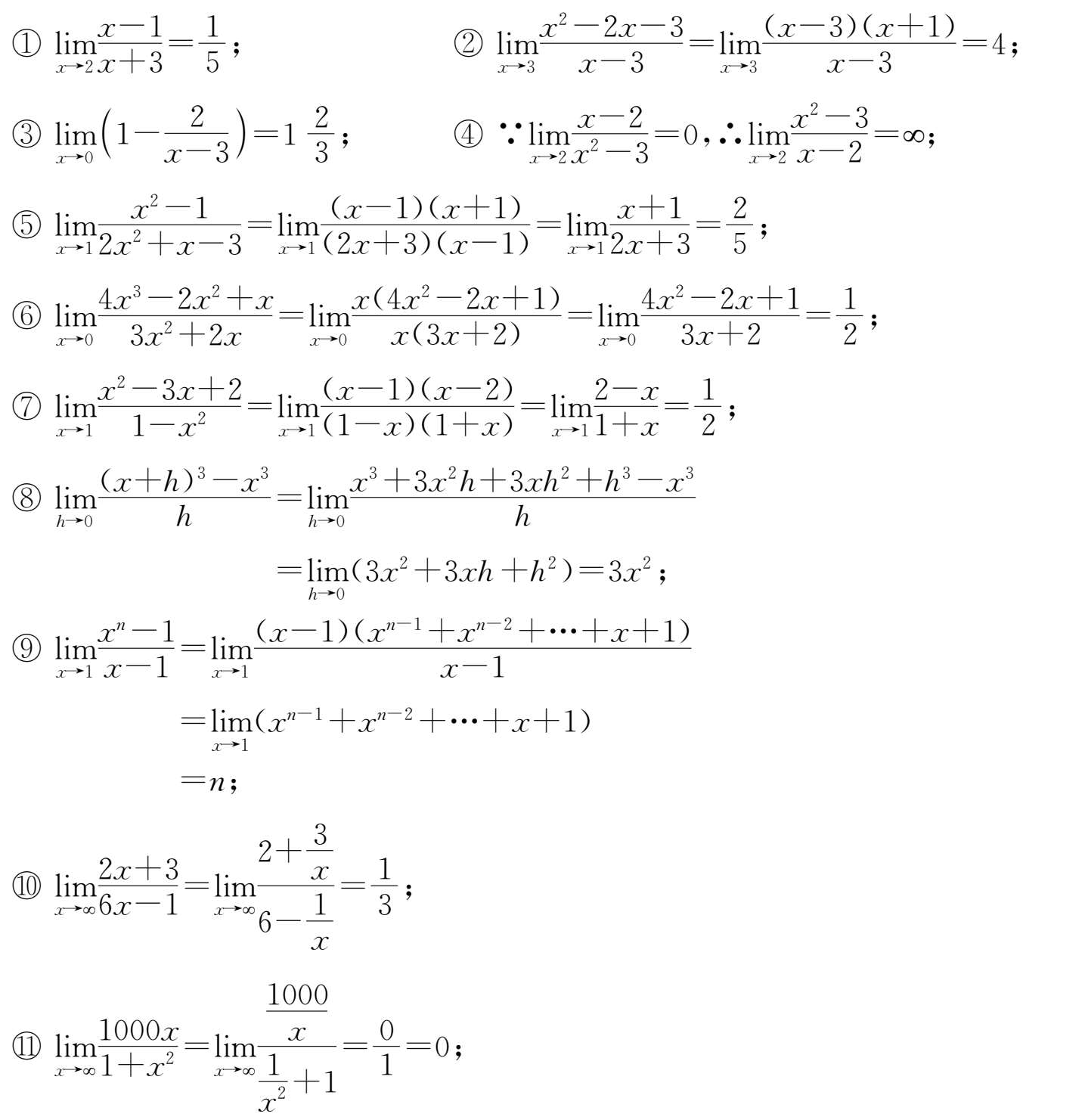

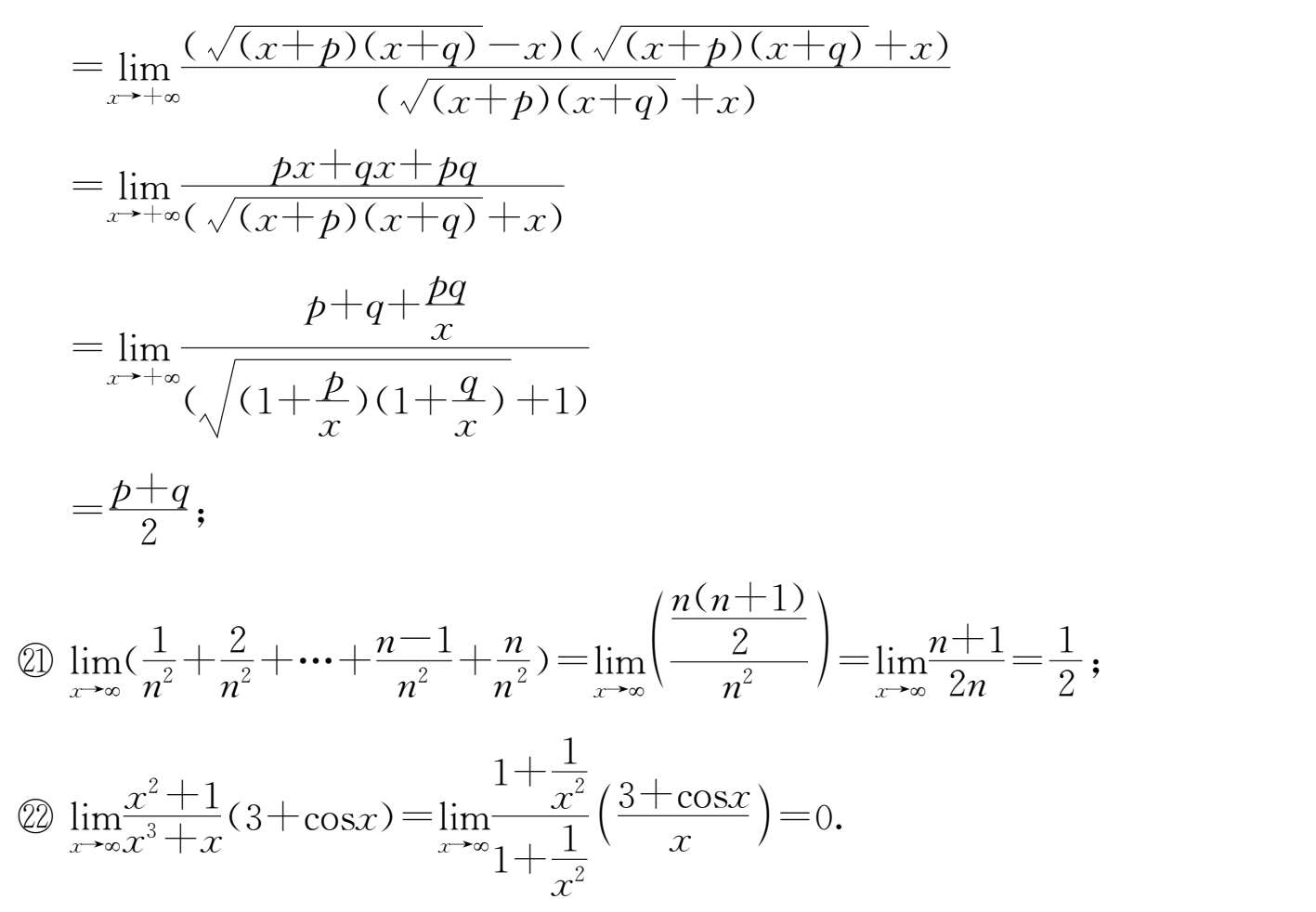
12.
①
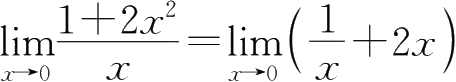 =∞,为无穷大;
=∞,为无穷大;
②
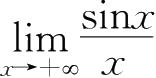 =0,为无穷小;
=0,为无穷小;
③
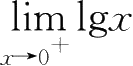 =-∞,为无穷大;
=-∞,为无穷大;
④
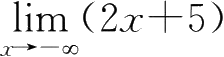 =-∞,为无穷大;
=-∞,为无穷大;
⑤
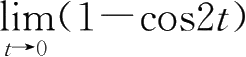 =0,为无穷小;
=0,为无穷小;
⑥
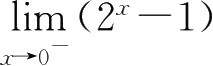 =0,为无穷小.
=0,为无穷小.
13.
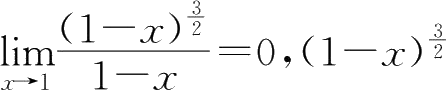 为1-
x
的高阶无穷小;
为1-
x
的高阶无穷小;
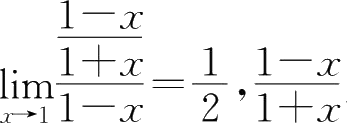 为1-
x
的同阶无穷小;
为1-
x
的同阶无穷小;
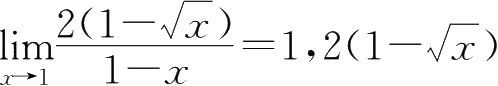 为1-
x
的等价无穷小.
为1-
x
的等价无穷小.
14.
由
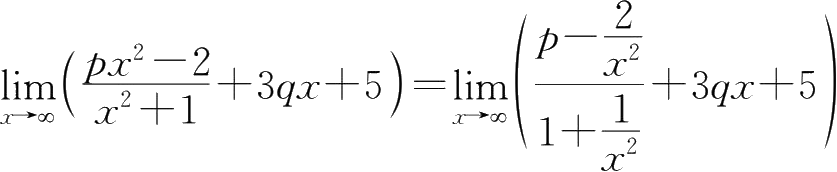
∴ p =-5, q =0时, y 为无穷小; q ≠0时, p 为任意常数, y 为无穷大.
15.
①
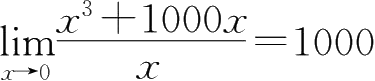 ,为同阶无穷小量;
,为同阶无穷小量;
②
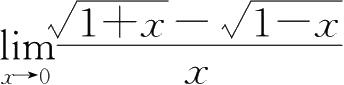 =1,为等价无穷小量;
=1,为等价无穷小量;
③
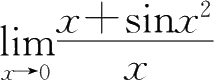 =1,为等价无穷小量;
=1,为等价无穷小量;
④
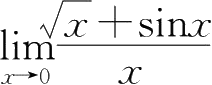 =∞,为较低阶无穷小量;
=∞,为较低阶无穷小量;
⑤
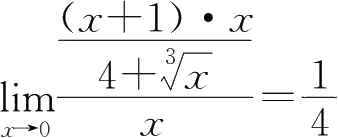 ,为同阶无穷小量;
,为同阶无穷小量;
⑥
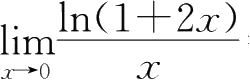 =2,为同阶无穷小量.
=2,为同阶无穷小量.
16.
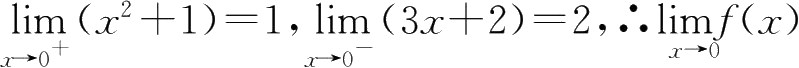 不存在;
不存在;
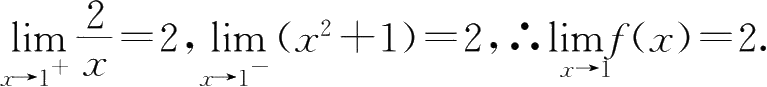
17.
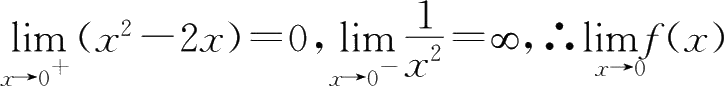 不存在;
不存在;
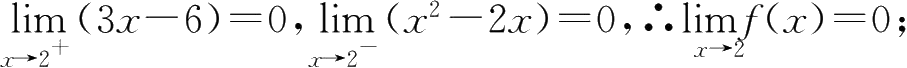
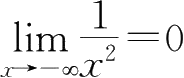 ;
;
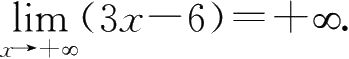
18.
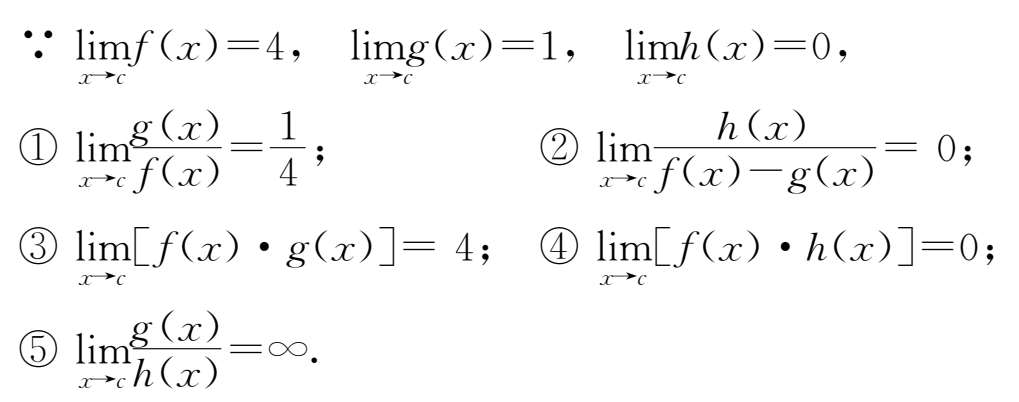
19.
由 x 2 -2 x + k =( x -3)( x +1)+(3+ k ),∴ k =-3.
20.
由 x 2 + ax + b =( x -1)( x + a +1)+( b + a +1)=0 b + a +1=0
而 x =1时 x + a +1=-5,∴ a =-7, b =6.
21.
由
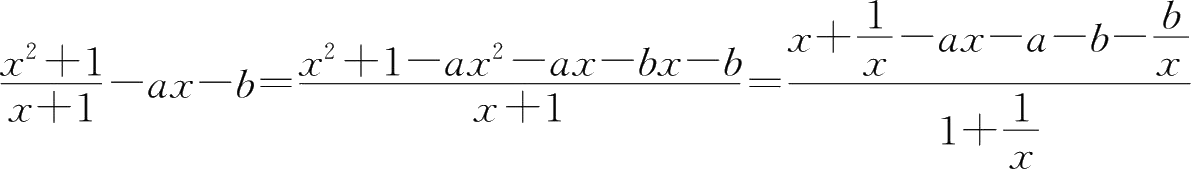
有 x - ax - a - b =0,即 x (1- a )-( a + b )=0
∴1- a =0, a + b =0.可解出 a =1, b =-1.
22.
①
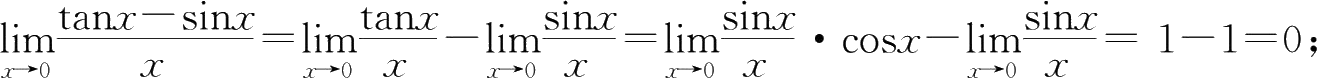
②
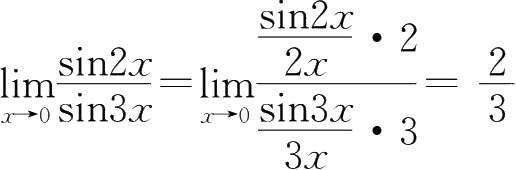 (
x
→0时有2
x
→0,3
x
→0);
(
x
→0时有2
x
→0,3
x
→0);
③
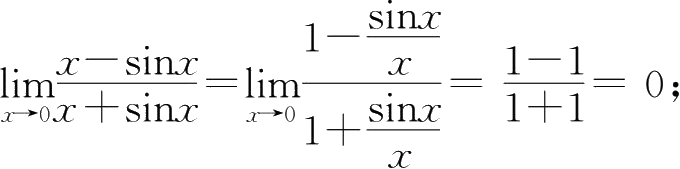
④设 y =arcsin x ,有 x →0时, y →0
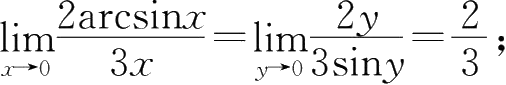
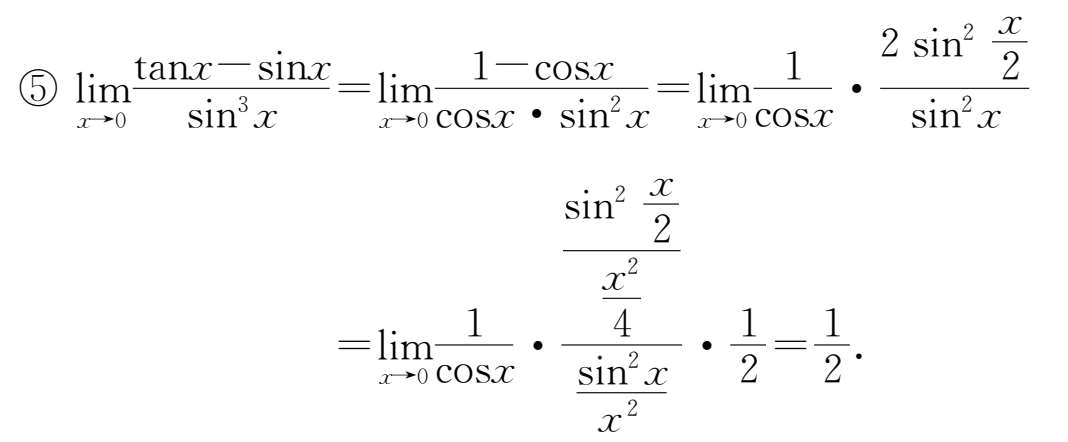
23.
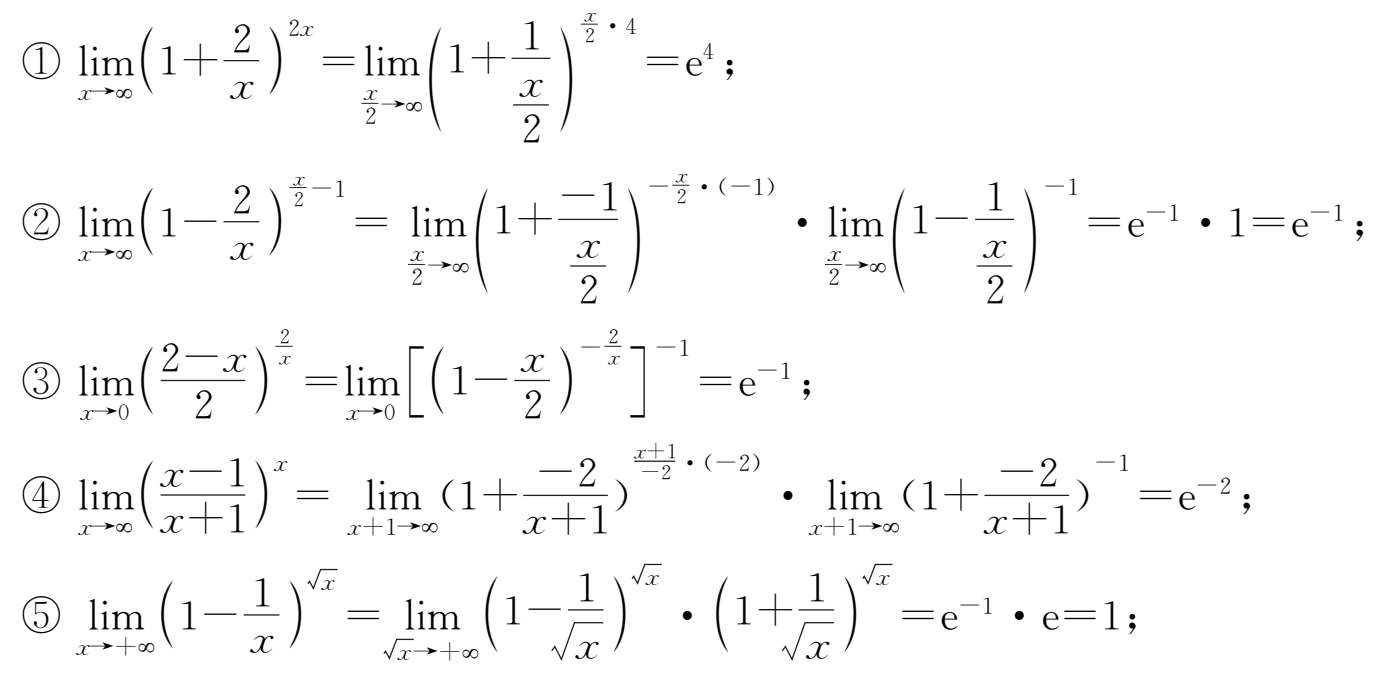
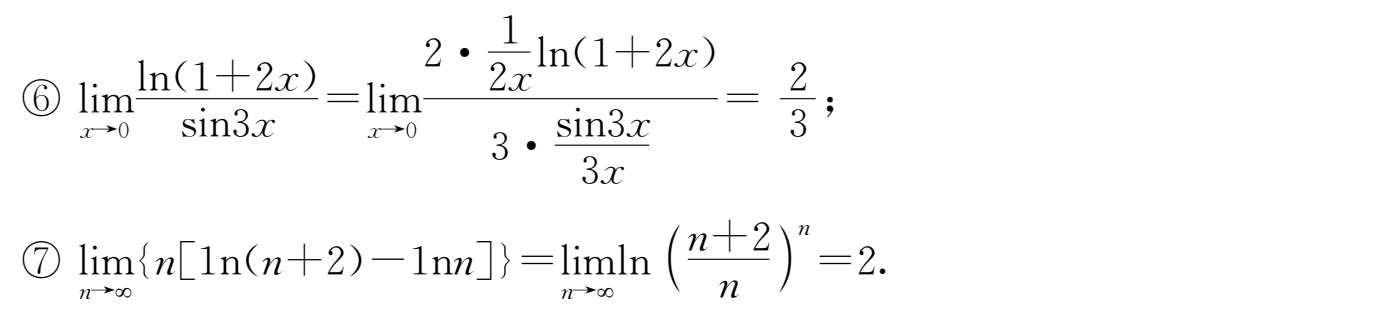
24.
①
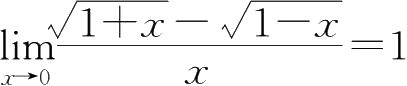 ,
f
(0)=1;②
,
f
(0)=1;②
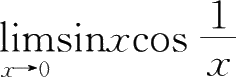 =0,
f
(0)=0;
=0,
f
(0)=0;
③由
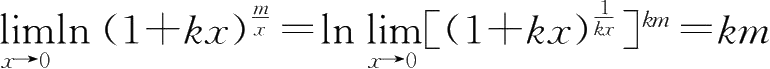 ,∴补充定义
f
(0)=
km
.
,∴补充定义
f
(0)=
km
.
25.根据连续函数性质,直接将数值代入.
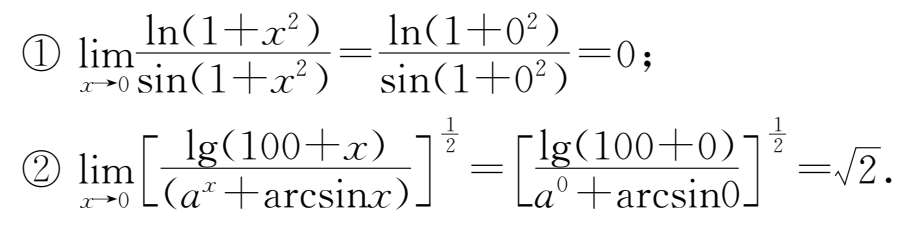
26.
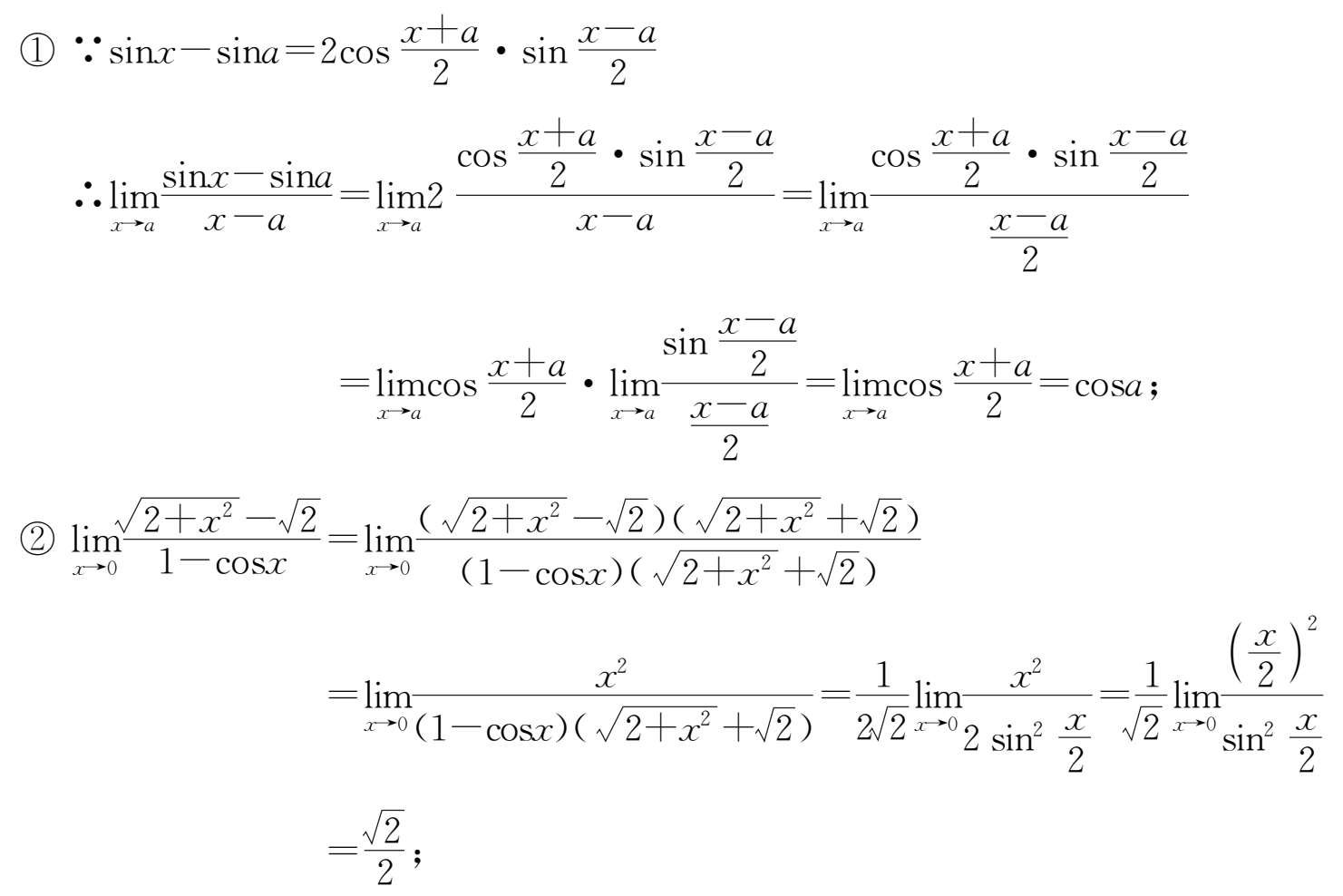
③令 x -1= t ,则 x =1+ t .当 x →1时, t →0,于是
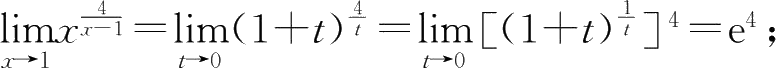
④
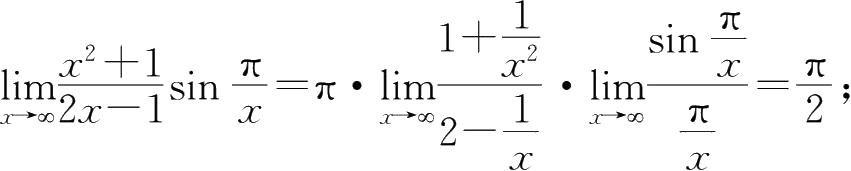
⑤因为
x
→0-时,
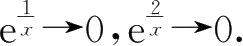
所以
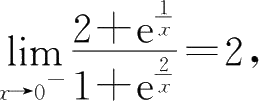
当
x
→0
+
时,
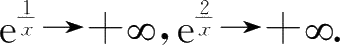
所以
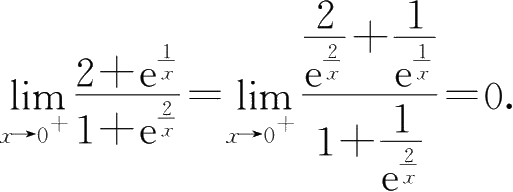
则左极限与右极限不相等,故
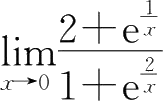 不存在.
不存在.
27.由于
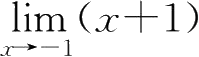 =0,极限
=0,极限
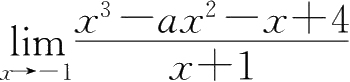 存在,
存在,
故必有
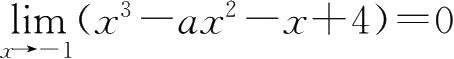 ,于是有4-
a
=0,即
a
=4.
,于是有4-
a
=0,即
a
=4.
将 a =4代回原极限式有:
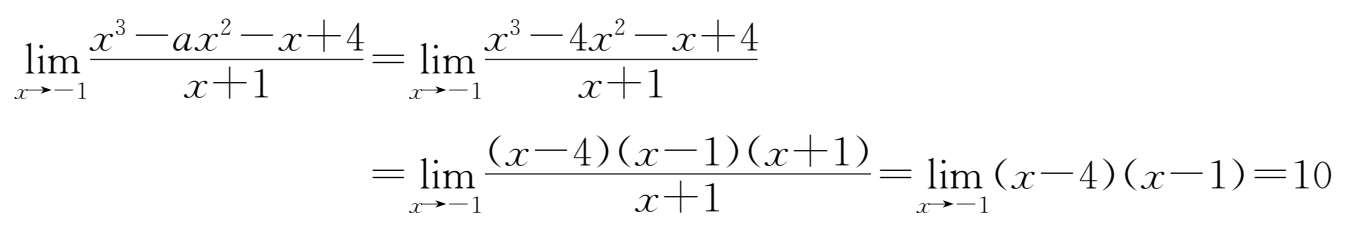
所以,所求 L =10, a =4.