




1.若函数 y = f ( x )在点 x 0 处导数 f' ( x )=0,则曲线在点( x 0 , f ( x 0 ))处的法线( ).
A.与 x 轴相平行
B.与 x 轴相垂直
C.与 y 轴相垂直
D.与 x 轴既不平行又不垂直
2.函数 y = x 3 在[-3,1]上的最小值是( ).
A.0
B.-1
C.-3
D.27
3. y = x 4 -2 x 3 在定义域内( ).
A.有两个极值点
B.有一个极值点
C.有三个极值点
D.无极值点
4.
 =( ).
=( ).
A.

B.-

C.2
D.-2
5.
 =( ).
=( ).
A.0
B.

C.
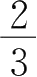
D.1
6.若在区间( a , b )内 f' ( x )<0, f'' ( x )>0,则函数 f ( x )在此区间内( ).
A.单调减,凹曲线
B.单调增,凹曲线
C.单调减,凸曲线
D.单调增,凸曲线
7.已知 f ( x )= x 3 + ax 2 + bx 在 x =1处取得极小值-2,则( ).
A. a =1, b =2
B. a =0, b =-3
C. a = b =2
D. a = b =1
8.下列极限中能使用罗必达法则的有( ).
A.
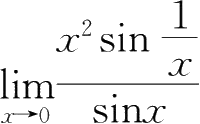
B.

C.

D.

9.
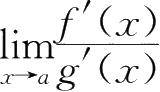 =
A
(或∞)是使用罗必达法则计算未定式
=
A
(或∞)是使用罗必达法则计算未定式
 的( ).
的( ).
A.必要条件
B.充分条件
C.充要条件
D.无关条件
10.函数 y = ax 2 + c 在区间(0,+∞)内单调增加,则 a , c 应满足( ).
A. a <0且 c =0
B. a >0且 c 是任意实数
C. a <0且 c ≠0
D. a <0且 c 是任意实数
11.函数
 满足拉格朗日中值定理的区间是( ).
满足拉格朗日中值定理的区间是( ).
A.[-2,2]
B.[1,2]
C.[-2,0]
D.[0,1]
12. f' ( x )=0是可导函数 y = f ( x )在 x = x 0 处取得极值的( ).
A.必要但不充分条件
B.充分但不必要条件
C.充要条件
D.既不充分也不必要条件
13.若函数 f ( x )与 g ( x )在区间( a , b )内每一点都有 f' ( x )= g' ( x ),则在区间( a , b )内必有( ).
A. f ( x )= g ( x )
B. f ( x )= Cg ( x )
C. f ( x )= C 1 , g ( x )= C 2
D. f ( x )= g ( x )+ C
(其中 C 为任意常数, C 1 、 C 2 为常数)
14.已知
f
(3)=2,
f'
(3)=-2,则
 =( ).
=( ).
A.-4
B.8
C.0
D.不存在
15.点 x =0是函数 y = x 4 的( ).
A.驻点但非极值点
B.拐点
C.驻点且是拐点
D.驻点且是极值点
16.函数 f ( x )在闭区间[ a , b ]上连续且单调减少,则 f ( x )在[ a , b ]上( ).
A.最大值为 f ( a )
B.最大值为 f ( b )
C.最大值为极大值
D.最大值不存在
17.设在[0,1]上 f'' ( x )>0,则 f' (0), f' (1), f (1)- f (0)或 f (0)- f (1)的大小顺序是( ).
A. f' (1)> f' (0)> f (1)- f (0)
B. f' (1)> f (1)- f (0)> f' (0)
C. f (1)- f (0)> f' (1)> f' (0)
D. f' (1)> f (0)- f (1)> f' (0)
18.函数 f ( x )的定义域为(0,+∞)且 f ( x )>0, f' ( x )>0, m 为正整数,则函数 y =( x + m ) f ( x + m )( ).
A.存在极大值
B.存在极小值
C.是增函数
D.是减函数
19.已知曲线 y = ax 3 + bx 2 的拐点为(1,3),则 a , b 的值为( ).
A.
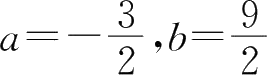
B.

C.
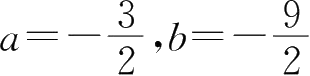
D.

20.
 =( ).
=( ).
A.-1
B.1
C.0
D.∞
21.设
 ,则
,则
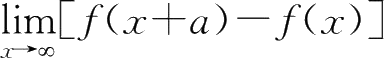 =( ).
=( ).
A. a
B.

C. ka
D.0
22.已知函数
f
(
x
)在[0,+∞)上连续,在(0,+∞)上可导,且
f'
(
x
)在(0,+∞)内单调增加,且
f
(0)=0,则函数
 在(0,+∞)内( ).
在(0,+∞)内( ).
A.单调增加
B.单调减小
C.先增加后减小
D.先减小后增加
23.方程 x e x = a ( a >0)有( )个实根.
A.0
B.1
C.2
D.3
24.
 =( ).
=( ).
A.1
B.-1
C.e -1
D.0
25.曲线 y = k ( x 2 -3) 2 的拐点处的法线通过原点,则 k 的值为( ).
A.

B.

C.
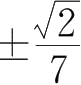
D.

26.设 f ( x ), g ( x )是恒大于零的可导函数,且 f' ( x ) g ( x )- f ( x ) g' ( x )<0,则当 a < x < b 时,( ).
A. f ( x ) g ( b )> f ( b ) g ( x )
B. f ( x ) g ( a )> f ( a ) g ( x )
C. f ( x ) g ( x )> f ( b ) g ( b )
D. f ( x ) g ( x )> f ( a ) g ( a )
27.已知函数
f
(
x
)=
a
sin
x
+
 在
在
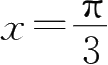 处取得极值,则
a
的值为( ),而且该极值是( ).
处取得极值,则
a
的值为( ),而且该极值是( ).
A.
a
=-2,极小值是-
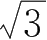
B.
a
=2,极大值是
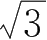
C.
a
=-2,极大值是-
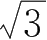
D.
a
=2,极小值是
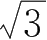
28.设
f
(
x
)有二阶连续导数,且
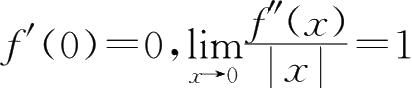 ,则( ).
,则( ).
A. f (0)是 f ( x )的极大值
B. f (0)是 f ( x )的极小值
C.(0, f (0))是曲线 y = f ( x )的拐点
D. f (0)不是极值,(0, f (0))也不是 y = f ( x )的拐点
29.曲线
 有( ).
有( ).
A.一条水平渐近线与一条垂直渐近线
B.一条垂直渐近线与一条斜渐近线
C.一条水平渐近线与一条斜渐近线
D.无渐近线
30.
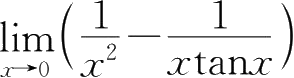 =( ).
=( ).
A.

B.

C.

D.
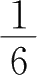
1.曲线上( )点,称作曲线的拐点.
2.
 =( ).
=( ).
3.
 =( ).
=( ).
4.
 =( ).
=( ).
5.
 =( ).
=( ).
6.函数 y =2 x 3 +14 x -7的单调增加区间为( ).
7.设
f
(
x
)=
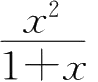 ,则
f
(
x
)在区间
,则
f
(
x
)在区间
 上的最大值为( ).
上的最大值为( ).
8.曲线
 有( )渐近线.
有( )渐近线.
9.曲线 f ( x )= x 3 -3 x 上的拐点为( ).
10.函数
 的渐近线为( ).
的渐近线为( ).
1.若
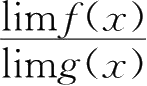 存在,则
存在,则
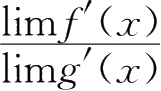 存在.( )
存在.( )
2.拉格朗日中值定律与柯西中值定律的几何意义相同.( )
3.罗尔中值定律是柯西中值定律的特殊情况.( )
4.驻点是可导函数极值点的充分条件.( )
5.若 x 0 是可导函数 f ( x )的一个极值点,则必有 f' ( x 0 )=0.( )
6.若函数在开区间内是单调的,则曲线必是凹的或必是凸的.( )
7.若 f'' ( x 0 )=0,则( x 0 , f ( x 0 ))必为曲线 y = f ( x )的拐点.( )
8.若 f ( x )在[0,+∞)上连续,且在(0,+∞)内 f' ( x )<0,则 f (0)为 f ( x )在区间上的最大值.( )
9. f'' ( x )=0是 y = f ( x )的图形在 x 0 处有拐点的充分条件.( )
10.曲线
 既有水平渐近线又有垂直渐近线.( )
既有水平渐近线又有垂直渐近线.( )
1.验证拉格朗日中值定理对函数 y =4 x 3 -5 x 2 + x -2在区间[0,1]上的正确性.2.在0< a < b 、 n >1时,证明 na n -1 ( b - a )< b n - a n < nb n -1 ( b - a ).
3.求下列极限.

4.验证
 存在,但不能用罗必达法则计算.
存在,但不能用罗必达法则计算.
5.求下列极限.

6.求下列各函数的单调区间.
① f ( x )= x 3 -3 x +2; ② y =( x -1)( x +1) 3 ;
③
y
=
 ④
y
=
x
-ln(
x
+1).
④
y
=
x
-ln(
x
+1).
7.求下列各函数的极值.
①
y
=
 ; ②
y
=
; ②
y
=
 ;
;
③ f ( x )=( x -1) 3 (2 x +3) 2 ; ④ y = x -ln( x 2 +1).
8.求下列各函数的最值.
① y =( x 2 -1) 3 +1,[-2,1]; ② y = x 5 -5 x 4 +5 x 3 +1,[-1,2];
③
y
=
 ,[-6,8]; ④
y
=3
x
,[-1,4].
,[-6,8]; ④
y
=3
x
,[-1,4].
9.肌肉或皮下注射后,血药浓度为
 ,其中
A
>0,0<
a
1
<
a
2
. 求血药浓度的最大值.
,其中
A
>0,0<
a
1
<
a
2
. 求血药浓度的最大值.
10.某厂有一个圆柱形油罐,直径6m、高2m,想用车高1.5m、吊臂长15m的汽车吊把油罐吊到6.5m高的柱子上去安装.试问能不能吊上去?
11.求曲线 y = x 3 -5 x 2 +3 x -5的凹凸区间和拐点.
12.做下列函数的图像.
① y =2 x 3 -3 x 2 ; ② y = x 4 -2 x 2 -5;
③
y
=
x
+
x
-1
; ④
y
=
 .
.
13.把下列函数展开为幂级数.
①
y
=
 ; ②
y
=sin(
x
+
a
).
; ②
y
=sin(
x
+
a
).
14.用幂级数展开式证明欧拉公式,即
e ix =cos x + i sin x .
15.证明:当
x
>0时,
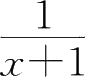 <ln(
x
+1)-
<ln(
x
+1)-
 .
.
16.证明:当
 时,arctan
x
-
时,arctan
x
-
 -ln2.
-ln2.
17.

18.

19.设曲线 y = x 3 +3 ax 2 +3 bx + c 在 x =-1处取得极大值,点(0,3)是拐点,求 a , b , c .
20.设
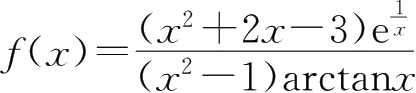 ,求渐近线.
,求渐近线.