




静力学基本公理是指人们在生产和生活实践中长期积累和总结出来并通过实践反复验证的具有一般规律的定理和定律。它是静力学的理论基础,且不用加以数学推导。
作用在同一刚体上的两个力,使刚体平衡的充分和必要条件是:这两个力大小相等、方向相反且作用在同一直线上。
应当指出,二力平衡原理对刚体是必要且充分的,对变形体则是必要的,而不是充分的。
利用此原理可以确定力的作用线位置,例如刚体在两个力作用下平衡,若已知两个力的作用点,那么这两个作用点的连线即为力的作用线。
实际工程中把只受两个力作用而平衡的构件称为二力构件,若其为直杆,则称为二力杆。
在作用于刚体上的力系中,加上或去掉任意一个平衡力系,则不会改变原力系对刚体的作用效果。此公理表明平衡力系对刚体不产生运动效应,其适用条件只是刚体。加减平衡力系公理是力系简化的重要依据。
由上述两个公理尚可导出一个推论。
推论:力的可传性原理。
作用于刚体上的力可沿其作用线移动到刚体内任意一点,而不改变它对刚体的作用效应。
证明:如图1-3所示,设 F 作用在 A 点,在其作用线另一点 B 点上加上一对沿作用线的二力平衡力 F 1 和 F 2 且有 F 1 =- F 2 = F ,则 F 、 F 1 和 F 2 构成新的力系,由加减平衡力系原理减去 F 和 F 2 构成二力平衡力,从而将 F 移动作用线的另一点 B 上。
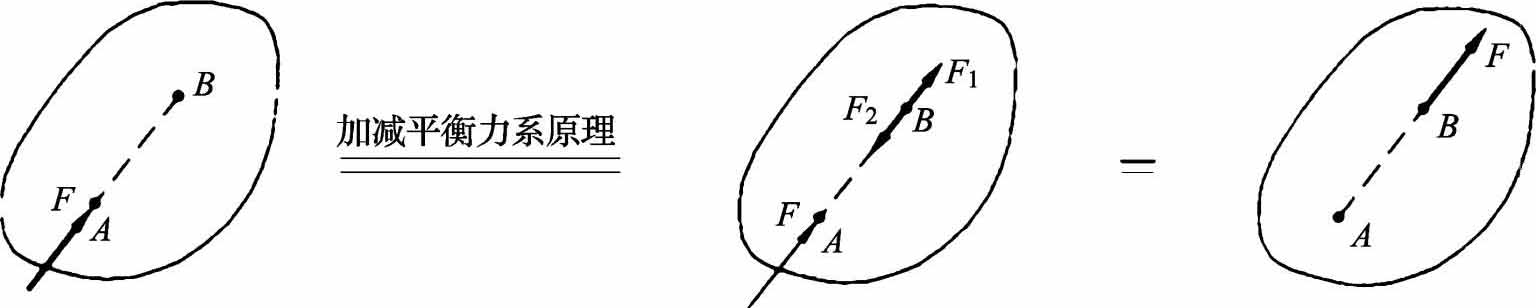
图1-3 力的可传性
该推论表明,对于刚体来说,力的作用点在力的作用线上的位置不是决定其作用效应的要素,所以,力的三要素是力的大小、方向和作用线。
作用于物体上同一点的两个力可以合成为作用于该点的一个合力,其大小和方向由这两个力为邻边所构成的平行四边形的对角线来确定,如图1-4所示。 R 为 F 1 和 F 2 的合力,即合力等于两个分力的矢量和,其表达式为:

由上述公理又可导出下列推论。
推论:三力平衡汇交定理。
刚体在三个力的作用下平衡,若其中两个力的作用线交于一点,则第三个力的作用线必通过该汇交点,且三力共面。
证明:如图1-5所示,设刚体在三个力 F 1 、 F 2 和 F 3 作用下处于平衡,若 F 1 和 F 2 汇交于 O 点,将此二力沿其作用线移动到汇交点 O 处,并将其合成 F 12 ,则 F 12 和 F 3 构成二力平衡力,所以 F 3 必通过汇交点 O ,且三力必共面。
应当指出,三力平衡汇交定理的条件是必要条件,不是充分条件。同时它也是确定力的作用线的方法之一,即若刚体在三个力作用下处于平衡,若已知其中两个力的作用线汇交于一点,则第三个力的作用点与该汇交点的连线即为第三个力的作用线,其指向再由二力平衡公理来确定。
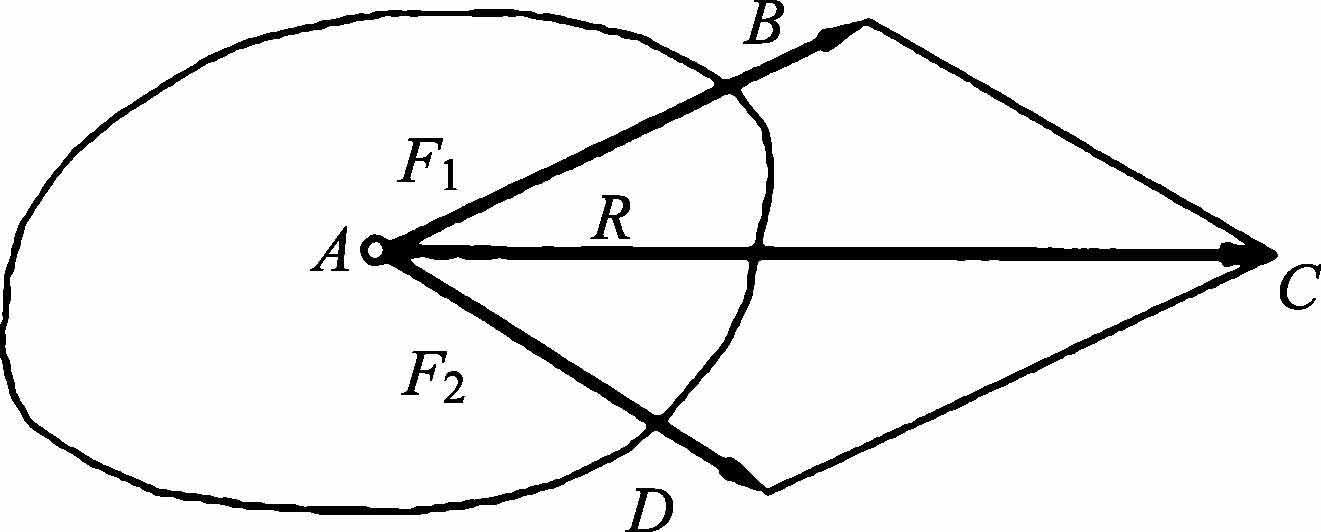
图1-4 力的平行四边形法则
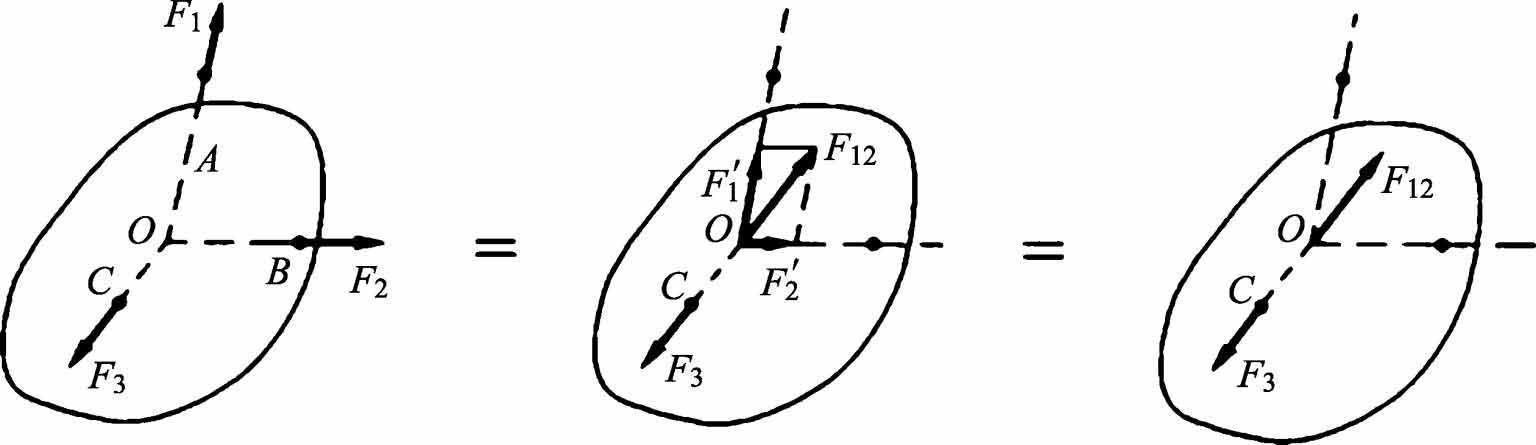
图1-5 三力平衡汇交定理
作用力和反作用力大小相等,方向相反,沿同一直线并分别作用在两个相互作用的物体上。
应当注意,作用力与反作用力与二力平衡力的区别,前者作用于两个不同的物体上,后者作用于同一个物体上。