




一般情况下,系统是由若干个客体组成,相互之间具有联系和依赖性,并具有特定功能。它可以是自然科学中的一些物质,例如,人体和钟表,也可以是各种组织,如学校。经济系统的本质是非线性的,对于经济系统的传统研究大多假设它是线性的。之所以这样做,是因为线性系统简单且较容易分析。现实中的经济系统却大多是非线性的,用线性分析范式来分析非线性系统的问题,会使分析结果与现实不符。采用非线性分析范式来分析非线性系统的问题能够真实地揭示经济系统的运行规律,可以更辩证地反映事物的本质,近年来成为解释和分析经济行为的主要工具。
系统是指由一些相互联系或相互依赖的若干客体组成的集合,具有特定功能的有机整体。系统可以是自然科学中的一些物质,也可以是各种社会事物或者组织。经济系统的本质是非线性的,而经济系统的传统研究大多假设其是线性的。之所以这样做,是因为线性系统简单且较容易分析。现实中的经济系统大多是非线性的,采用线性的分析范式会导致分析结果的误差随着时间的演化变得越来越大。非线性动力学理论则可以部分避免线性范式的弊端,应用非线性理论研究经济系统,可以更辩证地反映事物的本质,近年来成为解释和分析经济行为的主要工具。
动力系统(Dynamical System)是一个数学概念。物种繁衍、流体运动、经济系统的发展演变等都是随时间而演变,这些系统如果用一个数学模型来描述的话,可以表达为: φ t : X → X ,其中, X 是所有客体的各种状态构成的集合, φ t 表示 X 与时间 t 相关的动态变化规律。所以,动力系统可以描述几何空间中的一个点在遵循固定运行规则下,随时间变化的系统,如流体运动、物种绵续、钟摆晃动,宏观经济系统中的周期变换等数学模型都是动力系统。动力系统在运行过程中的状态是一系列被确定下来的实数,称为运行状态,运行状态的变动对应这组实数的变动。动力系统遵循一组固定的演化规则,这种规则是确定的。在给定的时间间隔内,系统沿演化规则从当前状态演化出一个未来的状态。
首先给出不动点的定义:
若 x ∗ 满足 F ( x ∗ )=0,则称 x ∗ 为不动点( Fixed Point )。从不动点出发的解的速度为零,因此它会停留在该点而且对所有的 t 都有 φ ( t : x ∗ )= x ∗ 。传统上也称不动点为平衡点(Equilibrium Point)。稳定性一词最早是从力学方面演化过来的,是指系统的量不随时间变化的平衡状态。在外力的干扰下,一定周期内物体能回到原来的位置,这个状态是“稳定的”;反之,一定周期内物体不能回到原来的位置,这个状态是“不稳定的”。这说明当力达到平衡时,物体就不再移动。在供应链系统,稳定性是指供应链中各企业主体的博弈结果达到最优状态。
供应链系统表现出复杂的非线性特征,非线性的供应链系统可能存在多个平衡点。这些平衡点中,有局部平衡点,也有整体平衡点。如果用线性范式分析供应链系统,那么它的平衡点是唯一的,这样会掩盖供应链的某些平衡点。
分岔(Bifurcation)的研究始于18世纪力学对于非线性振动失稳的研究。分岔问题与系统的稳定性问题相对但又密不可分。系统运行经过某个关键值时,相空间的拓扑结构会突然发生变化,改变原来运行的方向;也可以说,系统的拓扑结构发生了“质”的变化。例如,考虑一个系统如2-1所示:

x ∈ U ⊆ R n 为状态参数, μ =[ μ 1 , μ 2 ,…, μ m ] T ∈ J ⊆ R m 为分岔参数。当 μ 不断变化时,系统在向空间定态结构 μ 0 ∈ J 发生突然变化,解的数目发生了变化,则称系统在点 μ = μ 0 处发生分岔现象, μ 0 为系统的分岔的一个临界点。
分岔的类型主要有霍夫分岔(Hopf Bifurcation)、叉型分岔(Flip Bifurcation)和鞍-结分岔(Neimark-Sacker Bifurcation)。
一个耗散系统中解的情况可以用吸引子来定性说明。混沌的一个重要特征是奇异吸引子理论和分维。
假设系统的运动由 n 个一阶微分方程表示:
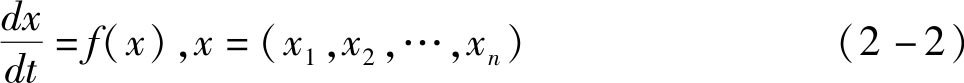
以 x 1 , x 2 ,…, x n 为坐标,系统运动的一个相空间。相空间内的每个点表示系统的解,它描述系统的运动状态,解的运动则称为相空间中的流。
Lanford对吸引子的定义为:相空间的一个子集 A 。
(1)
A
对于
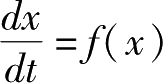 ,
x
=(
x
1
,
x
2
,…,
x
n
)产生的流是不变的;
,
x
=(
x
1
,
x
2
,…,
x
n
)产生的流是不变的;
(2) A 具有吸引性,存在一个 A 的邻域,该邻域内的流收缩至 A ;
(3)在 A 上的流是循环的;
(4) A 具有不可分割性,即不能把它划分为更小的集合。如果对它进行分割,就不能满足定义要求。简单说,吸引子就是一个动力系统经过长时间演化后的一个极限状态。
只有耗散的动力系统才具有吸引子,稳定、周期、拟周期和奇异吸引子为常见的几种吸引子形式。前面三种吸引子描述经典动力系统的规则有序运动,奇异吸引子表征耗散动力系统的混沌运动,它具有分维数的特征。图2-1就是著名的奇异吸引子——洛伦兹吸引子。
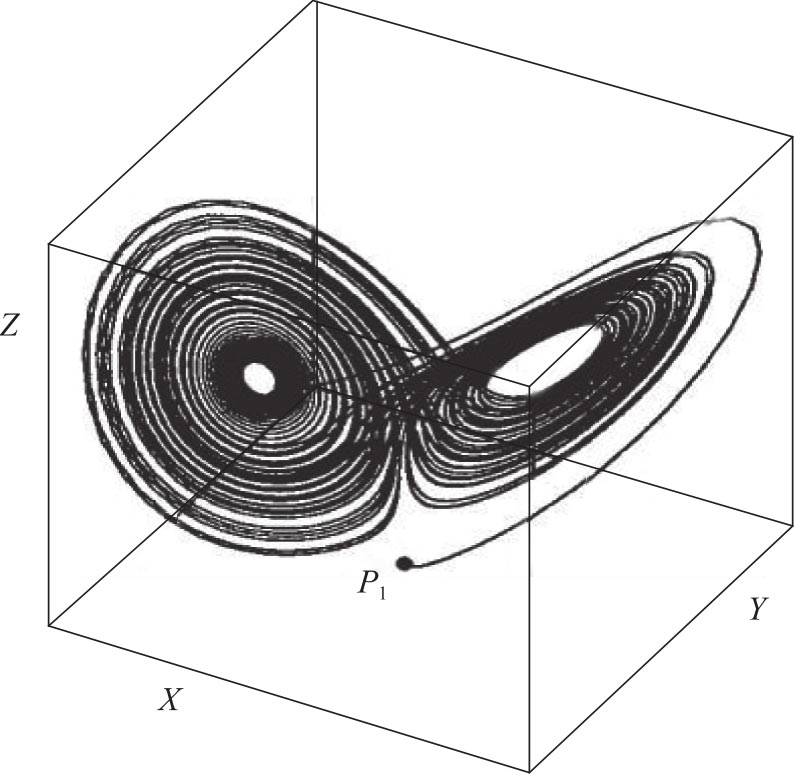
图2-1 洛仑兹吸引子
正的李雅普诺夫指数(Lyapunov Exponent)是混沌系统具有的一个重要特征。当动力系统的初值非常接近,随着时间的推移,它所产生的运动轨迹按指数分离。这说明动力系统运动轨道具有不稳定性,同时李雅普诺夫指数也可以用来刻画奇异吸引子性质。
下面用一维映射的例子来给李雅普诺夫指数下定义。

μ 为状态参数,设 x 0 , y 0 是一维相空间中相邻的两个点,于是
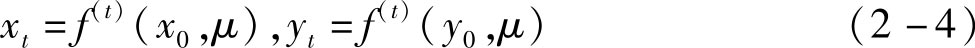
如果两个点之间的距离随时间呈指数变化,即
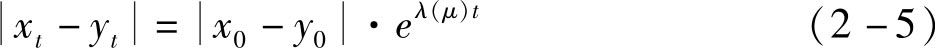
则
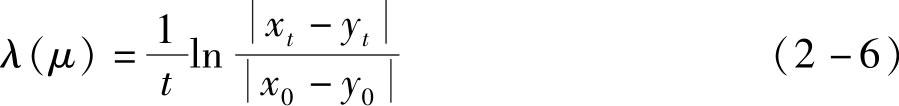
其中,当|
x
0
-
y
0
|→0,
t
→∞时,称
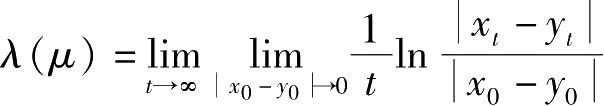 是一个动力系统的李雅普诺夫指数。当
λ
(
μ
)<0时,动力系统呈现出收敛的趋势;当
λ
(
μ
)>0时,动力系统呈现出发散的趋势;当多数
λ
(
μ
)>0,动力系统呈现出混沌状态。因此,李雅普诺夫指数反映了动力系统初始运动的细小差距,随着时间不断变化呈现出收敛或者发散的趋势。
是一个动力系统的李雅普诺夫指数。当
λ
(
μ
)<0时,动力系统呈现出收敛的趋势;当
λ
(
μ
)>0时,动力系统呈现出发散的趋势;当多数
λ
(
μ
)>0,动力系统呈现出混沌状态。因此,李雅普诺夫指数反映了动力系统初始运动的细小差距,随着时间不断变化呈现出收敛或者发散的趋势。
由此,可以推导出 n 维映射的李雅普诺夫指数。通过计算一个非线性系统的李雅普诺夫指数,可以判断这个系统是否出现混沌现象。
对混沌的研究还处于发展阶段,不同系统的各种复杂混沌特性尚未完全展示。目前,对混沌的定义影响比较大的是Li-Yorke以及Devaney。
李天岩—约克的混沌定义:连续自映射 f 在[ a , b ]上若满足以下条件,则系统就是混沌的。
(1) f 具有无上界的周期点;
(2)存在不可数子集合 S ⊂[ a , b ], S 满足以下 a 、 b 、 c 三个条件且其中无周期点:
a. 对任意
x
,
y
∈
S
,有
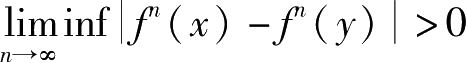 ;
;
b. 对任意
x
,
y
∈
S
,
x
≠
y
,有
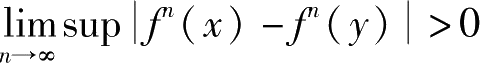 ;
;
c. 对任意
x
∈
S
和
f
的任意周期点
y
,有
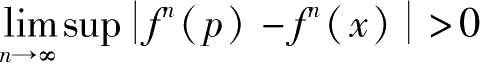 。
。
在李天岩—约克的混沌定义中,约束条件 a 和 b 表明对于任意属于 S 的点 x 、点 y 没有要求。约束条件 c 表明,点 x 、点 y 不会趋向任意的周期点。一个系统如果混沌,那么它一定存有无数个稳定的周期轨道和非周期轨道。Li-Yorke根据这一发现,提出了著名的“周期三意味着混沌”的理论。
1989年,Robert L. Devaney发现按照Li-Yorke的混沌定义可能导致混沌是不可观测的,后来他给出了混沌的另一个定义:若度量空间 V 上的映射满足以下三个条件,则称映射 f : V → V 是混沌的。
(1)对初始值的敏感依赖性。∃ δ >0,在 x 的 ε 邻域 I 内存在 y 和自然数 n ,使得 d ( f n ( x ), f n ( y ))> δ ,其中 ε >0, x ∈ V ;
(2)拓扑传递性。对
V
上的任意开集
X
,
Y
,存在
k
>0,
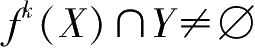 ;
;
(3) f 的周期点集在 V 中稠密。
Devaney定义中的第一个条件表明,混沌系统是不可预测的。因为混沌系统对初值很敏感并且具有强依赖性,初值不可能完全相同,所以混沌系统没有预测的机制。第二个条件表明,系统不能被分解为两个不变的开子集合。第三个条件表明在混沌中的有序,混沌态中还具有稠密的周期轨道。后来数学家们深入研究了Devaney定义中三个条件的内在联系,证明以下三点:
(1)拓扑传递性和稠密的周期轨道蕴含了系统对初值的敏感性;
(2)特定条件下,Devaney定义强于Li-Yorke定义;
(3)三个条件中的前两个条件可以作为因,第三个条件作为果。
混沌是一种复杂运动状态,存在于确定性的非线性系统。它具有内在随机性、有界性、遍历性、初值敏感性、分形和正的最大李雅普诺夫指数等特征。
(1)内在的随机性。虽然从内部来看混沌运动是杂乱无章的,但是在随机性中存在确定性一面。确定性系统的输入会产生确定性输出。但是在一个确定性的输入环境中也会产生类似随机的行为,表现出混沌特征。这说明混沌的随机性源于内在,与外部变量无关,因此称之为内在随机性。
(2)混沌的有界性和遍历性。系统处于混沌状态时,系统的运行轨线始终被吸引在一定范围内。整体上讲,混沌系统是有界并且稳定的;而遍历性则表现为其轨迹在有限时间内,会经历混沌吸引子内每一个点。
(3)对初值的敏感依赖性。不管离散或是连续,低维或是高维的混沌系统,其混沌运动都有一个基本的特征:系统的运动轨迹对于初始值的高度敏感。在混沌系统中,初始条件发生微小的变化,随着时间的不断变化,可能导致结果完全不同。这种对初始条件的敏感性,反映了动力系统内具有强烈的内在随机性,同时这种性质导致不能预测系统长期运动后的行为。
(4)与分形联系紧密。分形是几何学概念,表示那些无法用规则的几何语言叙述的复杂图形。混沌系统的初值或者参数的边界通常情况下是分形的,系统奇怪吸引子的截面往往也是分形的。
(5)与Lyapunov指数相关联。根据最大Lyapunov指数的大小可以对系统状态进行直观判断。系统的最大Lyapunov指数大于0,意味着在不论系统初始轨线相差多小,随系统演化其差距都会呈指指数增长,最后系统进入混沌状态。此特性在后续章节中被用来判断系统的状态。
除以上几个特性之外,混沌系统还具有标度性、奇怪吸引子、连续功率谱和分形等特性。
大量的研究证实,对于不同类型的确定性的耗散系统,在不同条件下会以不同的道路通向混沌,如倍周期分岔道路、茹厄勒-塔根司(Ruelle-Takens)道路、阵发性道路和Hopf分岔等。
(1)倍周期分岔道路
从字面意义上来看,倍周期分岔就是系统的运行轨迹出现2,4,8倍的变化。系统参数值的不断变化,会引起系统的拓扑结构发生质的变化。首先系统的运行轨迹进行第一次分岔,系统出现两条运行轨迹,之后,每条运行轨迹再一分为二。倍周期分岔的演化过程就是系统不断沿每条轨迹继续分裂最终演化为混沌。本书讨论的风险规避型供应链系统在一定条件下均通过被周期分岔进入混沌状态,具体的演化过程通过以下章节进行展示。下面通过例子详细说明倍周期分岔的演化过程。
考虑离散Logistic模型:

其中, μ 是正实数, x n ∈[0,1]代表某一物种在第 n 年所占的比例。
根据公式
x
n
+1
=
x
n
,得到两个平衡点
 ,
,
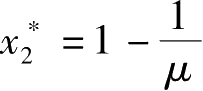 。
。
根据稳定性要求
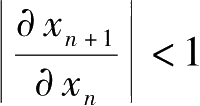 ,令
,令
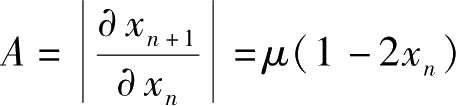 。
。
1)当0≤ μ ≤1
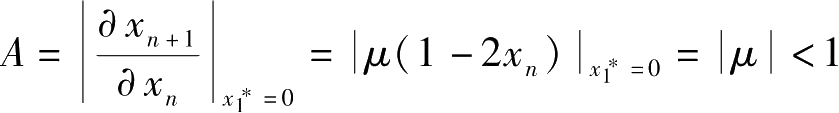 ,则平衡点
,则平衡点
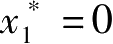 稳定。
稳定。
平衡点
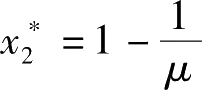 无实际意义,故
无实际意义,故
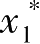 是系统唯一的不动点。
是系统唯一的不动点。
2)当1< μ ≤3
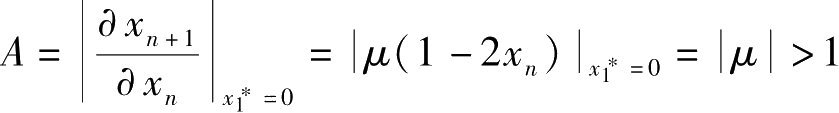 ,则
,则
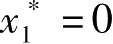 为系统的不稳定的不动点。
为系统的不稳定的不动点。
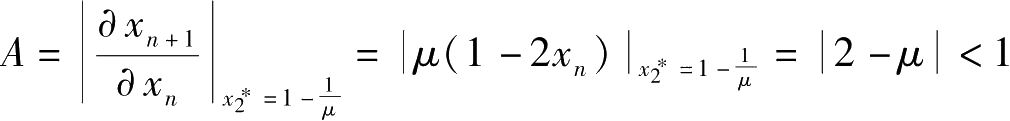 ,所以
,所以
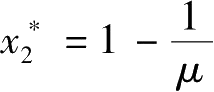 是映射在[0,1]内的稳定不动点。
是映射在[0,1]内的稳定不动点。
3)当
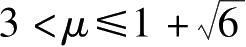
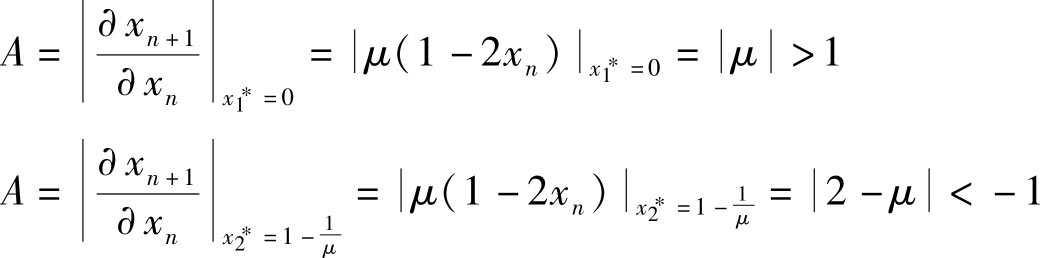
所以,离散Logistic系统的两个平衡点均失稳。
4)当 μ ≥3.5699
离散Logistic系统的平衡点均不满足稳定性条件。随着参数 μ 的变化系统的演化如图2-2所示。
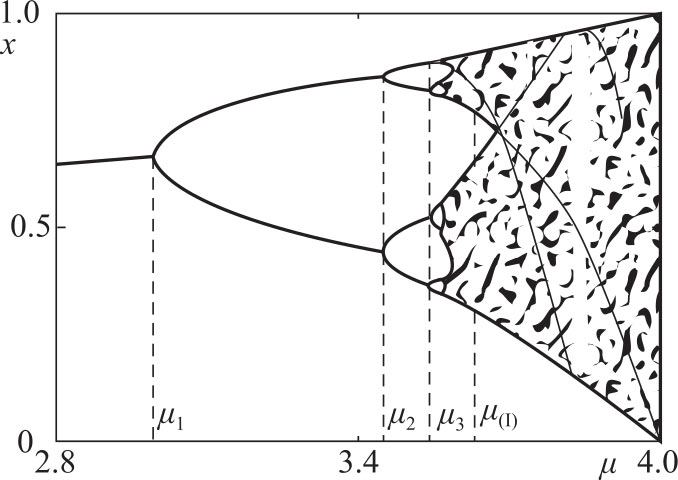
图2-2 Logistic模型演化过程
除Logestic系统,Duffing系统也是通过倍周期分岔通向混沌。Feigenbaum正是针对Logestic系统进行开创性研究,发现并确定两个普适常数。
(2)茹厄勒-塔根司(准周期)道路
菇厄勒(D. Ruelle,1971)和塔根斯(F. Takens,1978),法国著名科学家,提出准周期也是通向混沌的一条道路。因此,准周期道路又称茹厄勒-塔根斯道路。当流体系统发生湍流时,系统内不同频率的振荡互相耦合时,系统就会产生一系列新的耦合频率的振荡,从而导致混沌。其混沌过程为:随着参数的变化,系统由平衡点到极限环,然后极限环分岔为二维环面,继而再次分岔到三维环面进入混沌。菇厄勒和塔根斯分别用实验证明,在三次分岔后规则运动变得极度不稳定从而进入混沌。他们认为二维环面上的准周期运动,可能会直接失去稳定到达混沌。
(3)阵发性通向混沌(Pomeau-Manneville道路)
Pomeau和Manneville于1980年提出阵发性通向混沌道路。它在通向混沌道路上系统会出现规则行为不规则行为的随机交替现象。
(4)Hopf分岔通向混沌(Ruelle-Takens-Newhouse道路)
它是反映非线性耦合系统所造成的节律变化。一般情况下,一种规则的运动状态最多经过3次Hopf分岔就能够演化为混沌运动状态。
系统可以分为连续系统和离散系统,下面各章节中所讨论的风险规避型供应链的博弈决策都是发生在离散时间周期内。离散系统稳定性的判定需要借助一定的方法。为了得到离散系统的稳定性判据,先介绍连续系统的稳定性判据。
对于复杂的连续系统,它的运行轨迹发生在连续的时间内,可以运用连续系统的劳斯稳定性判据。下面通过构造Lyapunov函数来对连续系统的稳定性进行判断。
特征方程的特征值都为负实部时,连续系统处于稳定状态。但是,对于复杂的系统(阶次超过3次),很难求出系统的特征值。基于这样一种需求产生了劳斯(Routh)稳定判据。
假设系统的特征方程式为
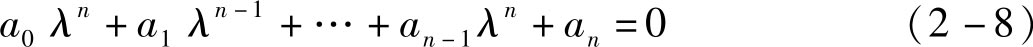
其中, a 0 >0,作Routh-Hurwitz行列式:
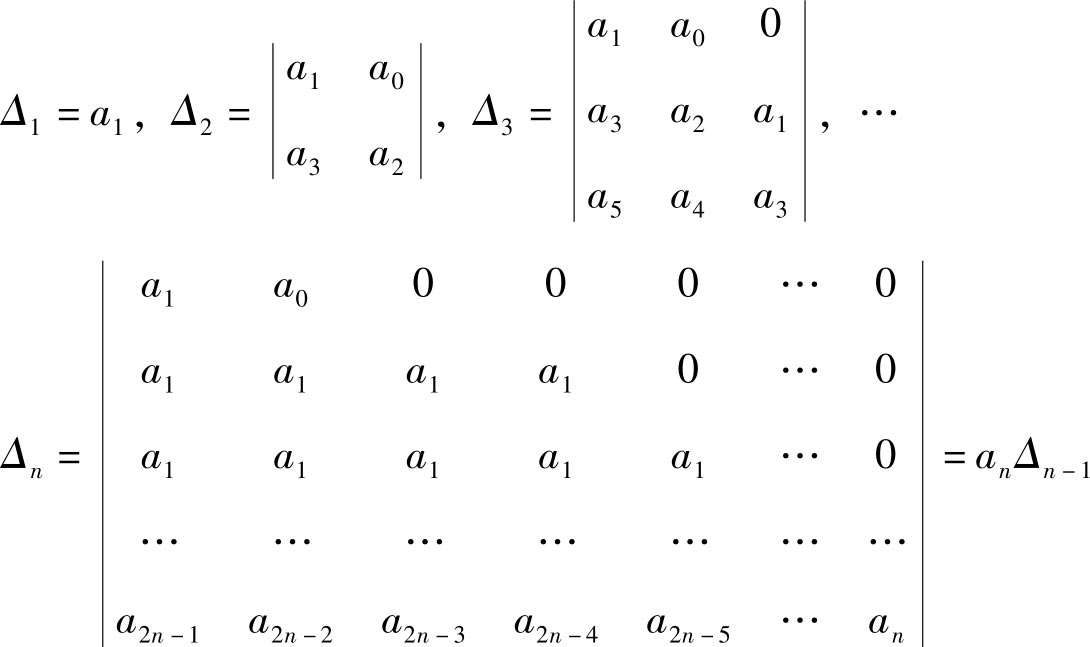
当 i > n ,规定 a i =0,如果 Δ 1 >0, Δ 2 >0, Δ 3 >0,…, Δ n -1 >0, Δ n >0同时满足,特征方程的一切根的实部为负,则连续系统处于稳定状态。
连续系统的劳斯(Routh)判据是判断系统的特征根是否在左半 s 平面来得到系统的稳定性,而离散系统的特征根的模全部小于1,即 z 平面的单位圆内,系统是稳定的。因此劳斯(Routh)判据不能直接用来判断离散系统的稳定性,需要引入一种线性变换完成从 z 域到 s 域的转换,才能将劳斯判据用来判断离散系统的稳定性。朱利(Jury)判据是离散系统稳定性的一个判据,首先计算出系统的特征方程式,如下式所示:
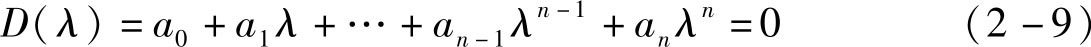
根据特征方程式的系数得到朱利(Jury)表
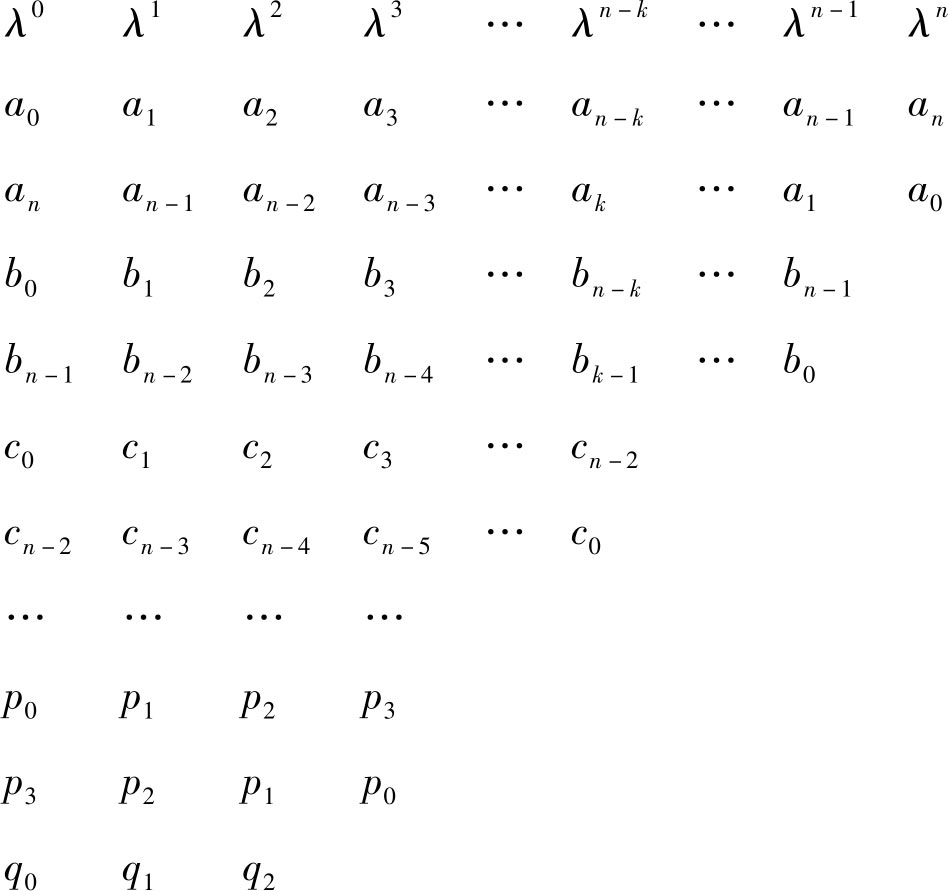
其中,
 ,
k
=0,1,2,…,
n
-1
,
k
=0,1,2,…,
n
-1
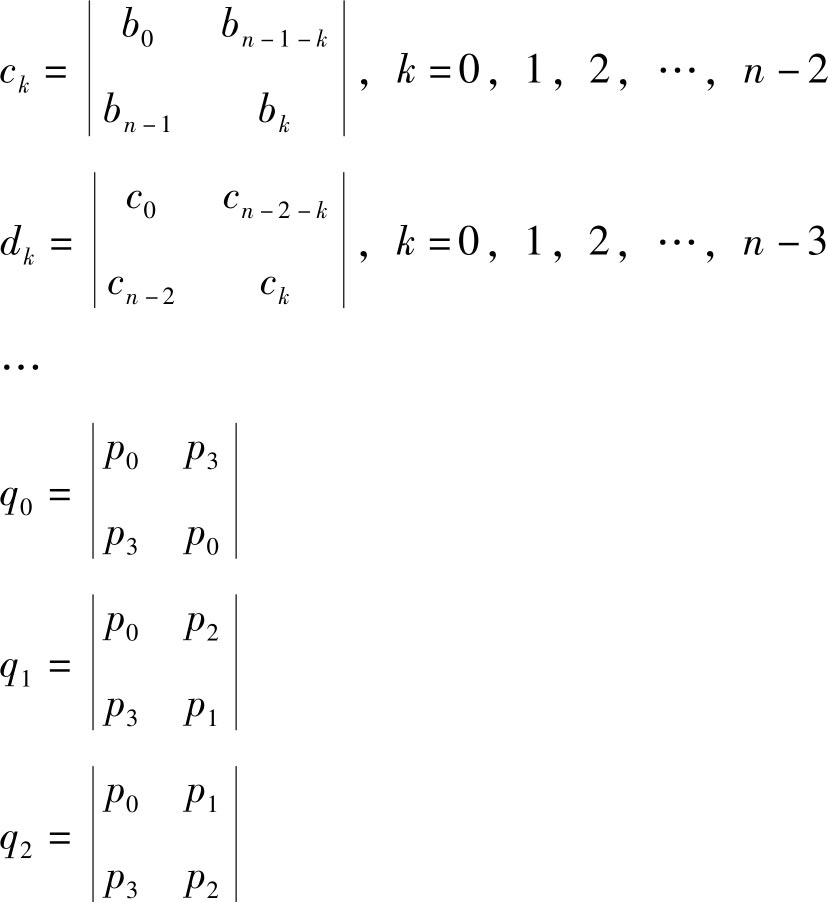
通过计算可以求得朱利(Jury)表中的2 n -3行 n +1列个元素,则满足下列三个条件时离散系统是稳定的。
(1) D (1)= D ( m ) m =1 >0.
(2)(-1) n D (-1)=(-1) D ( m ) m =1 >0.
(3) n -1个约束条件:
| a 0 |< a n ,| b 0 |>| b n -1 |,| c 0 |>| c n -2 |,…,| p 0 |>| p 3 |,| q 0 |>| q 2 |.
上面三个条件是离散系统稳定的充分必要条件,任何一条不满足,离散系统就不稳定。以下章节中系统的稳定域均是根据朱利(Jury)判据得到。
混沌现象具有确定性、非线性、非常复杂且具有内在随机性的运动轨迹,对初值敏感性使其运动轨迹不可预测。要根据系统的特点对混沌现象加以控制:①混沌对于系统的运行有害时,可以加以控制;②混沌对于系统运作有利时,创造条件使之产生特定的混沌轨道。总之,我们要利用混沌运动自身的特性达到控制目的。狭义的混沌控制是指抑制混沌的发生,可以定义为:根据不同领域的实际需要,设法从多种多样非线性系统所产生的混沌行为中,任意挑选几处所需的周期信号,甚至非周期信号,并实现有效控制。目前,对于有害的混沌运动,我们要采取一定的控制方法抑制或消除混沌运动的发生。对于很多经济管理系统,混沌对系统的运行是有害的。所以,要根据系统自身的特性采用有效的方法抑制混沌。
目前,对混沌的控制主要通过以下两种方法:①通过对参数的修改实现对混沌系统的控制;②通过系统状态变量的修改来抑制混沌的发生。OGY方法是最早用于抑制混沌发生的方法,Ditto,Rouseot和Span通过实验验证了OGY方法的有效性和不足之处。Ott,Grebogi与Romeras,Daywansa在Ditto,Rouseot和Span的基础上对OGY方法做了改进。许多学者相继提出了一系列混沌控制方法,如参数周期扰动法、周期激励法、OPF控制法、连续反馈控制法、自适应控制法等。混沌的控制与经典的控制不同,混沌控制的共同特点是尽可能利用混沌运动自身的特性来达到控制目的。各种方法各有优缺点,对于不同的学科领域,应用角度不同,根据具体情况可以采用不同的控制方法抑制或控制混沌运动。从控制原理来看,混沌控制方法大体可分为反馈控制和无反馈控制两大类。反馈控制的各种方法所需反馈控制量的大小可以根据受控系统的状态调节,因而具有微扰较小的优点;但一般需要预先了解系统的运动状态或目标态的性质才能控制。无反馈控制法在实际控制中不需要预先知道系统的动力学性质,具有较强的可操作性;但是控制量较大,必须始终作用在系统上。
结合本书所使用的对经济系统的混沌控制方法,主要介绍以下四种控制方法。
以离散系统为例来分析非线性动力系统的控制过程,系统如公式(2-10)。

其中, x k ∈ R n , k ∈ Z , μ ∈ R 是分岔参数。受控系统为
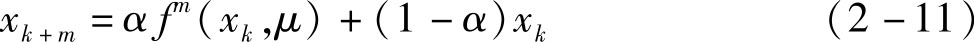
其中,0< α <1, m 为某个正整数, f m (·)是映射 f (·)的 m 次复合函数。选择适当的控制参数α可以控制给定周期轨道的稳定性,镇定混沌吸引子中的不稳定周期轨道。
在这里,考虑 m =1时系统(2-12)的稳定性控制条件,原系统在不动点处的线性化矩阵为:

不动点 x ∗ 稳定的条件为: J 1 的所有特征值| λ i |<1, i =1,2,…, n 。可以得到 x ∗ 稳定时分岔参数 μ 的取值范围。
系统(2-11)在 x ∗ 处的线性化矩阵为:
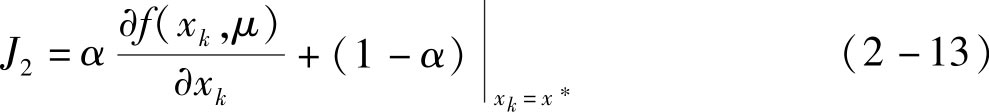
由于 J 2 中引入了调节参数 α ,只要选择适当的 α 值,就可以确保在失稳的不动点 μ 值范围内,可满足 J 2 的所有特征值| λ i |<1, i =1,2,…, n ;从而使不动点在更大的参数范围内保持稳定,延迟分岔和混沌现象的发生。
延迟反馈控制法的主要思想是让特定轨道的输出信号经过延迟时间后再输入系统中,作为延迟反馈控制的信号。延迟反馈控制的形式为: F ( t )= K [ y ( t - τ )- y ( t )]= KD ( t ),其中, τ 为延迟长度, K 为反馈控制因子。通过调节 K 和 D ( t ),可以使系统的李雅普指数小于零,达到混沌控制的目的。当 y ( t - τ )- y ( t )=0,则 F ( t )=0,不稳定系统轨道变成稳定轨道,而且没有改变系统的均衡解。延迟反馈控制法简单易行,在本书的研究中用来对风险规避型供应链的博弈模型的混沌轨道进行控制,使用非线性控制方法对二维离散混沌系统进行混沌控制。下面考虑一般的离散混沌系统:
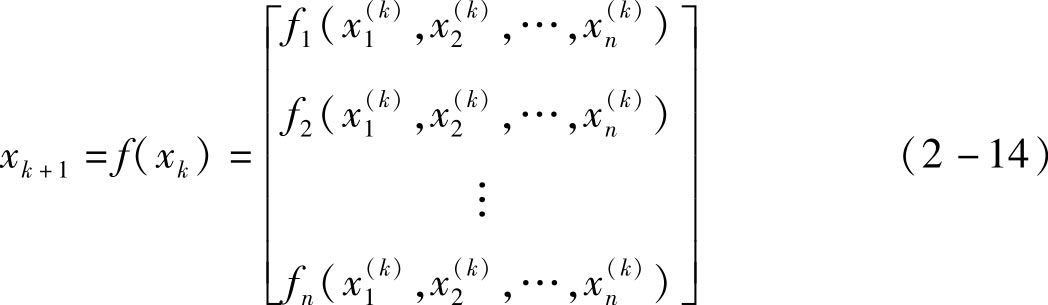
状态变量为
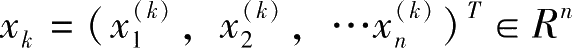 ,非线性反馈控制为
,非线性反馈控制为
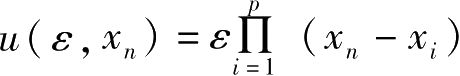 。其中,
ε
为反馈系数,{
x
i
}为特定的不稳定周期轨道,
p
为要控制的轨道数。被控制后的系统为:
。其中,
ε
为反馈系数,{
x
i
}为特定的不稳定周期轨道,
p
为要控制的轨道数。被控制后的系统为:
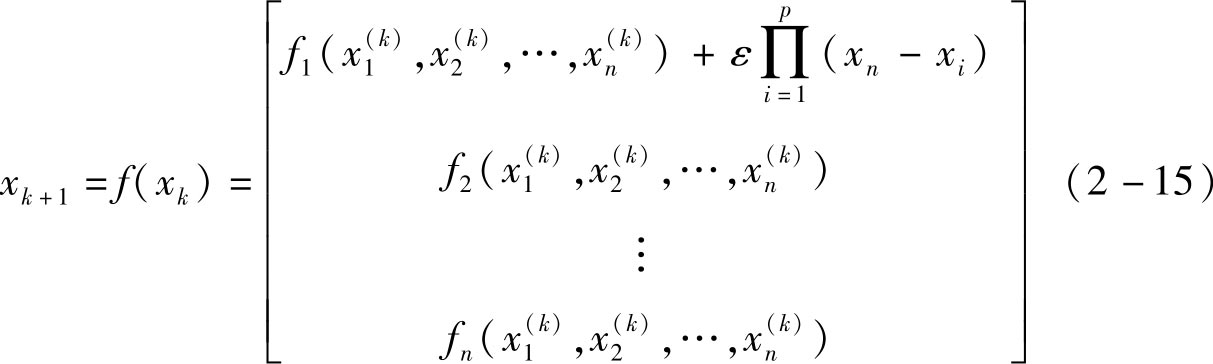
调整反馈系数 ε ,可以将系统稳定在固定点或其他任意周期轨道上。
以离散动力系统为例,设原系统为:
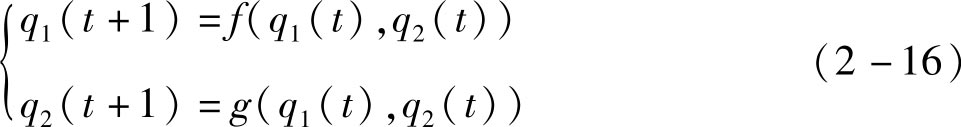
加入控制策略后受控系统为:
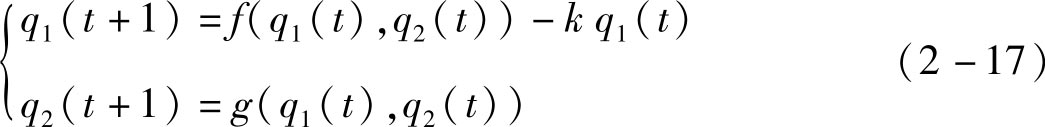
k 的取值范围较大,为了使系统回到稳定状态,需要适当的选择 k 值。
系统变量的脉冲反馈法由Guemez和Matias在1993年提出。这种方法的基本思想是当系统的控制参数不好确定或者不好找出时,改变系统变量来达到对离散系统映象和连续系统混沌的稳定控制。这种方法弥补了以上几种方法的不足,可以不受限制地改变系统变量。因为对于一个对初值敏感的混沌系统,有时候不好确定可调整的控制参数。下面将系统变量脉冲反馈法(PPSV,Proportional Pulses on System Variables)应用于离散系统的控制过程进行介绍。

其中, x ∈ R N ,为系统的状态变量。若脉冲反馈的反馈律为 g ( x n ),反馈步长为 k ,即每隔 k 次迭代,将 g ( x n )反馈到系统中去。一般地, g ( x n )采用变量比例反馈形式。
设 g ( x n )= Bx n , B =diag[ b 1 , b 2 ,…, b n ]为 N × N 脉冲强度向量,那么,可以得到方程:
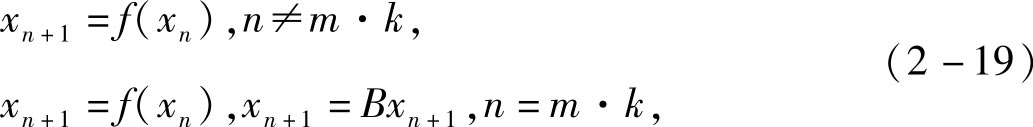
其中, m >1为自然数,选取适当的 B 和 k 就可以实现控制目的。