






想象一下台球桌上三颗球相碰撞的情形。如果一颗运动中的球撞击另一颗静止的球(或两者都在运动中),假设我们知道球的质量、运动速度,以及(或者忽略)摩擦力,根据牛顿定律,则可精确算出两颗球碰撞后的运动方式。但如果两颗静止的球彼此接触,而运动中的球从旁同时撞击到它们,则牛顿定律无法告诉你这些球在撞击后将如何运动。
 假设两颗静止的球其中之一先被撞到,哪怕只是0.01秒的差别,牛顿定律都可以告诉你它们将如何运动。但对于真正完全同时的撞击,牛顿定律就无能为力了。你可以试着摆脱这种困境,宣称现实生活中几乎不可能发生这种同时的碰撞。然而,小到钟摆的摆动,大至登月宇宙飞船的飞行运动,我们都能利用定理成功地解释,在这么简单的情况下,竟然无法预测碰撞后的结果,这实在让人很苦恼。
假设两颗静止的球其中之一先被撞到,哪怕只是0.01秒的差别,牛顿定律都可以告诉你它们将如何运动。但对于真正完全同时的撞击,牛顿定律就无能为力了。你可以试着摆脱这种困境,宣称现实生活中几乎不可能发生这种同时的碰撞。然而,小到钟摆的摆动,大至登月宇宙飞船的飞行运动,我们都能利用定理成功地解释,在这么简单的情况下,竟然无法预测碰撞后的结果,这实在让人很苦恼。
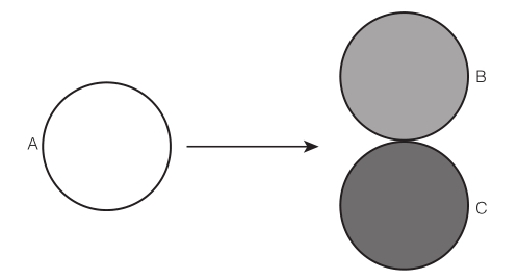
图1.1 根据牛顿定律,如果一颗具有完美弹性的球(A),同时撞击两颗相接触的具有完美弹性的球(B、C),我们是无法预测这三颗球在撞击后的运动方向的。
19世纪时,没有人真正担心这件事,大家都忙着利用牛顿定律以及伽利略与牛顿所发展出的科学方法,来描绘一个有秩序的、机械式的宇宙。拉普拉斯在1814年所写的《概率论的哲学理论》(Essai philosophique sur les probabilitiés)中的一段话,说出了当时的普遍看法:
想象有一个智慧体,它在任何时间都知道所有控制大自然的力量,同时也知道每一项事物的运动状态。假设这智慧体可以将所有数据加以分析,能把宇宙中大大小小物体运动的状态用一个公式描述。对它而言,没有不确定的东西;它可以清楚地看到未来与过去。
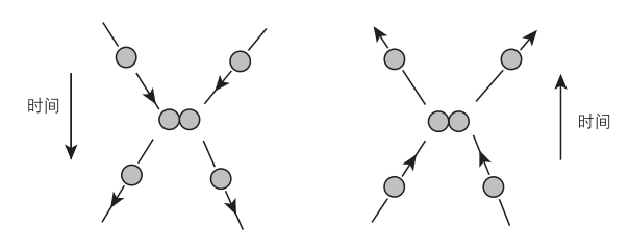
图1.2 根据牛顿定律,一对物体的碰撞是完全可逆的。无论“时间箭头”的方向为何,这个图看起来同样合理。
在现在,那样的智慧体会是一台知道宇宙中每个粒子的位置与速度的超级计算机,它可以运用牛顿定律描述自然界中的其他作用力(例如重力与电磁力),它不但可以预测每个粒子未来的运动方向,还可以推算出它们过去的历程——因为牛顿定律不涉及时间进行的方向,如果时间逆行,这些定律依然适用,就好像你可以想见两颗台球相碰撞之前,或是太阳系中每个行星在轨道上反向的运行情形。牛顿定律中没有时间箭头,而对拉普拉斯及其他人而言,它们似乎描述了一个对过去和未来都有严格规定的完全机械式的世界,在这个世界里,没有自由意志存在的空间。但这些人都忽略了一点:如果宇宙中的某时某处恰巧有三个粒子同时碰撞,这种论证的基础将不复存在。至于在这种情况下自由意志是否存在的问题,我想留给哲学家去讨论。
这个有关于时间的谜题,又出现在19世纪最伟大的物理成就——关于光以及其他形式的电磁辐射的研究中。这些研究被苏格兰学者詹姆斯·克拉克·麦克斯韦(James Clerk Maxwell, 1831—1879)带到顶峰,他对电磁辐射的描述源自于迈克尔·法拉第(Michael Faraday, 1791—1867)。法拉第发现了环绕于磁铁或带电物质之外的电磁场,而我们在普通的实验课中就可以目击这个“场”:将铁屑撒在平置于磁铁上方的一张纸上,轻轻敲一敲纸面,铁屑便会排出连接两个磁极的线,显示出对应于磁场的所谓的“磁力线”(lines of force)。法拉第首先提出,光线可由场力线和磁铁及带电物质所引发的某种振荡而产生,就像拨弄拉紧的小提琴的弦一样。然而,法拉第缺乏足够的数学才能,无法将他的想法发展成完整的模型。直到1861年,麦克斯韦才完成这个任务。当时他证明了包括光在内所有已知的电磁现象,都可被一组只包含四个等式的方程式所描述,即今日我们所谓的“麦克斯韦方程组”(Maxwell’s equations)。这些方程式规范电磁场与辐射的方式,正如同牛顿定律规范实在物体一样。原则上,它们描述了所有情况,使得我们能算出任何电磁效应的结果,虽然在比较复杂的情况下得多点耐心。麦克斯韦方程组描述了发电机与马达的运作方式,解释了为什么罗盘的针指向北方,以及两个带电物体在某个距离下的作用力(之前人们已知,电力、磁力和重力一样,都遵循反平方定律),还有其他更多现象。19世纪中期,所有物理科学所知的现象,都可用牛顿与麦克斯韦两人所发展出的数学工具来处理。麦克斯韦方程组最奇妙的一点是,它们能自动地产生出一个对光的描述。这些方程式原本是针对电磁现象设计的,但它们隐含了电磁波在空间行进的速度。这速度正好是测得的光速(这个数值在19世纪60年代已被测出,不久后测量的精确度便提高了),这使得人们确信光的传播也是以电磁波的形态进行的。
但麦克斯韦方程组中有两个令人好奇的特点,其中一个不久后带给物理界巨大的震撼,另一个直到最近都只被看成是一个特例。方程组中第一个奇怪的地方在于,它们给出的光速是常数,光速与光源和测量光速的人(或机器)之间的相对速度无关。根据方程式,如果你用手电筒照我,我们共同测量这道光的速度就是常数c。如果我们都站着不动,就没有问题。但如果你我以高速移动擦身而过,我们所测得的手电筒射出的光的速度,依旧是这个常数c。当我接近你(依据常识,你会认为我测得的速度应该是c加上你我之间的相对速度),或是当我远离你(依据常识,我测得的速度应该是c减去你我之间的相对速度),其结果都一样。就是因为麦克斯韦方程组推导出光以定速行进,不因观测者的运动而有所不同,从而引导爱因斯坦在1905年发表了狭义相对论,并于10年后扩展为广义相对论。本书不探讨相对论,仅指出它的存在及它所提供的比牛顿理论对运动物体及重力更完整的描述。相对论并未推翻或排挤牛顿物理学,只是将牛顿的观念纳入其中,并将物理世界的描述延伸至牛顿理论不足的地方,特别是以极高速运动的物体,或在强大重力场影响下的物体。但对于像地球绕太阳的运动,牛顿物理学的精准度已经极高,对于人类周围事件的描述就更加准确了。