






想要解开这个谜团,必须发展出一套新的语言(如同我们正着手介绍的)和一种理解物理世界的新思维模式。接下来故事的核心思维,就是“吸引子”(attractor)的概念。如果将气体排入一个盒子中,不管是经由我们前述移动间隔板的方式,或者在盒子壁上打个洞的方式,最终的结果是这些气体将达到平衡状态,均匀地散布于盒子中。这个状态即为这个系统可能达到的最大熵,而且不论气体怎么进入盒子,结果都一样,不管洞是打在盒子的哪一面,或是打在什么特定的地方。最终的平衡状态(也就是能量最低的状态)称为吸引子,因为整个系统的运行方式宛如被吸到这个状态。一旦达到这个状态,我们将无法分辨系统是如何变成这样的——并没有任何记录显示,系统如何进入最终的平衡状态。
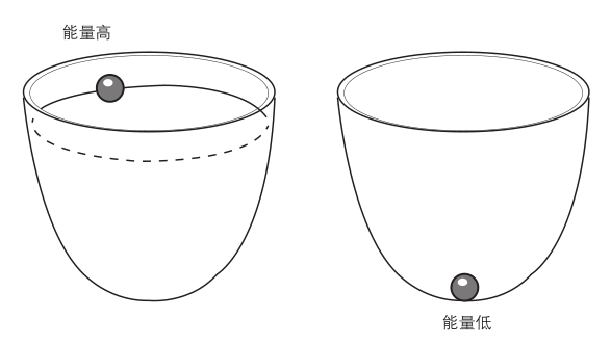
图1.4 若不受外界干扰,系统(甚至是简单到只包含一颗弹珠和一只大碗的“系统”)会倾向落入最小能量与最大熵的状态——前提是没有外来的能量。
这种方式也可以用来描述一些更常见的系统。如果让一颗弹珠在一只大碗里打转,经过回旋和振荡之后,弹珠会静止于碗底;这个状态就是系统的吸引子。即使在如此简单的系统中,吸引子也未必一样简单。如果弹珠在一个墨西哥宽帽上滚动,那么它将会静止于向上翘起的帽檐所形成的凹陷处。但圆圈形的凹陷处里的任何一点,都是吸引子的一部分(有时被称为“墨西哥宽帽吸引子”),因为它们都对应能量最低的状态。想象一个没有摩擦力的完美钟摆(即所谓理想钟摆),它的来回摆动也是一个吸引子。对摩擦力会消耗能量的真实钟摆来说,摆动会逐渐减速,最终完全停止,钟摆将垂直挂着,这也可被视为一个吸引子状态。不论钟摆如何运动(左到右、前到后,或是转圈),只要耐心等待,它终会达到相同的最终状态,而未留下任何先前的运动记录。用热力学的语言来说,当系统达到平衡状态时,就会忘记自己的初始状态。唯有它当下的状态才有意义。
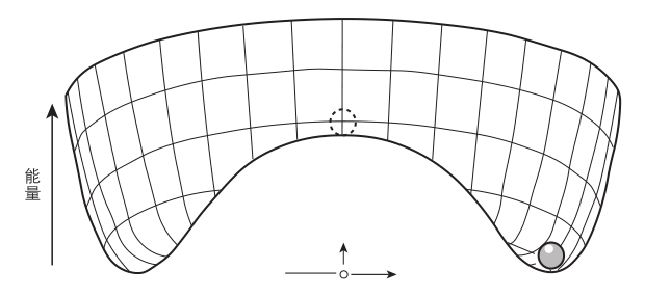
图1.5 系统趋向的状态称为吸引子。在图1.4的例子中,吸引子是位于碗底的一点。但吸引子也可以是个散开的区域,如图所示。丘上的弹珠势必落向谷底,而谷底的任何一点都是相同的吸引子。
但系统何时会达到平衡状态?在真实世界中没有所谓的完美隔热体,所以我们的气体盒子永远会不停地与外界交换热能。“摇荡的钟摆逐渐趋向静止”似乎是系统达到平衡的最佳例子。但即便如此,摆钟还是被冲撞而来的空气分子推挤着;即使把它放入真空室中,摆钟还是会透过吊绳和外界产生交互作用,因为它总要吊在某个东西上才能摆动。事实上,世界上没有孤立的系统(除了整个宇宙),也没有系统处于完美的平衡状态,系统可以很接近平衡——只要等得够久,要多接近就有多接近——但永远达不到所谓完美的平衡。
这些不只是空谈。借用普里戈金和伊莎贝拉·斯唐热(Isabelle Stengers,1949—)的一项实验,如果两个容器之间用一根细管连接,并放入氢气与硫化氢的混合气体,在相同温度下,当达到平衡状态时,两种气体在两个容器的混合比例一致。但如果其中一个容器的温度略高于另一个时,混合的气体将开始分离,较轻的氢分子会聚集在较热的容器中,而较重的硫化氢分子会聚集在较冷的容器中(同样的情形会发生在任何两种分子量不同的气体之间,并不局限于氢与硫化氢)。只要稍稍偏离平衡状态,就能由混沌中产生秩序。在平衡状态之外,适当情况下,能量的流动会自发性地创造出秩序来。这对我们自身的存在是极其重要的认知,因为无可否认的,我们是有秩序的生物,而同时有太多的证据显示,宇宙起始于一个没什么秩序可言的状态。
一般来说,接近平衡的系统会被导向“熵值增加率为最低”的状态。但这个观念直到20世纪才变得清晰起来。如同牛顿之后的物理学家首先专注于利用牛顿的公式与运动定律解决可处理的简单问题(因为它们最容易解答),热力学家先是专注于平衡系统,他们发展出一些定律和公式(像是热力学第二定律)。经由这个途径,他们发展并了解了热力学,并且将其研究范围延伸至统计力学。
这些研究大部分都试图利用数学来描述气体行为,因为气体分子的碰撞大致符合牛顿定律,是相对简单的系统,比较有可能在其中找到方程式的解。我们现在所知道的气体动力学,是由19世纪下半叶几位相互影响的科学家所发展出来的。研究主轴起于鲁道夫·克劳修斯在1858年提出的“平均自由路径”,意思指在特定的温度与压力条件下,气体分子在两次碰撞间平均移动的距离。他也提出了分子的“效应半径”的概念。麦克斯韦继承了这些观念,并加入分子碰撞时速度被限制于一定范围内的条件,在此基础上,他做了更进一步的研究。他表示,在适当界定这些性质后,许多被观察到的气体行为可以用简单的方程式表达。接下来,麦克斯韦的研究启发了德国的玻尔兹曼。玻尔兹曼将前人的成果集大成于统计力学的最初版本。在大西洋彼岸的美国,约西亚·威拉德·吉布斯(Josiah Willard Gibbs,1839—1903)也对这个科学新领域的发展做出了重大贡献。