第一章
概述

第一节
问题的提出

一、线性回归分析回顾

传统的回归分析，用一个模型描述一个因变量（被解释变量）和一组自变量（解释变量）之间的线性关系。其因变量（被解释变量）只有一个，自变量（解释变量）可以是一个或多个。

（一）模型形式

传统的回归分析中，模型如（1.1）式或（1.2）式。

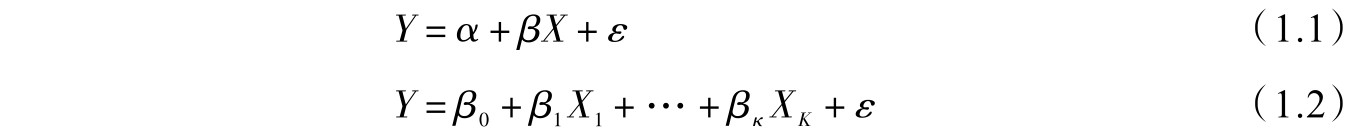
其中， β 是回归系数， ε 是随机干扰项。

（二）模型的基本假定

传统的回归分析中，对数据和模型有下面的基本假定：

1． X 是非随机变量：这意味着， X 是严格外生的，与 ε 无关。

2． X 与 Y 存在真实的线性关系。

3． ε 满足独立同分布，也就是随机干扰项通常服从正态分布，相互独立并具有同方差，满足三性：正态性、独立性、同方差性，也就是 ε ∼ N （0, σ ² ）。

二、实际应用中的问题

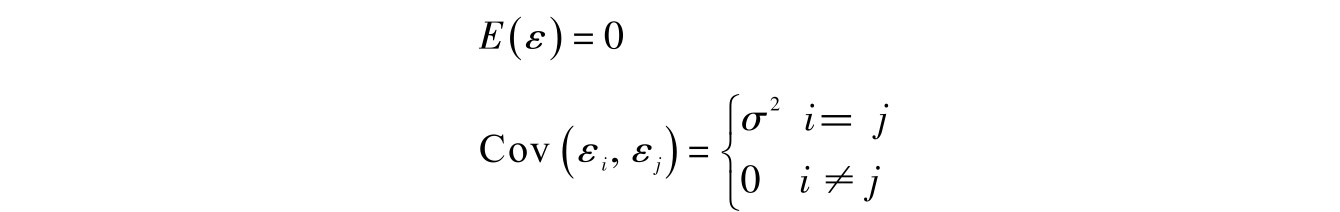
1． X 为随机变量

回归分析中，假定 X 为非随机变量；若实际中 X 为随机变量，即存在测量误差或 X 为潜在随机变量，不可以直接观测，模型将如何建立？参数如何估计？模型如何检验？

2．多指标变量之间关系复杂

在许多实际问题中，多个指标变量之间的关系往往比较复杂，并不一定都能够用一组自变量去解释一个因变量，如学历或受教育程度会影响其收入，而收入又会影响到消费支出的多少和消费结构，因此，学历或受教育程度就间接影响消费支出的多少和消费结构。多个变量之间不仅存在直接影响，还存在间接影响，如何建模？

3．潜在因子之间不相互独立

探索多个指标变量中存在的理论变量，即潜在因子之间关系时经常会用因子分析，而因子分析要求潜在因子之间相互独立，而实际问题中，有些潜在因子之间存在因果关系或一定的关联或依存关系，这种情况如何建模？

这些问题的存在，使得人们不得不探讨新的方法，即研究潜变量之间关系的方法。结构方程模型正是一种分析研究不可直接观测的潜变量之间结构关系的方法。

所谓线性是指所有变量，包括潜在的变量和可观测的变量之间的关系能够被表示在线性方程中，或者能够被转化为一种线性的形式。这个线性方程体系被称为结构方程模型（Structural Equation Model, SEM）。在后面的介绍中，可以看到，结构方程模型主要通过协方差矩阵完成模型建立，因而也被称作协方差结构方程模型（Covariance Structure Model, CSM）。 lSoB3xwHONq0ZwKfO6KtBzW5h0bggqm7oSoT4X3JJJCa0IKoxjc5zHpQARXtMHk2