




公共场所是指由于人口密度大、人员活动集中、物的流动稠密、信息交换频繁从而易于发生各种事故和灾难的公共建筑或场所。
按使用性质划分,可分为教育、科研类,如:各类学校,幼儿园,科研机构等;文化、娱乐类,如:文化宫,博物馆,青少年活动设施,电影院等;体育、休息类,如:体育场(馆),游憩设施等;医疗、卫生类,如:各类医院等;商业、服务类,如:百货商店,大型商场等。
按人口在空间分布层次划分,可分为受限空间类:高层建筑、地下商场、室内体育馆等;开放空间类:商业街、集贸市场等。
受限空间类公共场所最大特点就是安全出口有限,给紧急情况下的人员疏散带来很大困难,在此类公共场所中,最大安全隐患是火灾,一旦发生火灾,直接烧死的人很少,绝大多数是因为无法及时逃生而被火灾的烟气毒死和窒息而死,还有由于人群急于逃命而造成的拥挤踩踏或从高处坠落造成的伤亡。
城市公共场所事故灾害的一个显著特点是有大量人群聚集,一旦发生公共事故,由于缺乏控制及管理,往往会造成较大的人员伤亡,并使公共场所事故灾害扩大化。在这里把公共场所中可能发生的事故定为由于人群聚集所引发的事故,如因观众的争吵而导致的秩序混乱,或发生争执甚至暴力等。公共场所事故以人群聚集为条件,由于公众在公共场所事故及意外事故中,存在从众心理及盲目恐慌,往往使事故难以控制并有导致灾害扩大化的趋势,或引起某种次生事故灾害。
导致人群拥挤踩踏事件的因素很多,如图2-29所示,一般可以分为场所的类型和设计,人群的类型和行为,人群聚集场所的管理等。本文分别从人群的密度与速度,人群的受力状况,运动人群中的信息传播,人群的组成及大小等方面进行分析,用于在现实中指导人群管理。
1.人群密度
人群拥挤踩踏事故发生的一个基本条件是人群高度密集。人群密度与人群运动速度密切相关,密度的增加会使得人的运动速度下降甚至发生堵塞。Wertheimer(2000)指出,一旦人群密度超过了临界值,个人和人群就处在风险中。Still认为,对于静止的人群,人群安全的临界密度为4.7人/m 2 ;对于运动的人群,安全的临界密度为4.0人/m 2 。
拥挤踩踏事故周围的人群密度可以分为三个层次:自由运动区,限制运动区和运动停滞区。运动停滞区的人群密度应在4.0人/m 2 以上,运动几乎处于停滞状态,运动时断时续;限制运动区的人群密度处于0.5~4.0人/m 2 之间,该部分人群相互影响,运动速度在0.5~1.0m/s之间;处于外围的人群属于自由运动人群,其运动速度为自由运动速度(1.34 m/s左右),行人间无相互影响。人群拥挤事故的发生点通常在运动停滞区,由于窒息、中暑、滑倒、骚乱等原因,诱发了事故的发生,人群拥挤事故发生时,事发点处由于有人突然跌倒,人群中出现波动,随之产生多米诺效应。事故点临近区域人群因惯性或来自后面的推动力也叠加到已经跌到的人(人群)上;没有获知信息的人群由于信息缺乏而继续前进,导致距离事发地点附近的人群密度越来越大。随着触发事件的发生,处于事故发生地点附近的人群密度增大到一定程度后(同时伴随着信息的传播),处于中间区域的人群运动速度减缓,或者向与事故发生方向相反的方向疏散,该区域混乱度增大,且范围扩大。
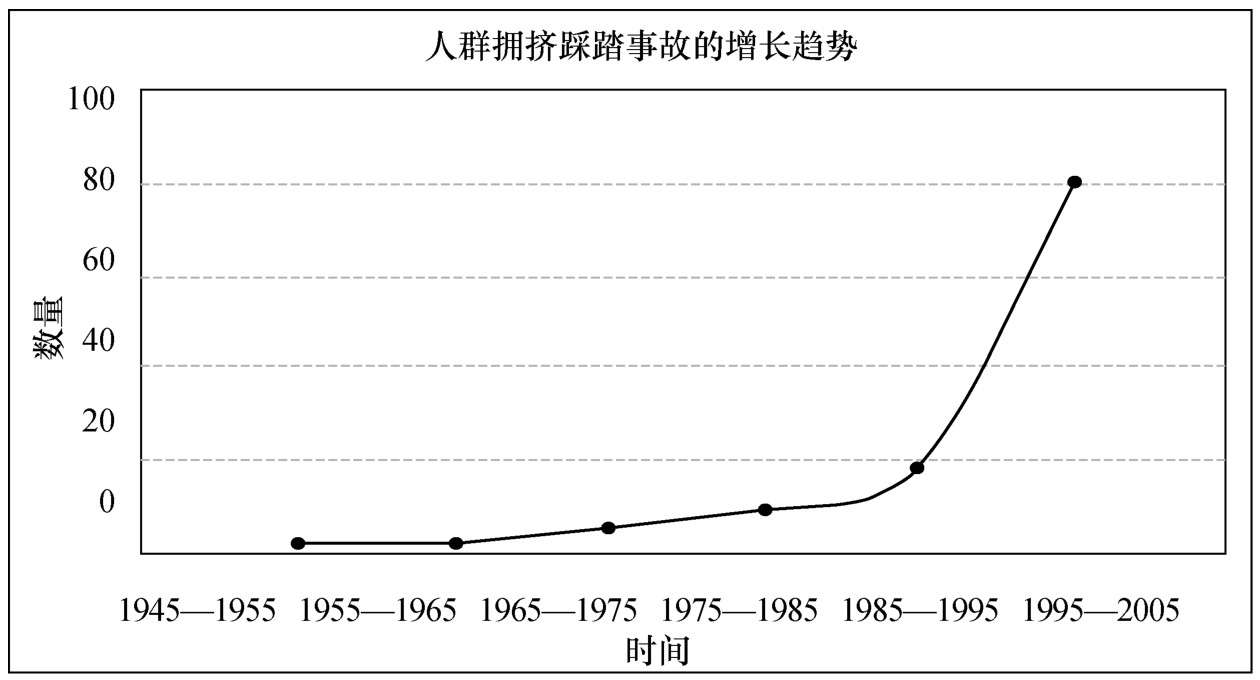
图2-29 人群拥挤踩踏事故的增长趋势
拥挤事故发生点的初始密度值可能处于限制运动状态或停滞状态。但事故发生后,由于信息的缺乏和人群的恐慌,聚集密度会在短时间内急剧上升,甚至达到8人/m 2 以上。此时,个体将失去控制,人将成为人群中的一部分。研究表明,当人群密度为7人/m 2 时,人群具有流体的性质。人群中的震荡波通过人群进行传播,使得人们双脚离地,震荡距离可以达到3m甚至更大。强大的人群压力,恶化的焦急情绪,使得人们呼吸困难。人体周围不能传播身体散发出的热量,会使人们虚脱或者昏倒。
2.拥挤踩踏事件中力的作用
拥挤的人群中可以产生不可承受或不可控制的力。研究表明,拥挤踩踏事故中的人群死亡主要是由压力导致的窒息。事故过后,现场因压力而弯曲的钢质扶手表明,这种力要超过4500 N。这种力的产生是来源于推挤和因多米诺效应而叠加的身体重力。拥挤踩踏事故中的人群拥挤有两种类型:人群在垂直方向上相互堆叠和水平方向的相互拥挤。在辛辛那提摇滚音乐会事故中,人体堆积的长度达9m。人群之间的压力主要来自于后面人群推动力及墙壁向后的反作用力。对由于身体倾斜和推挤而对护栏产生的力进行的试验表明:30%~75%是由参加者的体重产生的。研究表明,在恐慌状态下,5个人能够产生3430 N的力。
D.Helbing对人群的疏散时间与期望速度之间的关系进行了研究,如图2-30所示。当期望速度小于1.5m/s时,人群疏散时间随期望速度增加而增大;期望速度高于1.5 m/s时,疏散效率开始下降。这是由于推挤,导致摩擦力增加而产生的后果。此外,当期望速度为5 m/s时,如图2-30虚线部分,如果作用于他们的径向力的总和除以他们的周长超过1600 N/m,行人开始出现受伤现象并且不能运动,成为其他人运动的障碍。
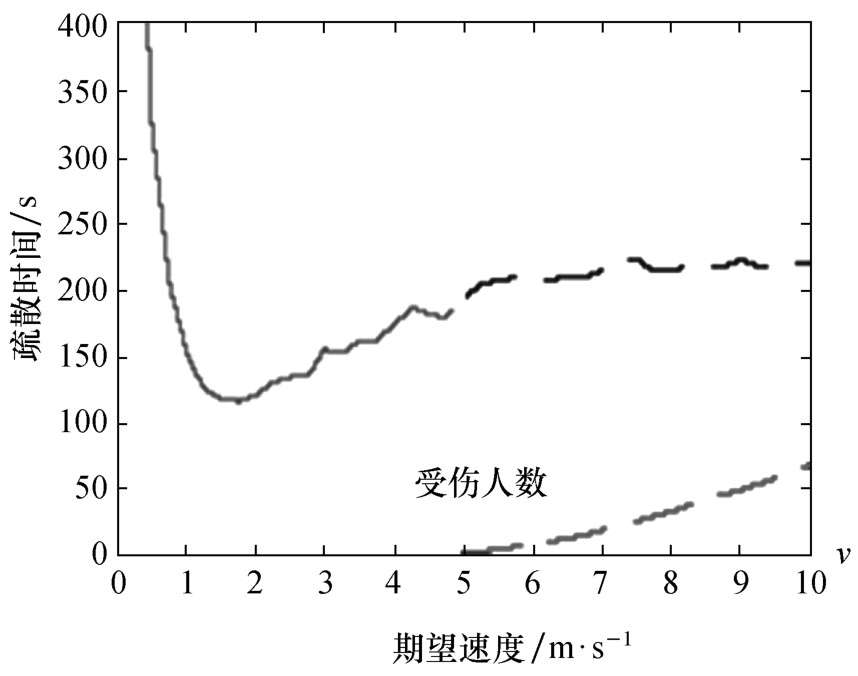
图2-30 疏散时间与期望速度关系
3.人群的恐慌
在触发事件发生后,人群会产生严重的恐慌情绪,恐慌对人群拥挤踩踏事故的影响主要表现为两个方面:一方面,恐慌状态下的人群会产生诸如推挤、超越他人等不理智的行为,从而使事故急剧恶化;另一方面,恐慌会使人由个体行为为主转化到以从众行为为主。
研究表明,恐慌对人群的作用是两方面的。适度的恐慌有利于加快人群疏散速度,有利于人群逃生。当恐慌度低于0.4时,以个体行为为主,表现出理智;当恐慌度大于0.4时,个体随恐慌度增加而表现出越来越强的从众行为,理智丧失,拥挤踩踏事故发生时,人群处于极度恐慌状态下,期望速度高,相向运动多有发生,从而使拥挤踩踏事故的后果加剧。
4.人群的大小
人群的大小与事故的后果之间也存在着密切的关系。这主要是因为:由于人群变大,一旦开始运动,停下来或改变方向需要很长时间,从人群中开始出现波动到恢复稳定状态需要的时间增加。其间很容易因某些突发事件而出现失控,而拥挤事故很可能在其间发生。研究表明,事故的持续时间非常短,事故发生时犹如爆炸冲击波的速度冲击人群。如果人群过大,可能会使事故的后果加剧。
5.信息交流
信息交流分为管理人员之间的交流、管理人员与人群之间的交流、人群内部的交流,人群踩踏事故中的通信主要指前两者。
心理学家把人群比作相互啮合的,具有某种行为的多个个体的集合,每个个体周围都形成小的群组,群组成员之间互通信息,每个群组中都有一个处于支配地位的成员。群组的成员并不知道整个人群中正发生什么,所以处于支配地位的个体可能影响其他个体的行为。相邻的群组和群组之间可以互通信息,如图2-31所示。群组之间传播的信息可能是传闻和错误的信息(如谣言),这可能导致人们不期望行为的发生。
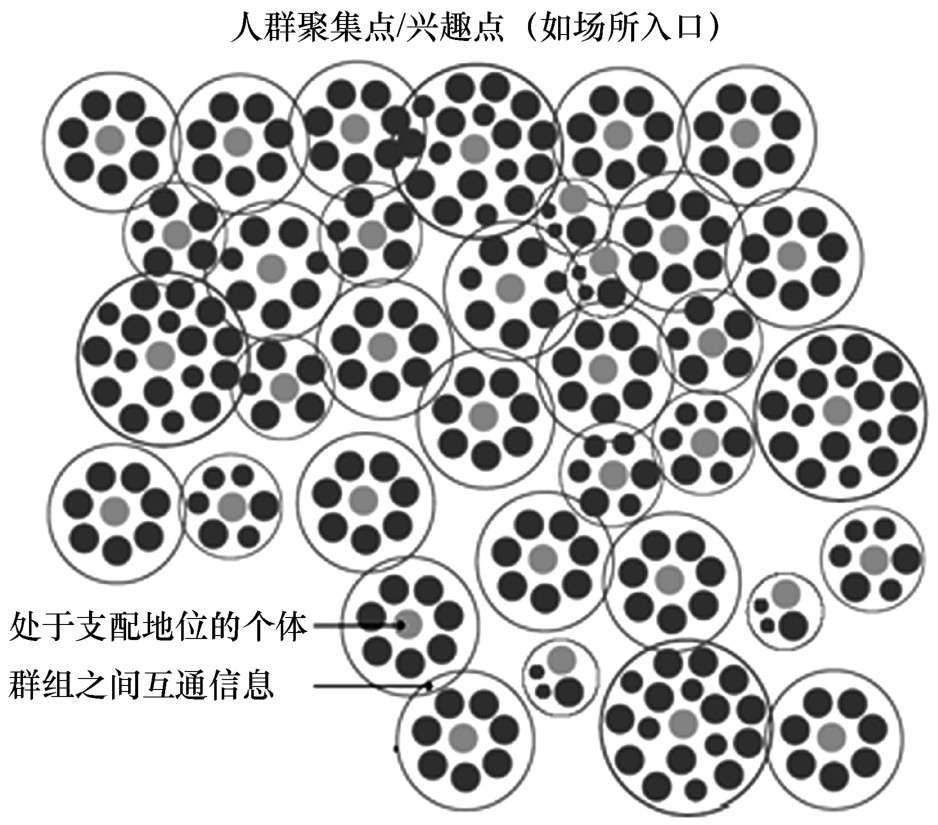
图2-31 人群间的信息交流
通常,人群缺乏对信息的前后比较。事故发生前,在后面的人群处于低密度自由运动状态,而前面的人群已经处于不稳定和高压力状态。当前面的人群已经发生了严重的灾难时,后面的人群常因信息缺乏而表现出不适当的行为。前面队列的崩溃给出一种向前运动的错误感觉。这类问题的唯一管理方法是对后面的人群进行管理,而不像普通的人群管理方法中对前面人群进行管理。因人群过大产生的通信缓慢或通信困难而带来的问题,可以采取对侧面人群和后面人群进行控制来减缓。
人群拥挤踩踏事故的现实风险由固有风险和风险减缓因子构成,其中固有风险由原发事故风险和风险扩大因子构成,如图2-32所示。
人群拥挤踩踏事故的现实风险=原发事故风险×风险扩大因子×风险减缓因子。
其中固有风险与以下因素有关:场所类型、活动类型、人群性质、人群组成、人群的数量、人群密度、场所管理、社会状态(和平稳定或战争以及是否具有种族仇恨)和自然灾害等。风险扩大因子和风险减缓因子可以看作控制因子,当管理完善,人群的整体素质高,安全意识强时,该因子就是风险减缓因子;反之则为风险扩大因子。
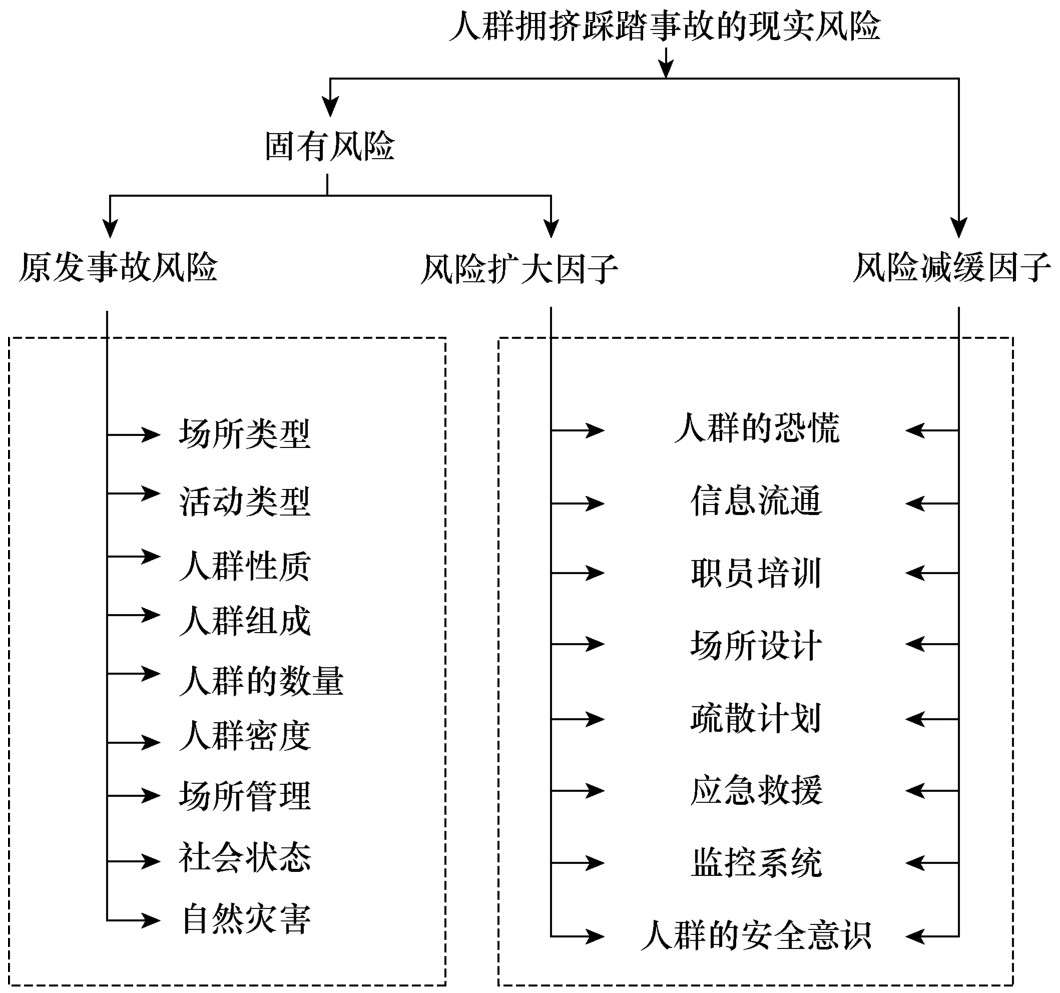
图2-32 人群拥挤踩踏事故现实风险指标体系
体育赛场历史事故统计分析表明出口堵塞为导致疏散人群拥挤踩踏事故发生的主要原因,滞留阶段是人群疏散过程最常见的一种人流形式,同时也是拥挤踩踏事故风险的主要承载体。本部分基于人群流量与人群密度关系建立了时间维变量的滞留人数定量模型,通过设定体育赛场看台不同宽度出口人群疏散实例计算分析结果表明,滞留人数不仅对人群疏散时间有直接影响,而且与事故发生概率之间存在一定的关系。
1.滞留人数定量模型基本参数分析
(1)模型基本参数。
影响出口滞留人数的基本参数为人群流量 F ,其为人群流动系数与出口宽度的函数,而人群流动系数又与人群移动速度与人群密度有关,表示如下:
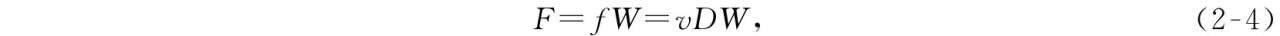
式中, F 为特定时间间隔内通过出口的人群流量,人/s; f 为人群流动系数,单位时间、单位出口宽度通过的人数,人/(s·m); v 为人群移动速度,m/s; D 为人群密度,人/m 2 ; W 为出口宽度,m。
由式(2-4)可以看出,人群流量与人群移动速度、人群密度和出口宽度有关,出口宽度一般为定值。人群移动速度与密度的关系许多学者都进行了大量的观测研究,比较典型有日本K.Togawa,俄罗斯Predtechenski和Milinskii,加拿大Paul及《SFPE消防工程手册》等。上述模型基本上都是为研究疏散问题而根据经验或试验数据统计得到的,一般来说没有考虑出口完全堵塞的情况,国内刘禹等人在相关假设条件下构建了拥挤状态下人群密度与人群速度关系模型,模型考虑当人群密度达到一定值时,出口人群流量为零,而由赛场出口事故原因分析可知,出口区域人群密度非常高时,出口会出现堵塞情况,因此本定量模型是基于人群流量参数在某特定密度下取零的条件建立的。
(2)模型基本参数关系分析。
许多学者对人群移动速度与密度的关系都进行了大量的观测研究,除了前面对疏散时间计算公式的研究者外还包括英国的Keith Still,荷兰的W.Daamen和Hoogendoorn,香港的S.M.Lo以及国内刘禹等人。其中许多研究都有相似之处,选取有代表性的研究总结如图2-33所示。
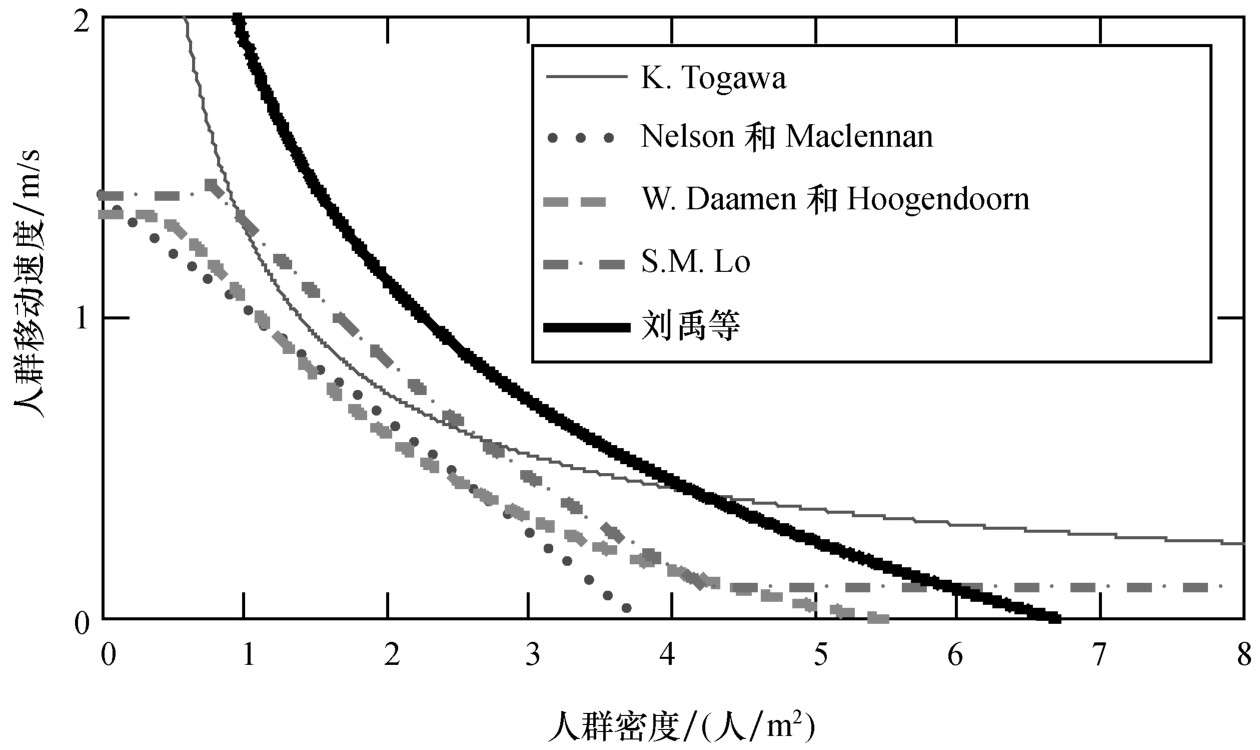
图2-33 人群移动速度与人群密度经验关系总结
而人群流动系数通常表示为人群密度和人群移动速度的函数,因此根据图2-33可以得到人群流动系数与人群密度的关系,如图2-34所示。
由图2-33和图2-34可知,由于研究对象及现场观测方法等的不同得出的关系曲线也存在一定的差异。一般来说可以将人群密度和人群移动速度的关系描述成对数关系,也可以描述成指数甚至线性关系。但所有研究表明,如果人员的移动速度大,必然要求的人口密度小,而相应的人群流量不一定大,反之,人群密度大,但速度又会降下来,流量也不一定大,人群流量只有在某一人口密度的条件下达到最大。
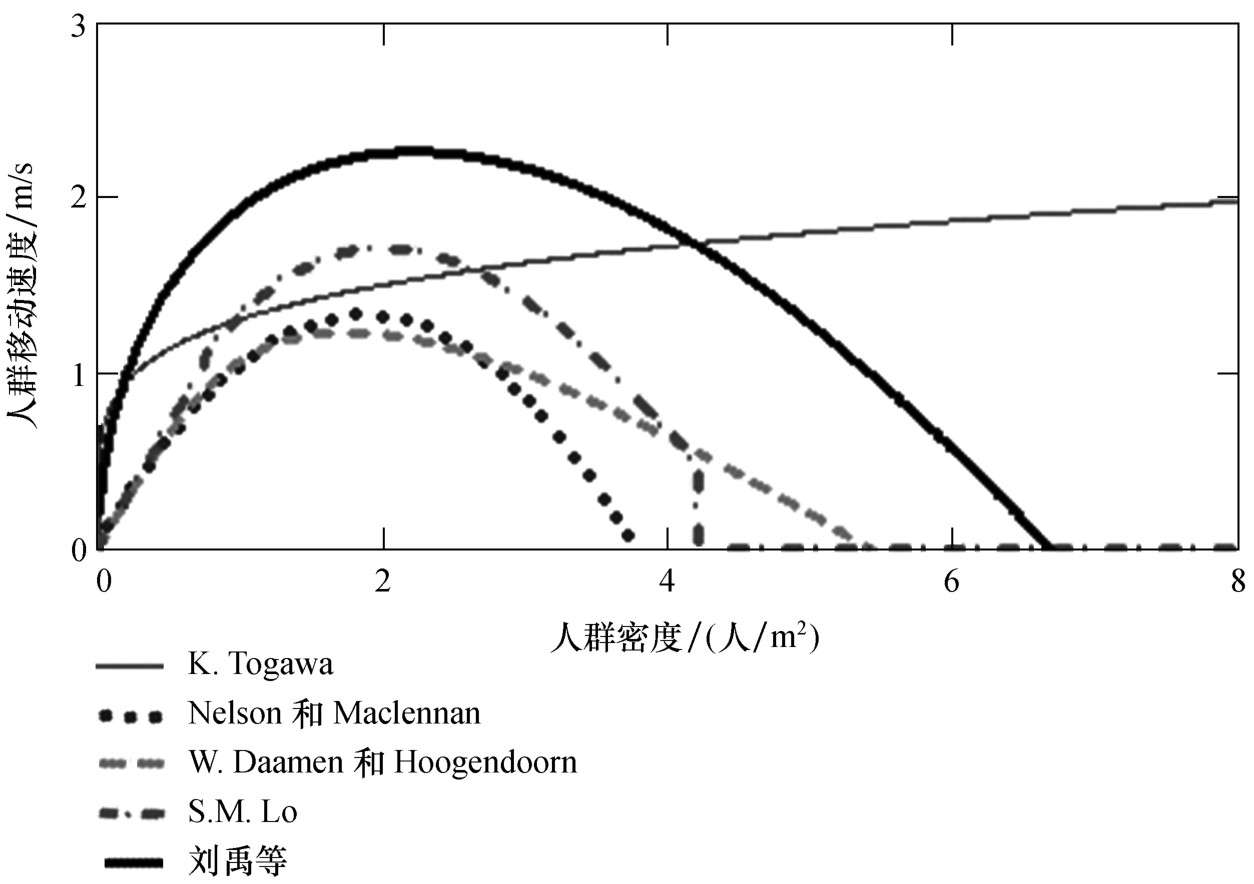
图2-34 人群流动系数与人群密度的经验关系总结
2.滞留人数定量模型的建立
赛场恐慌人群进行疏散是在假定体育赛场事故灾害(如看台倒塌、恐怖袭击等)已经发生的条件下,恐慌人群通过狭窄通道或出口处时可能发生拥挤踩踏事故,基于此原理提出了对恐慌人群拥挤事故进行定量风险分析的模型。模型从人群密度与移动速度之间的关系着手,分析了出口人群流动系数随密度变化的规律。拥挤踩踏事故发生的一个重要特征就是特定区域人群高度聚集,也就是该区域聚集人数多少决定了此类事故风险的发生概率。因此本文提出了基于时间维变量的滞留人数模型来表征人群聚集风险的易发程度。
依据日本Togawa推导的建筑疏散时间公式及其他相关理论,在人群疏散方向上取一基准断面P,则向断面P前进的人群称为流入群集;流出断面P继续前进的人群为流出群集,如果由于某种原因,例如通路变窄,或遇到门、楼梯、台阶等通道性质的改变,便容易引起人群在基准断面P处的滞留与混乱,在断面P处滞留的人群称为滞留群集,它等于流入群集与流出群集人数之差。
考虑赛场水平通道人群疏散场景:多个分支入口,一个出口,通道内人群流动呈直线型,通道出口在 t 时刻的聚集(滞留)人数 N A 如式(2 - 5)所示:
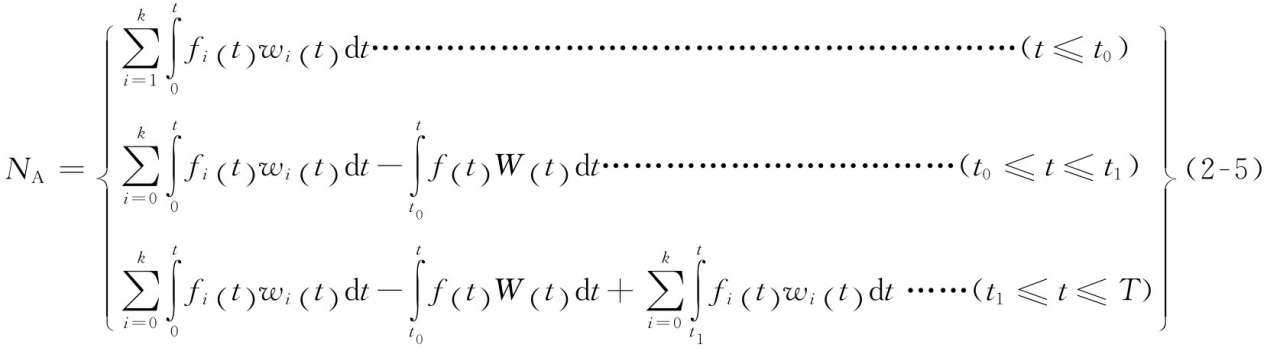
式(2-5)中, f i ( t )为通道第 i 个分支入口 t 时刻的人群流动系数(单位时间内单位空间宽度通过的人数),人/(m·s); f ( t )为通道出口 t 时刻人群流动系数,人/(m·s); w i ( t )为第 i 个分支入口 t 时刻人流宽度,m; W ( t )为通道出口 t 时刻人流宽度,m; k 为通道分支入口数目; t 0 自疏散开始至出口断面P处刚出现人群滞留的时间; t 1 为通道出口人群流动系数 f =0的时间; T 为最后一人从分支入口进入通道的时间或出口区域达到饱和密度的时间。
3.赛场出口实例分析
选取某奥林匹克中心体育场看台其中一个出口区域,如图2 - 35所示。设计为七个看台的观众从此出口疏散到安全地带。
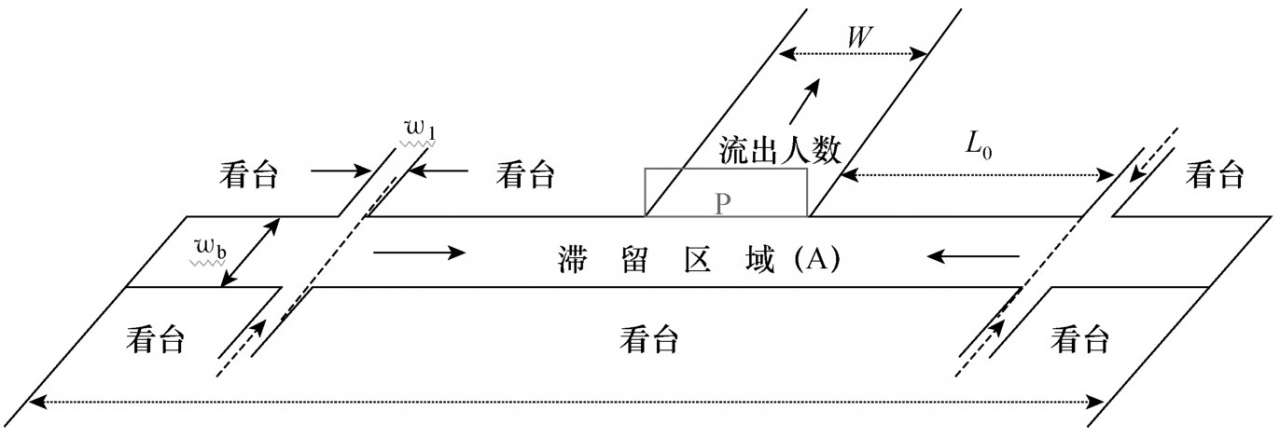
图2-35 某奥林匹克中心体育场看台人群疏散示意图
(1)初始设置。
人流宽度设定:看台纵走道宽度 w l 设为两股人流宽度(单股人流为0.5 m),横走道宽度 w b 设为四股人流宽度( w b =2.0 m),出口通道宽度设为 W 。
距离和面积设定:出口与最近的看台通道距离 L 0 按15个座位来算为15×0.6(座位宽)=9 m,出口附近区域面积 A = w b ×(2 L 0 + W ) m 2 。
看台人数设定:看台按20(排)× 15(座位数)=300人计算,因此总的疏散人数为2400人。
(2)相关假设及疏散场景描述。
纵走道出口人群流量设定:本模型不考虑观众从座席到纵走道的疏散,只考虑纵走道出口流量,《体育建筑设计规范》及相关体育建筑设计资料设定中国单股人群流量为40~42人/min,本研究人群流量 F′ 取40人/min,也就是单股人流每1.5秒通过一个人。
疏散场景设定:观众首先从座位看台纵走道出口进入横走道,然后通过出口通道疏散到安全地带。由于人数为正整数,由(1)分析可知每1.5秒单股人流从纵走道走出一个人,所以设此模型的时间间隔Δ t =1.5秒,疏散时间 t =1.5 n ( n =1,2… N )。
(3)滞留人数计算。
通过体育场水平出口通道的滞留人数可以通过下式来计算:
① 当 t ≤ t 0 ( t 0 = L 0 / v′ ):
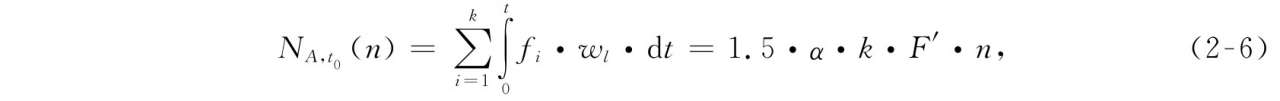
式中,
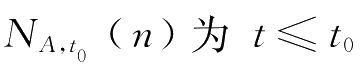 时刻水平通道出口区域(
A
)在时刻
t
(
n
)的滞留人数,且
t
(
n
)∈[0,
t
0
];
v′
疏散过程个体期望疏散速度;
v′
=1.5 m/s;
α
为看台出口人流股数,
α
=2;
k
为看台出口数目,
k
=4。
时刻水平通道出口区域(
A
)在时刻
t
(
n
)的滞留人数,且
t
(
n
)∈[0,
t
0
];
v′
疏散过程个体期望疏散速度;
v′
=1.5 m/s;
α
为看台出口人流股数,
α
=2;
k
为看台出口数目,
k
=4。
② 当 t 0 < t ≤ t 1 :
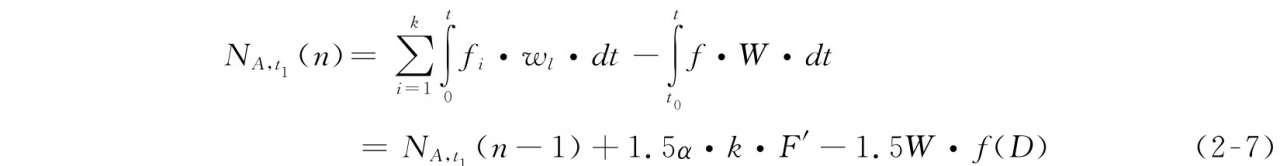
式中,
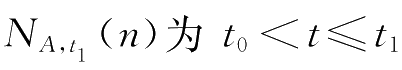 时刻水平通道出口区域(
A
)在时刻
t
(
n
)的滞留人数,且
时刻水平通道出口区域(
A
)在时刻
t
(
n
)的滞留人数,且
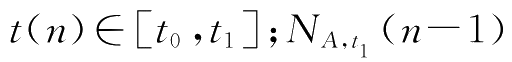 为
t
0
<
t
≤
t
1
时刻水平通道出口区域(
A
)在时刻
t
(
n
-1)的滞留人数,且
t
(
n
-1)∈[
t
0
,
t
1
];
f
(
D
)为水平通道出口人群流动系数,其为人群密度的函数,此处假设出口区域附近(
A
)人群密度是相同的,人群密度可以用下式表示:
为
t
0
<
t
≤
t
1
时刻水平通道出口区域(
A
)在时刻
t
(
n
-1)的滞留人数,且
t
(
n
-1)∈[
t
0
,
t
1
];
f
(
D
)为水平通道出口人群流动系数,其为人群密度的函数,此处假设出口区域附近(
A
)人群密度是相同的,人群密度可以用下式表示:
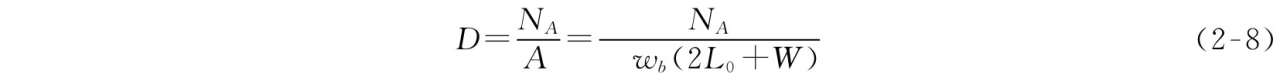
③ 当 t 1 < t ≤ T :
此时出口的人群流动系数在 t 1 时刻为零,也就是说此出口没有人员能够疏散出去。假设出口区域( A )人群密度最大为 D′ ,则
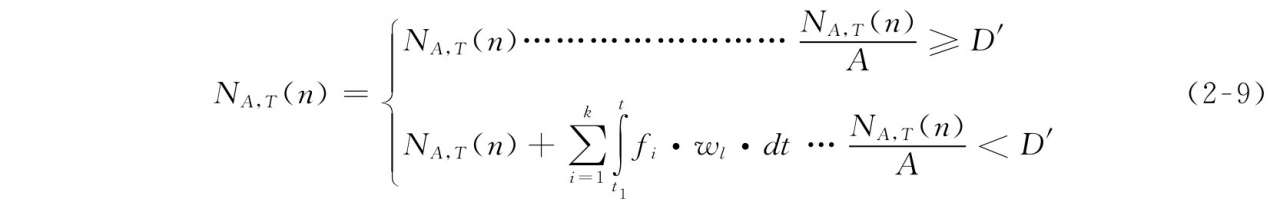
式中, N A, T ( n )为 t 1 < t ≤ T 时刻水平通道出口区域( A )在时刻 t ( n )的滞留人数,且 t ( n )∈[ t 1 , T ]。其他符号意义同前。
4.结果讨论
由于其他时间段出口处的滞留人数为线性增长关系,所以以( t 0 < t ≤ t 1 )时间段为研究重点进行分析,此阶段也为人群拥挤踩踏事故最可能发生的阶段。出口人群流动系数[ f ( D )]和出口宽度( W )都是影响出口滞留人数的重要参数,下面分别进行讨论。
基于人群流动系数与人群密度的经验关系,计算滞留人数随时间的变化情况,并设定三种不同的出口宽度( W 1 =2 m, W 2 =4 m, W 3 =8 m)分别进行计算如图2-36、图2-37和图2 - 38所示。
(1)出口宽度 W 1 =2 m 时滞留人数随时间变化关系。
由图2-36可以看出,对于2 m出口宽度来说,滞留人数随时间变化并不是简单的线性关系,并且随着时间的增长所有滞留曲线都是增加的,但是都有一个急剧增长的时刻,并且这个时刻的出现对于不同的人群流动系数与人群密度的关系是不同的。
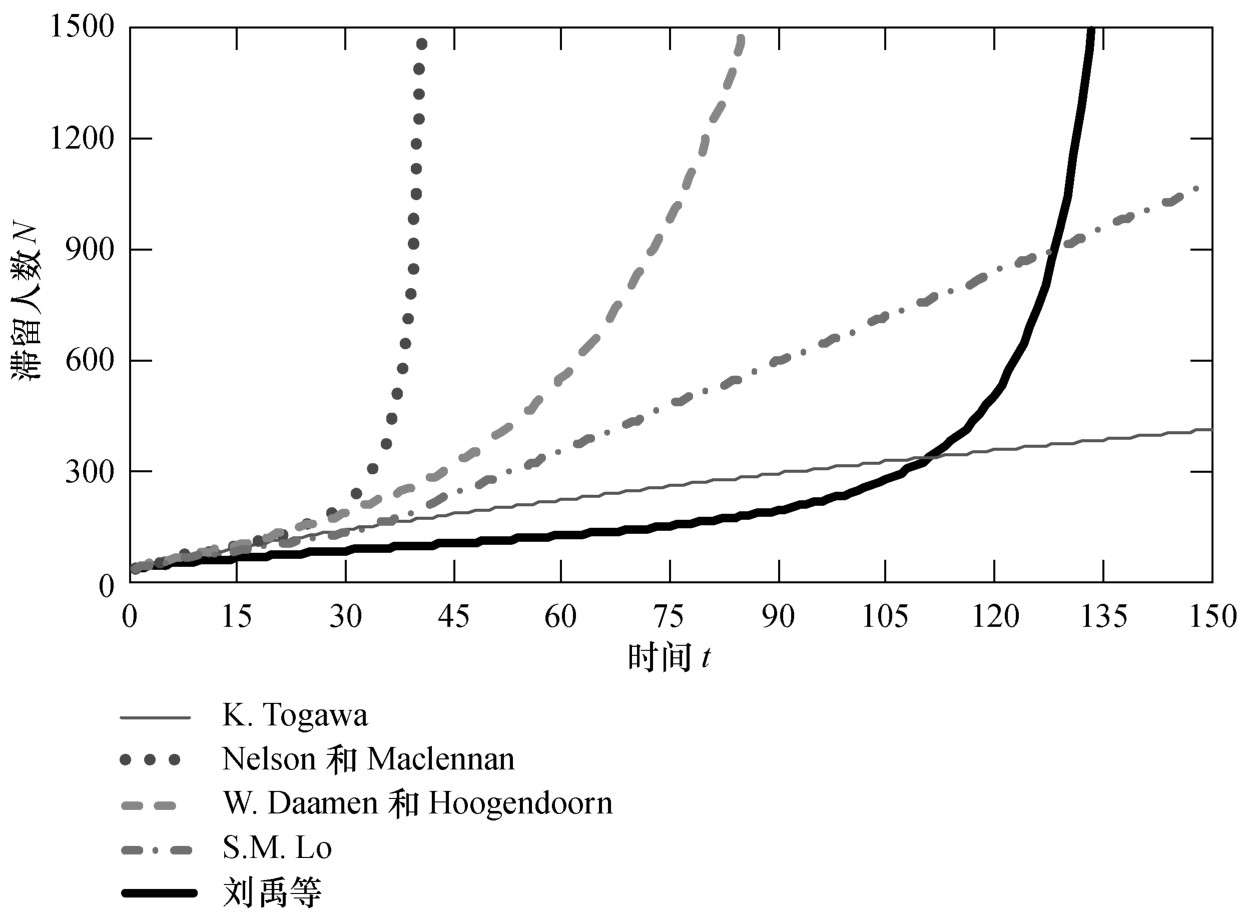
图2-36 出口宽度 W 1 =2 m时滞留人数随时间变化关系
(2)出口宽度 W 2 =4 m 时滞留人数随时间变化关系。
如图2 - 37所示,对于4 m出口宽度来说,出口处滞留人数随时间变化关系也不是线性增长的。基于W.Dammen和Hoogendoom, Nelson和Maclennan的人群流动系数与人群密度关系曲线推出的滞留人数曲线随着时间的增长,滞留人数增加,并且出现滞留人数急剧增长的时刻。而基于K.Togawa, S.M.Lo et al和刘禹等的人群流动系数与人群密度关系曲线推出滞留人数曲线几乎是一条直线,也就是说进入出口多少人,疏散出去多少人,出口处不会出现大量滞留人群。
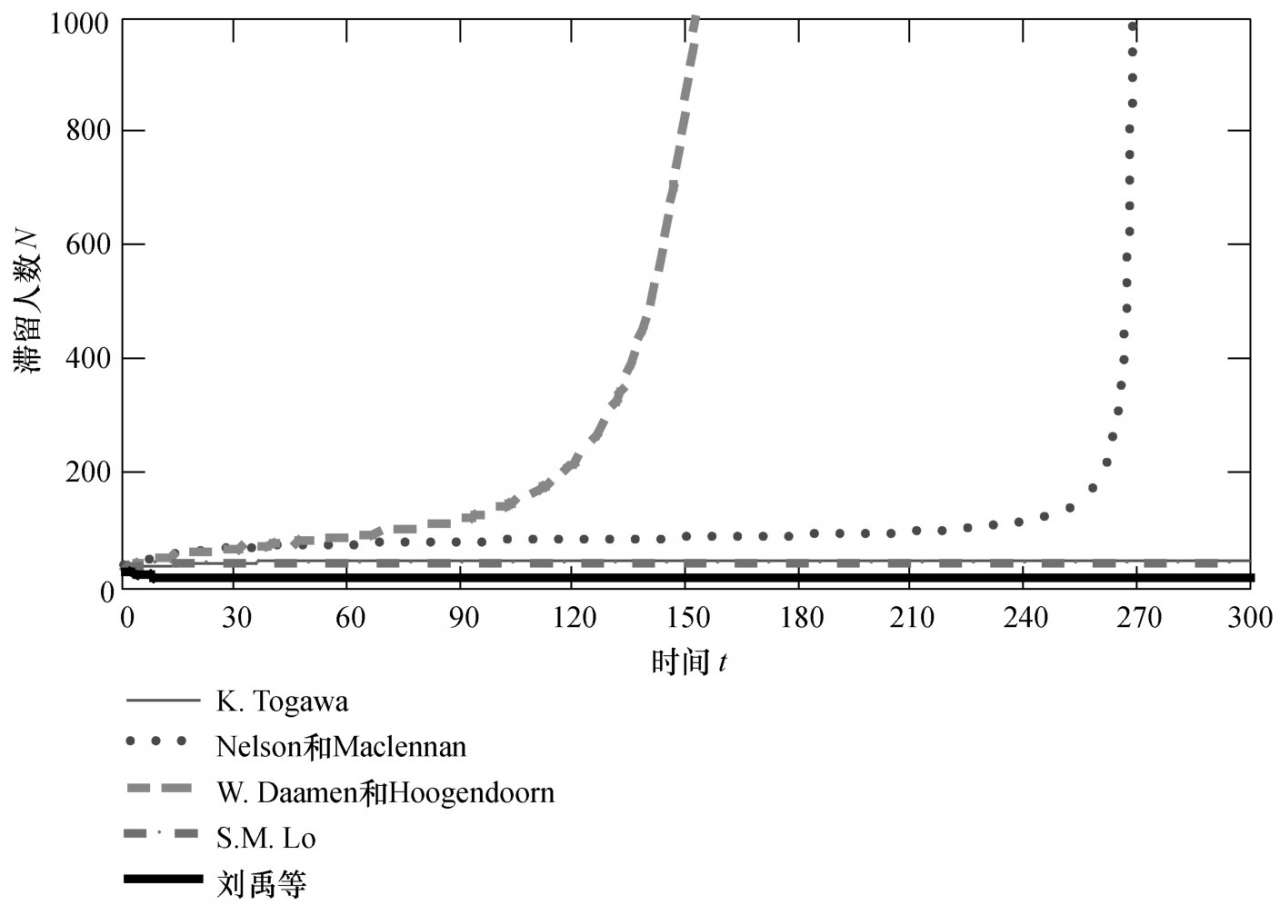
图2-37 出口宽度 W 2 =4 m时滞留人数随时间变化关系
(3)出口宽度 W 3 =8 m时滞留人数随时间变化关系。
如图2-38所示,当出口宽度为8 m时,滞留人数随时间变化都不是线性增长关系,而是随着时间的增长,滞留人数下降到一定值后并保持此值,也就是说对于8m宽的出口来说所有基于人群流动系数与人群密度关系曲线得到滞留人数几乎没有变化,也就是出口处不会出现滞留人群,也就不会出现人群拥挤踩踏事故发生,所以说出口宽度对于减少事故发生也很重要的。
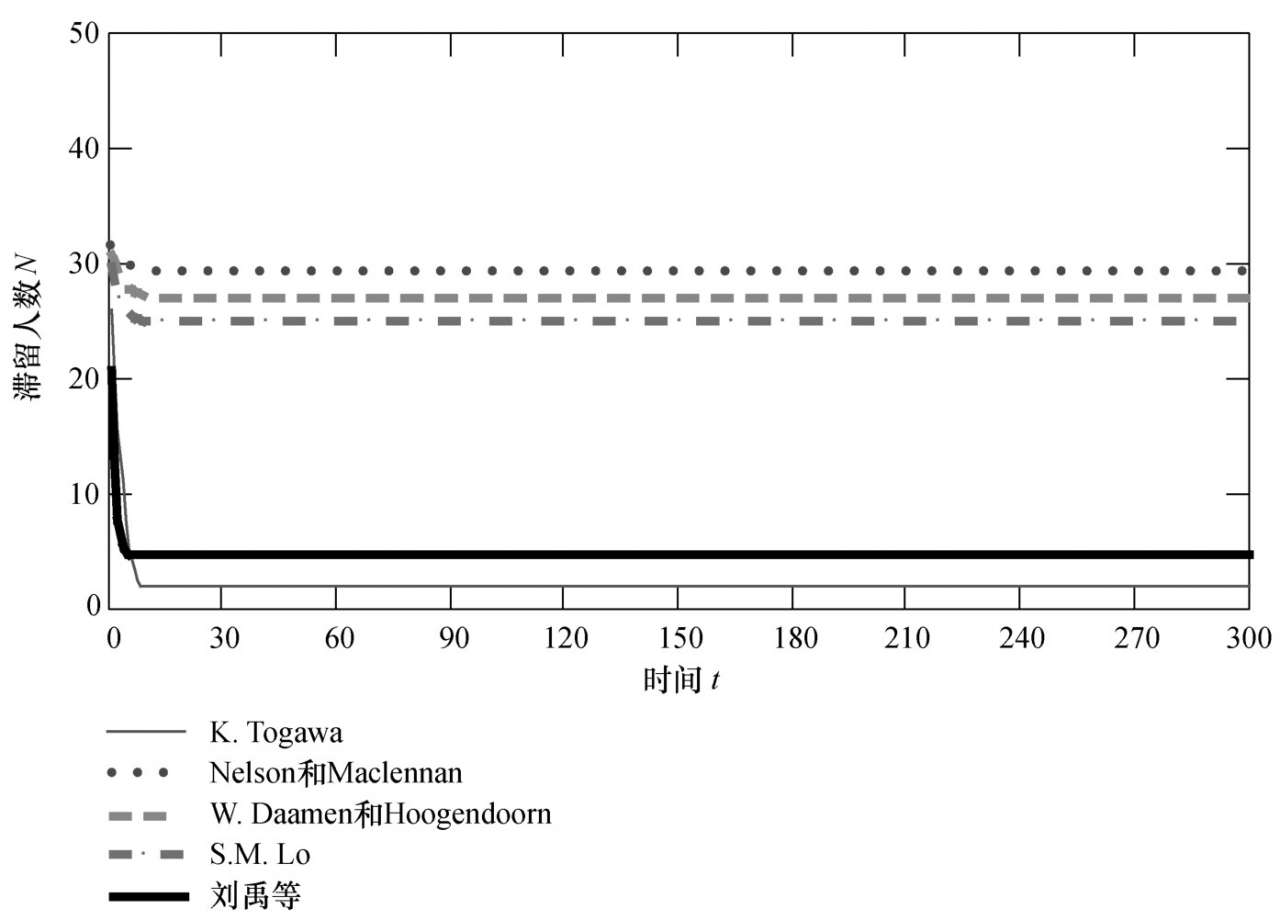
图2-38 出口宽度 W 3 =8 m时滞留人数随时间变化关系