
下载掌阅APP,畅读海量书库
立即打开




给定两条不等的直线,从较大的直线上截取一条直线等于较小的。
Given two unequal straight lines, to cut off from the greater a straight line equal to the less.
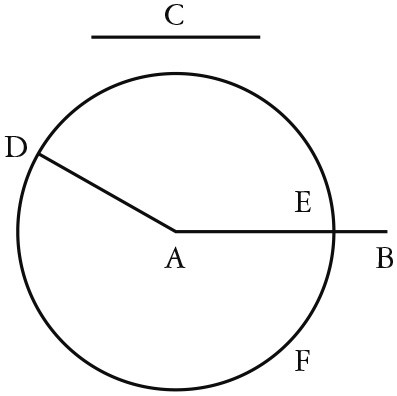
设AB、C是给定的两条不等的直线,且AB是其中较大的。
于是,要求从较大的AB上截取一条直线等于较小的C。
从点A作AD等于直线C;
[I. 2]
以A为圆心、AD为距离作圆DEF。
[公设3]
现在,由于点A是圆DEF的圆心,所以
AE等于AD。
[定义15]
又,C也等于AD。
因此,直线AE、C中的每一条都等于AD;
于是,AE也等于C。
[公理1]
这样便从给定的两条直线AB、C中较大的AB上截取了AE等于较小的C。
这就是所要作的。