命题22

由分别等于三条给定直线的三条直线作一个三角形，则任意两条直线之和必定大于另一条直线。

Out of three straight lines, which are equal to three given straight lines, to construct a triangle: thus it is necessary that two of the straight lines taken together in any manner should be greater than the remaining one.

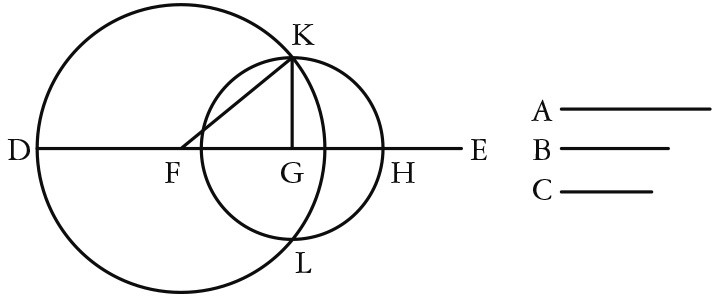
设三条给定直线是A、B、C，其中任意两条之和大于另一条，即

A、B之和大于C，

A、C之和大于B，

B、C之和大于A；

于是，要求由分别等于A、B、C的三条直线作一个三角形。

作一条直线DE，一端为D，但沿E的方向有无限长，

取DF等于A，FG等于B，GH等于C。

[I. 3]

以F为圆心、FD为距离作圆DKL；

又，以G为圆心、GH为距离作圆KLH；

连接KF、KG；

我说，三角形KFG就是由分别等于A、B、C的三条直线所作的三角形。

这是因为，由于点F是圆DKL的圆心，所以

FD等于FK。

但FD等于A；

因此，KF也等于A。

又，由于点G是圆LKH的圆心，所以

GH等于GK。

但GH等于C；

因此，KG也等于C。

而FG也等于B；因此，三条直线KF、FG、GK等于三条直线A、B、C。

这样便由分别等于三条给定直线A、B、C的三条直线KF、FG、GK作出了三角形KFG。

这就是所要作的。 1533EqKv7ijFXcMrJg/L70vosmmXq6LelOXUjXg/PfGcnfWeO3dHHef4hL7Jnzzk