下载掌阅APP，畅读海量书库
立即打开
在一直线上[从它的两个端点]作两条直线相交于一点，则不可能在该直线同侧[从它的两个端点]作另外两条直线相交于另一点，使得所作的两条直线分别等于前面两条直线，即分别等于与之有相同端点的直线。
Given two straight lines constructed on a straight line [from its extremities] and meeting in a point, there cannot be constructed on the same straight line [from its extremities], and on the same side of it, two other straight lines meeting in another point and equal to the former two respectively, namely each to that which has the same extremity with it.
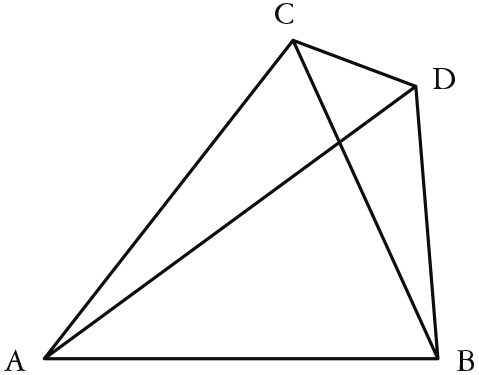
这是因为，如果可能，在直线AB上作两条直线AC、CB，它们交于点C，
在AB同侧作另外两条直线AD、DB相交于另一点D，且这两条直线分别等于前面两条直线，即与之有相同端点的直线，
于是，CA等于与之有相同端点A的DA，
且CB等于与之有相同端点B的DB；
连接CD。
于是，由于AC等于AD，所以
角ACD也等于角ADC；
[I. 5]
因此，角ADC大于角DCB，
因此，角CDB比角DCB更大。
又，由于CB等于DB，所以
角CDB也等于角DCB。
但已证明，角CDB比角DCB更大：
这是不可能的。
这就是所要证明的。