将下列循环小数化成分数 .

（1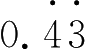） ； （2） .

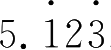思路分析 我们通过观察知道这两道题都是纯循环小数，也就是方法应该是相同的，只是循环节个数的多少不同，所以总结这个规律是很重要的 .在实际计算中，我们可以用移动循环节的方法化循环小数为分数 . 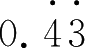的循环节是两位，便可以乘100，然后与原数做减法，便可以得到99× 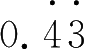=43，两边同时除以99，便能够把 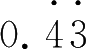化成分数了 .同样 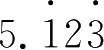的整数部分可以不考虑，而它的循环节是三位，便可以乘1000，然后按照刚才的方法便能够化成分数了 .

一个纯循环小数的小数部分化成分数，这个分数的分子是一个循环节表示的数，分母各位数字都是9，9的个数与循环节的位数相同，最后能约分的再约分 .

仿照上面的做法，还可以将混循环小数化成分数 .

例 将下列循环小数化成分数 .

（1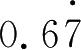） ；（2） .

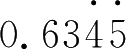思路分析 准备性训练中我们学习了把纯循环小数化成分数，而对于混循环小数怎样化成分数呢？这就需要同学开动脑筋，想一想，混循环小数与纯循环小数有什么区别呢？能不能把混循环小数先变成纯循环小数呢？所以第一步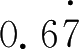： ×10=6 .7777……，第二步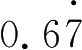： ×100=67 .777……，最后把两个算式做减法 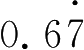×（100-10）=67-6，所以 = .

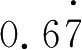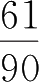而 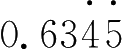与 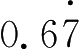的区别在于不循环的数位是两位，循环节是两位 .所以 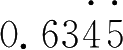×100=63 .4545……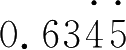， ×10000=6345 .4545……，然后按照刚才的方法计算 .

你能自己总结如何将混循环小数化成分数的方法吗？

将一个混循环小数化成分数，分子是小数点后面第一个数字到第一个循环节的末位数字组成的数与不循环部分数字所组成的数的差，分母的前几位是9，后几位为0，其中9的个数等于循环节的位数，0的个数等于不循环部分的位数 .

1. 把下列分数化为小数 .（观察分母的质因数与小数位数的关系）

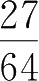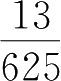（1） ；（2） ；（3） .

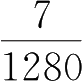2. 把下列分数化为小数 .（观察循环节有什么异同）

， ， ， ， ， .

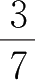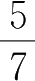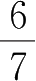3. 把下列小数化为分数 .

（1） 0.24；（2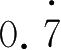） ； （3） .

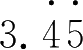4. 将下列小数化成分数 .

（1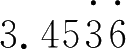） ；（2） .

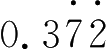5. 计算下列各题 .

（1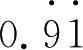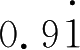） - ； （2） + + +…+ .

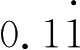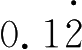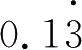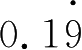1. 假定m是一个正整数，d是1~9中的一个数字，已知 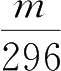= 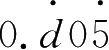，求m .

2. 把整数部分是0、循环节由3个数字组成的纯循环小数化成最简真分数后，分母是一个两位数，这样的最简真分数有多少个？ S8Tbss9hIlX+QGkwzULIxHSegQRblO1B1oSlDbBwwb4Ath3nQzbFnVdcvUgDjzA3