





[ 题 ]著名物理学家爱因斯坦生病的时候,为了逗他开心,他的一个做传记作者的朋友莫希柯夫斯基给他出了下面这道题(图2-3):
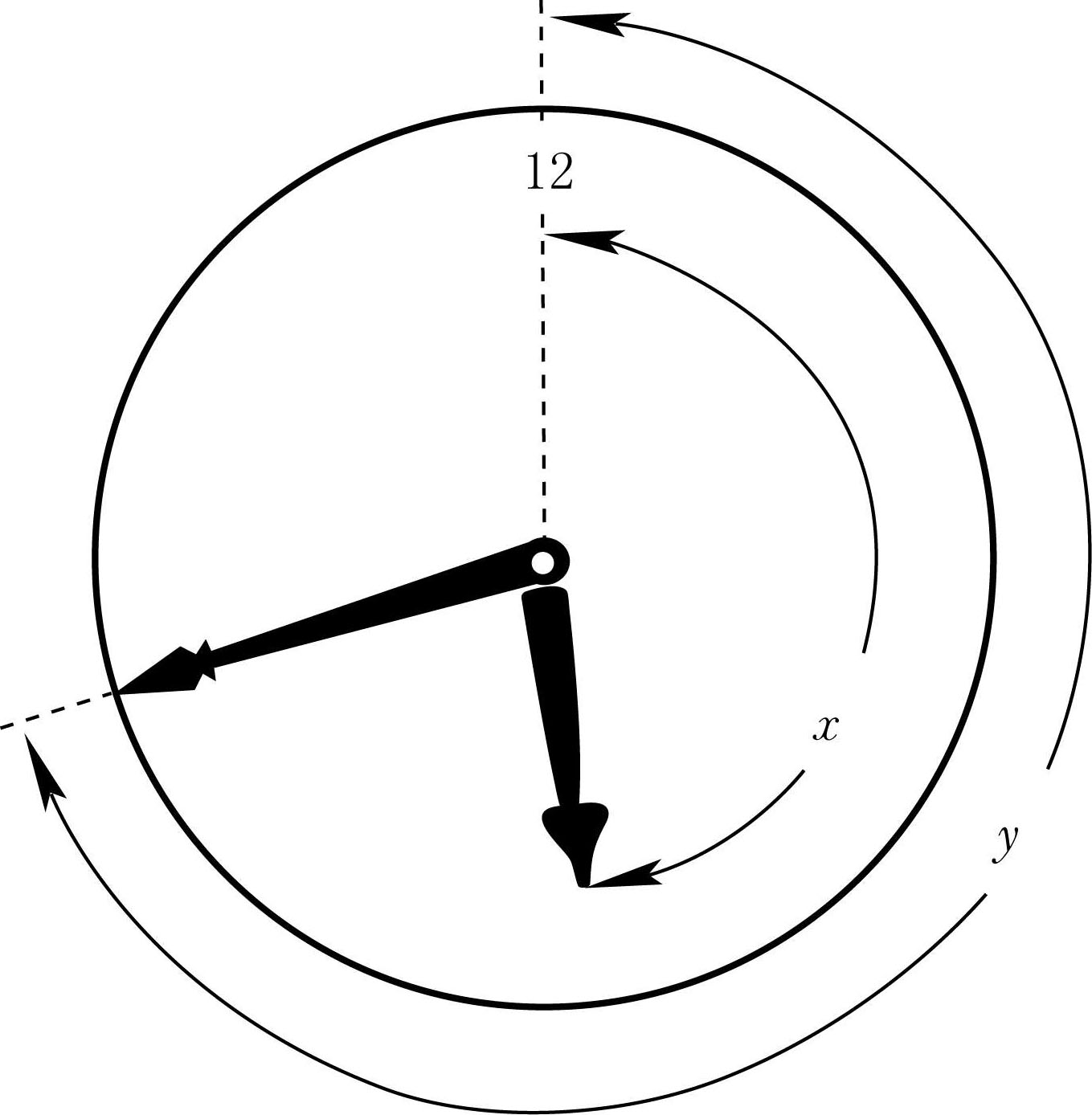
图2-3
“假设表针的初始位置是在12点。在这个位置,如果把较长的分针和较短的时针对调一下,它们所指示的时间还是存在的。但是在很多别的时候,把两针对调之后所出现的结果就不合理了,比如6点的时候,我们如果把两针对调,出现的结果就是正常情况下不可能出现的:这个时候时针指向12而分针指向6。这种位置关系是不合理的。由此可以引出这样一个问题:表针处在什么位置的时候,即使两针对调,所得的新位置显示的仍然是可能存在的时间?”
爱因斯坦回答道:“非常好,这个问题十分有趣而且也不是特别简单,非常适合躺在病床上的人。只是对于我来说,它恐怕消磨不了多少时间,我已经快解出来了。”
爱因斯坦从床上坐起来,用几笔在纸上勾出了一个草图来表示问题的条件。他解这个问题所用的时间甚至不超过莫希柯夫斯基叙述这个问题所用的时间……
那么,他是怎样解答这道题的呢?
[ 解 ]首先,我们不妨把表盘圆周分成相等的60份,并以每份为单位,来计算表针从12开始所走的距离。
假设在时针从12起走了
x
个刻度,分针走了
y
个刻度之后,达到了符合题目要求的位置。时针走过60个刻度需要12个小时,这也就是说,时针每小时能走5个刻度,那么它走过
x
个刻度所需的时间就是
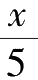 小时。换句话说,就是在表走到12点之后 ,又过了
小时。换句话说,就是在表走到12点之后 ,又过了
 小时。每个小时有60分钟,所以分针走过
y
个刻度所用的时间就是
小时。每个小时有60分钟,所以分针走过
y
个刻度所用的时间就是
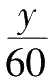 小时。也就是说,分针是在
小时。也就是说,分针是在
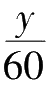 小时之前经过数字12的。换言之,两根指针在12的地方重合之后又过了(
小时之前经过数字12的。换言之,两根指针在12的地方重合之后又过了(
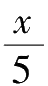 -
-
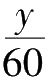 )小时。由于(
)小时。由于(
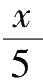 -
-
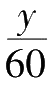 )这个数所表示的是12点之后又过去了几个整小时,所以这个数是从0到11之间的一个整数。
)这个数所表示的是12点之后又过去了几个整小时,所以这个数是从0到11之间的一个整数。
当两根指针的位置调换了之后,我们可以用同样的方法求出从12点到调换后的时间为
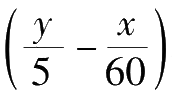 小时。这个数也是个从0 到1 1 之间的整数。
小时。这个数也是个从0 到1 1 之间的整数。
根据这些,我们可以列出联立方程:
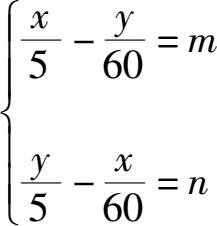
由这个联立方程我们可以解出:
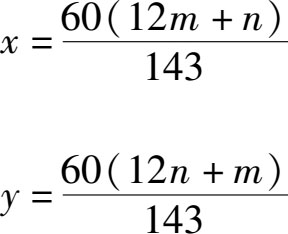
在这个方程中, m 和 n 都可以任取从0到11之间的整数。所以,要想确定全部所求表针的位置,只要把从0到11之间的全部整数都代入到上述的方程中就可以了。由于 m 可以取的12个数中任何一个都可以与 n 可以取的12个数中的任意一个组合,所以,很多人会觉得这道题应该有12×12=144个解。实际上,不是这样。由于 m 、 n 均为0时与 m 、 n 均为11时表针所处的都是同一个位置,也就是12点。所以,这道题其实只有143个解。
我们不讨论所有可能出现的情况,只找两个例子来看一看。
第一例:
当 m =1, n =1时,
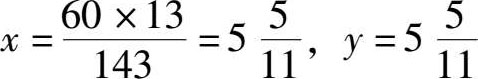
对应的时刻也就是1点
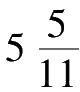 分,此时时针和分针是重合在一起的;时针和分针重合在一起的时候,它们当然可以彼此对调。
分,此时时针和分针是重合在一起的;时针和分针重合在一起的时候,它们当然可以彼此对调。
第二例:
当 m =8, n =5时,
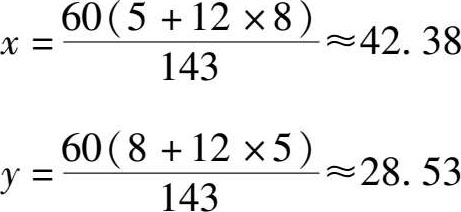
这时所指的时刻应该分别是8点28.53分和5点42.38分。
当我们把表盘的圆周平均分成143份时,所得到的平分点就是这道题的解。表针指向这样的点时,把时针和分针对调,它们所指的时间仍然存在。而当表针指向这143个点之外的那些点时,如果对调时针和分针,它们所指的时间将会是不合理的。