[ 题 ]我们上面所讲的题目就是从牛顿关于牛的数量的原题衍生出来的。这个题目并不是牛顿自己想出来的，而是人们在长期的数学学习过程中创造出来的。现在，让我们来看看牛顿的原题。

有三个面积分别为 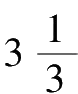公顷、10公顷和24公顷的牧场。三个牧场上的草都长得一样密，生长速度也一样快。第一个牧场如果饲养12头牛的话，可以吃4个星期；第二个牧场如果饲养21头牛的话，可以吃9个星期。问：在第三个牧场上饲养多少头牛可以恰好吃18个星期？

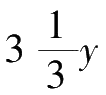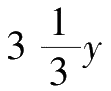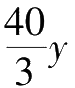[ 解 ]跟前面一样要解这道题我们需要设一个辅助的未知数，用来表示一个星期里面1公顷牧场上长出的草占原来的草的总量的比重。现在，我们设这个比重为 y 。则第一个牧场上一个星期所长出的草是1公顷牧场上原有草的总量的 倍。那么，4星期的时间第一个牧场上长出的草就是1公顷牧场上原有草的总量的 ×4= 倍。这就相当于把原来的第一个牧场的面积增加到了

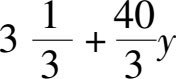
公顷。也就是说，牛吃掉的是面积为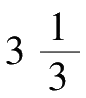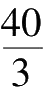（ + y ）公顷的牧场上的草。12头牛用4 个星期可以把草吃完，也就是说，每个星期牛可以吃占总草量的 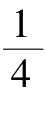的牧草。那么一，头牛一星期吃掉的草就是总草量的 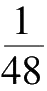，据此我们可以列出下列等式：

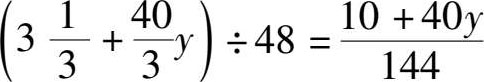
也就是说一头牛每个星期所吃的草是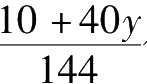， 公顷的牧场上的草量。

同理，我们也可以从已知的条件中推算第二个牧场上一头牛一个星期可以吃掉的草的面积：

1个星期里，1公顷草地长出的草为 y 。

那么9个星期里，10公顷草地上长出的草的总量就是90 y 。

所以21头牛在9个星期的时间内吃掉的其实是（10+90 y ）公顷的牧场上草的总量。

那么每头牛每个星期吃掉的草的面积是

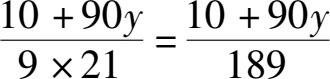
公顷。由于每头牛每个星期吃掉的草的量是相等的，所以我们可以据此列出等式：

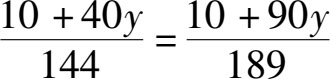
解这个方程可以得出： y = 。

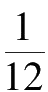下面，让我们来求一下可以让1头牛吃一个星期的牧场的面积是多少：

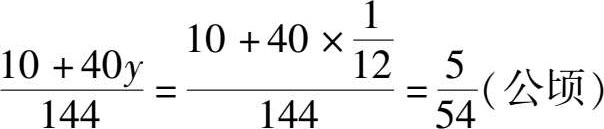
最后，我们假设第三个牧场上牛的头数为 x ,然后列出方程：

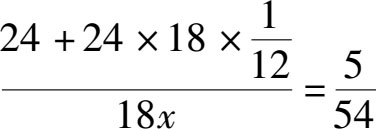
解这个方程可以得出： x =36。也就是说，在第三个牧场上饲养36头牛可以恰好吃18个星期。 I0e/EpWPM/j7ZkG6gN2tiLkSVPPfBGKItt6VYJa7XTCNXmVt4Z+wxqg/5HzLwMwo