[ 题 ]牛顿在阐述理论的时候，总是喜欢结合实例来说明。他认为，在学习科学的过程中，做题比死记硬背那些规则更有用。在牛顿所列举的众多实例当中，有一个牛吃草的问题非常经典，我们下面要讲的这道题就是在牛顿问题的基础上演化而来的。

在契诃夫的小说《家庭教师》中有一个非常搞笑的故事情节。家庭教师给他的学生出了这样一道题：

牧场上的草长得一样密，生长的速度也一样快。已知，要吃完牧场上的草，70头牛需要用24天，而30头牛则需要用60天。那么，如果要在96天内把牧场上的草吃完，需要多少头牛？

学生接到这个题目以后，就找了两个成年的亲戚来帮他做。做了很久也没有结果，他们感觉非常困惑：

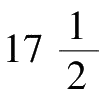其中一个亲戚认为这是一个很简单的问题，甚至完全用不着思考，答案当然是70的 （即24/96），也就是 头牛。这显然不对，让我们再看看下一个条件：30头牛用60天可以把草吃完，多少头牛用96天能吃完这些草？结果是：30× 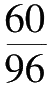=18 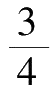头，显然也不对。还有题目本身也有一，些让人困惑的地方，既然70头牛吃完草需要用24天，那么30头牛要吃完它只要用56天就行了，但是题目中却说要60天。

另一个亲戚说道：“你没有把草一直在生长这个条件考虑进去吧？”

这句话非常对。草是不停生长的，如果不把这个因素考虑进去，不仅这个题目解不出来，我们甚至会怀疑题目本身的正确性，觉得题中所给出的条件都是自相矛盾的。

那么到底应该怎样解答这道题目呢？

[ 解 ]在这里，我们需要用一个辅助的未知数来表示每天长出的草在牧场上草的总量中所占的比重。设每天长出的草为 y ,那么24天就能长出24 y ;假设牧场上草的总量是1,那么24天里70头牛吃掉的草的总量就是（1+24 y ）。那么这群牛一天吃掉的草的量就是：

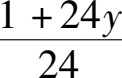
由此可以看出一头牛一天吃掉的草的量就是：

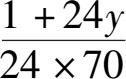
同理，由于30头牛用60天可以把牧场上的草吃完，所以，一头牛一天吃掉的草的量就是：

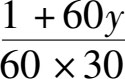
由于每头牛每天吃掉的草的量是一样的。我们可以列出下面的方程：

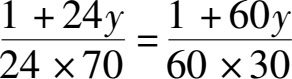
解这个方程可以得出：

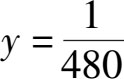
根据这个已经算出了的每天长出的草占牧场上草的总量的比重 y ,再利用下面的方程，我们很容易就能求出一头牛一天吃掉的草的量占原来牧场上草的总量的比重：

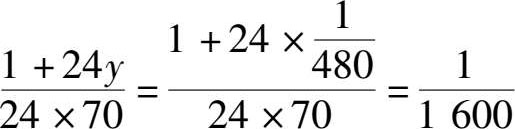
我们设所求的牛的数量是 x ,列出最后解这道题的方程：

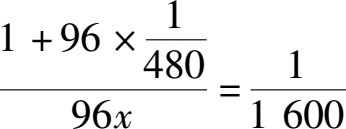
解这个方程，可得：

x =20

因此，如果要在96天内把牧场上的草吃完，就需要20头牛。 R0FoNpun9SiLoQeWXUFwTYXzHGcw+p4LJqyL94Mb0vnV6tsk/ezdXxdHg2KXWXU0