[ 题 ]下面，我们对上面这道题目做一点延伸：

当有四个2时，我们要怎么摆，才能得出最大的数字呢？

[ 解 ]四个2一共能产生8种摆法，即

2 222,222 ² ,22 ²² ,2 ²²²

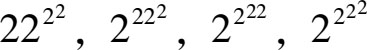
这8种摆法中，哪个得到的数值最大呢？

先看第一行中用两层摆法所得到的这几个数。

在第一行中，第一个数2 222显然是最小的。

如果想更加方便地比较后面两个数——222 ² 和22 ²² 的大小，我们可以把22 ²² 换一种写法：

22 ²² =22 ^2×11 =（22 ² ） ¹¹ =484 ¹¹

对于484 ¹¹ 来说，无论是底数，还是指数，都比222 ² 大。因此22 ²² 要比222 ² 大。

现在我们再拿22 ²² 去与第一行的最后一个数2 ²²² 比较一下大小。

由于

32 ²² =（2 ⁵ ） ²² =2 ¹¹⁰

222>110,所以2 ²²² 自然要大于32 ²² 。而32 ²² 又比22 ²² 大，所以，2 ²²² 要比22 ²² 大。

经过上面的比较可知，第一行中，最大的数字是2 ²²² 。

下面让我们从剩下的5个数中找出最大的数。用第一行的最大数2 ²²² 和第二行的4个数进行比较：

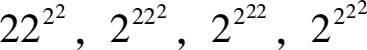
首先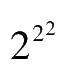， =16,16比222小得多，所以最后一个数字可以排除掉。其次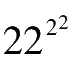， 相当于22 ⁴ ,22 ⁴ 小于32 ⁴ ,所以22 ⁴ 比2 ²⁰ 要小，因此22 ⁴ 比2 ²²² 小得多，也可以排除掉。这样一来，就只剩3个数字了。而所剩下的这3个数又都是以2为底的乘方，我们只需要比较它们的指数就可以了。这3个数的指数分别为

222,484,2 ²² （2 ^10×2 ×2 ² ≈10 ⁶ ×4）

其中，2 ²² 显然是最大的。因此 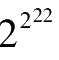是用四个2所能写出的最大的数。

在不使用对数表的情况下，我们可以利用下面的近似等式来求出2 ^{2 22} 的近似值。

由于

2 ¹⁰ ≈10 ³

所以

2 ²² =2 ²⁰ ×2 ² ≈4×10 ⁶

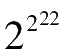≈2 ^{4000 000} >10 ^{1 200 000}

也就是说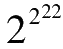， 是一个100万位以上的庞大数字。 Zxr0mqbZX/y0E3g4ACZfzNGn6dUMipK0R4q8Q3kuqlFQ/+w88m7k93BOv/+i73l4