下载掌阅APP，畅读海量书库
立即打开
[ 题 ]假如将一块石头扔到水里，原本平静的水面上就会产生许多个圆圈，这个现象在生活中非常常见，如图2-21所示。如果让你解释这个现象，你肯定会说这很容易，石头激起的波浪以石头为圆心，以相同的速度向四周扩散，所形成的波纹是一个大圆，所有的浪点都和波浪中心距离相等。
前面我们说的是向平静的水面扔石头，如果换成是流动的水面会产生什么现象呢，石头所激起的波浪还会是圆形的吗？还是会扭曲成别的形状比如椭圆形呢？
图2-21 水面上的圆形波纹
粗略想一下，你可能会觉得石头产生的圆形波浪会随着水流的方向而扩展，而且顺流的速度比逆流的速度快一些，所以看起来应该是伸长的封闭曲线，怎样也无法形成圆形。不过你的这个猜想和实际情况可不一样，即使是水流十分湍急的河流，将石头扔进去也会形成圆形，这是为什么呢？
[ 解 ]如果水面是静止不动的，那么波纹一定是圆形的，这是毋庸置疑的，那么在流动的水中会发生什么变化呢？
如图2-22（a）所示，圆形的波纹被河水的流动所吸引，每一个点都被吸引到图上箭头表示的方向，而且所有的点移动的距离都是相等的，它们移动的速度也是一样的，且沿着相互平行的方向移动，这样的移动自然不会改变图形的形状。如图2-22（b）所示，带有新的点1′，2′，3′，4′的四边形取代了原来带有点1,2,3,4的四边形，对应的点1到了点1′的位置，点2移到了点2′的位置，所以两个四边形是完全一样的。如果我们在圆周上取更多的点，那么就会得到全等的多边形，当我们取无数的点也就相当于整个圆周，这样平行移动后，可以证明这两个圆形是全等的。这也就是为什么即使把石头扔到流动的水中形成的波纹仍然是圆形的原因了。不过，如果圆圈波纹不会从中心向四方扩散的话，湖泊的水面上圆圈不会产生移动，而河水上面的圆形移动的速度是和河流的速度相等的。
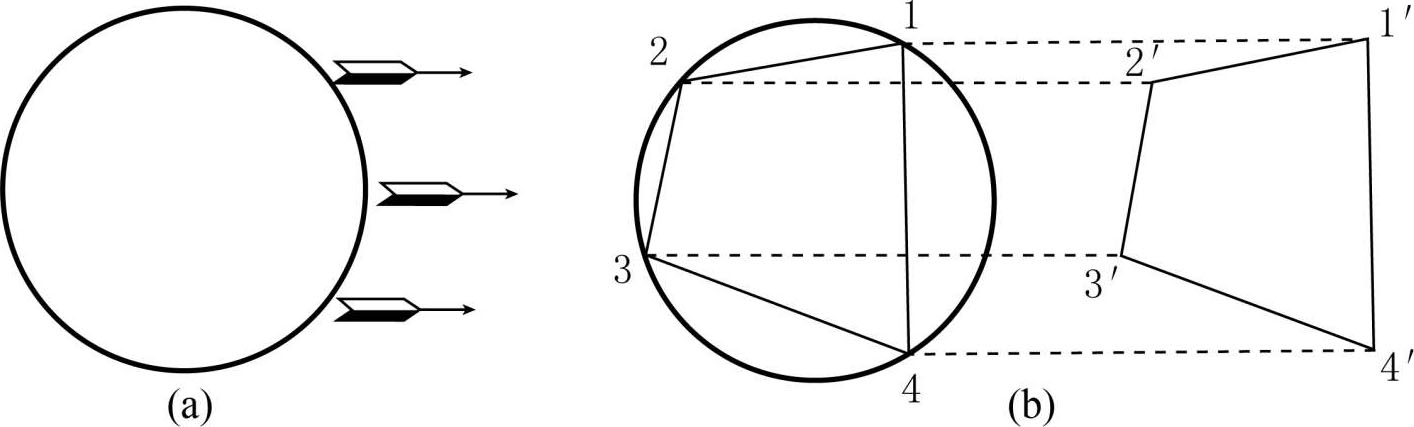
图2-22 水流并不会改变波纹的形状
所以，无论水面是平静的还是流动的，波纹的形状都是圆形。