





这种似乎万能的公式的确存在,而且并非仅适用于上述所提的圆柱、圆锥和圆台,也可以普遍适用于所有种类的棱柱体、棱锥体、棱台体以及球体。以下就是被称作“辛普森公式”的著名万能公式:
V
=
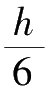 (
b
1
+4
b
2
+
b
3
)
(
b
1
+4
b
2
+
b
3
)
其中, h 是立体的高度; b 1是下底面积; b 2是中部截面面积; b 3是上底面积。
[ 题 ]试着证明利用上述公式确实能计算出以下七类几何体的体积:棱柱、棱锥、棱台、圆柱、圆锥、圆台、球体。
[ 解 ]将上述公式分别用以计算以上七种几何体体积,即可验证。
对于棱柱和圆柱[图1-16(a)],得出:
V
=
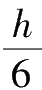 (
b
1
+4
b
2
+
b
3
)=
b
1
h
(
b
1
+4
b
2
+
b
3
)=
b
1
h
对于棱锥和圆锥[图1-16(b)],得出:
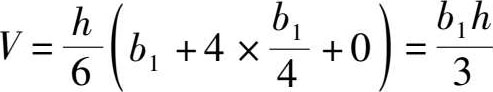
对于圆台[图1-16(c)],得出:
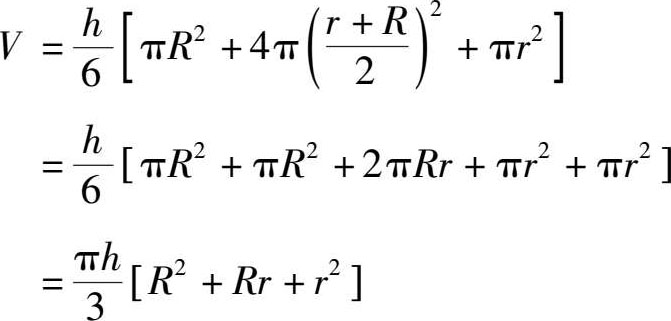
对于棱台的,也可用相似的证明方法。
最后,对于球体[图1-16(d)],得出:
V
=
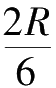 (0+4
π
R
2
+0)=
(0+4
π
R
2
+0)=
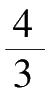 π
R
3
π
R
3
[ 题 ]万能公式还有一个有趣的特性:它还适用于平面图形的面积计算,如平行四边形、梯形、三角形。公式是一样的,只要把公式当中的字母含义改换如下即可:
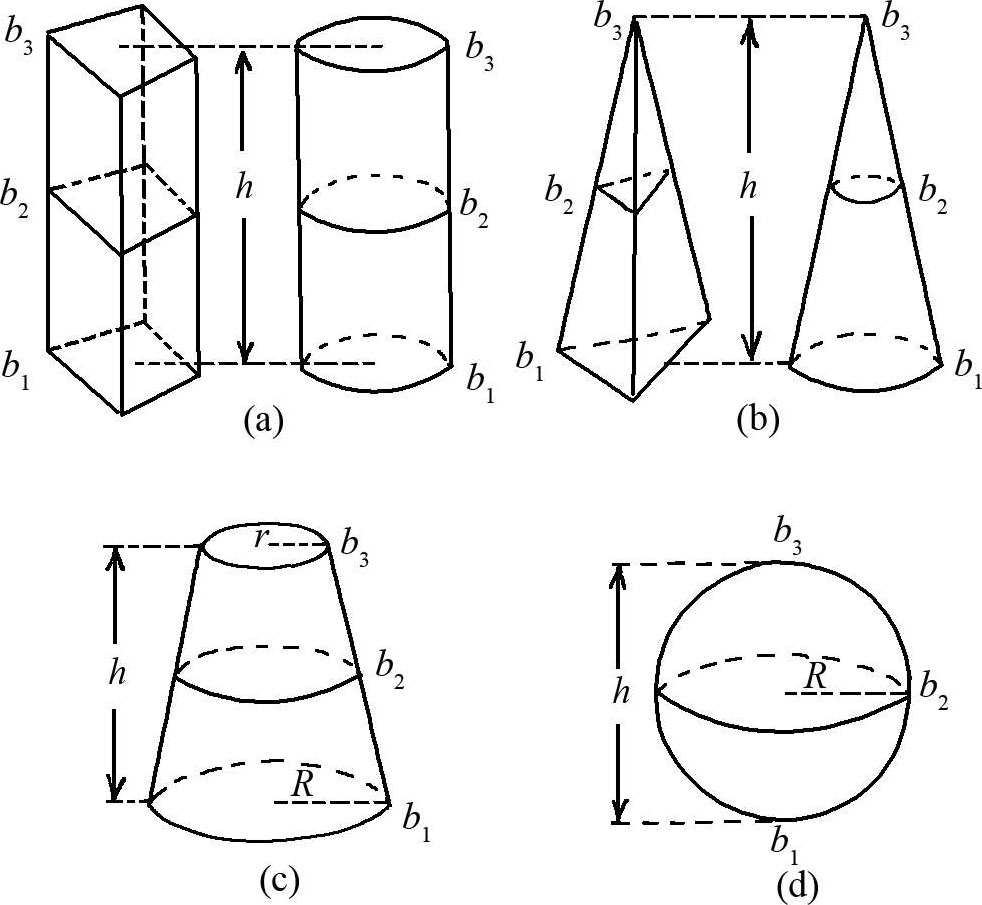
图1-16 万能公式适用的几种几何体
其中, h 是图形的高度; b 1是下底长度; b 2是中间线长度; b 3是上底长度。
如何证明呢?
[ 解 ]把万能公式应用到平行四边形(包括正方形和矩形)[图1-17(a)]面积计算中:
S
=
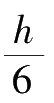 (
b
1
+4
b
2
+
b
3
)=
b
1
h
(
b
1
+4
b
2
+
b
3
)=
b
1
h
梯形[图1-17(b)]的面积为:
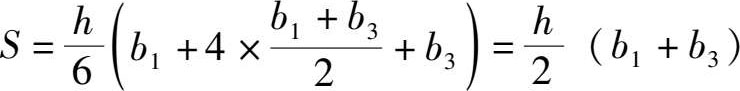
三角形[图1-17(c)]的面积为:
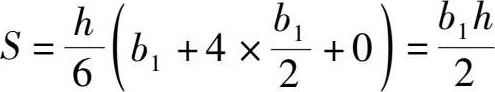
由此可见,“万能公式”的“万能”二字当之无愧。
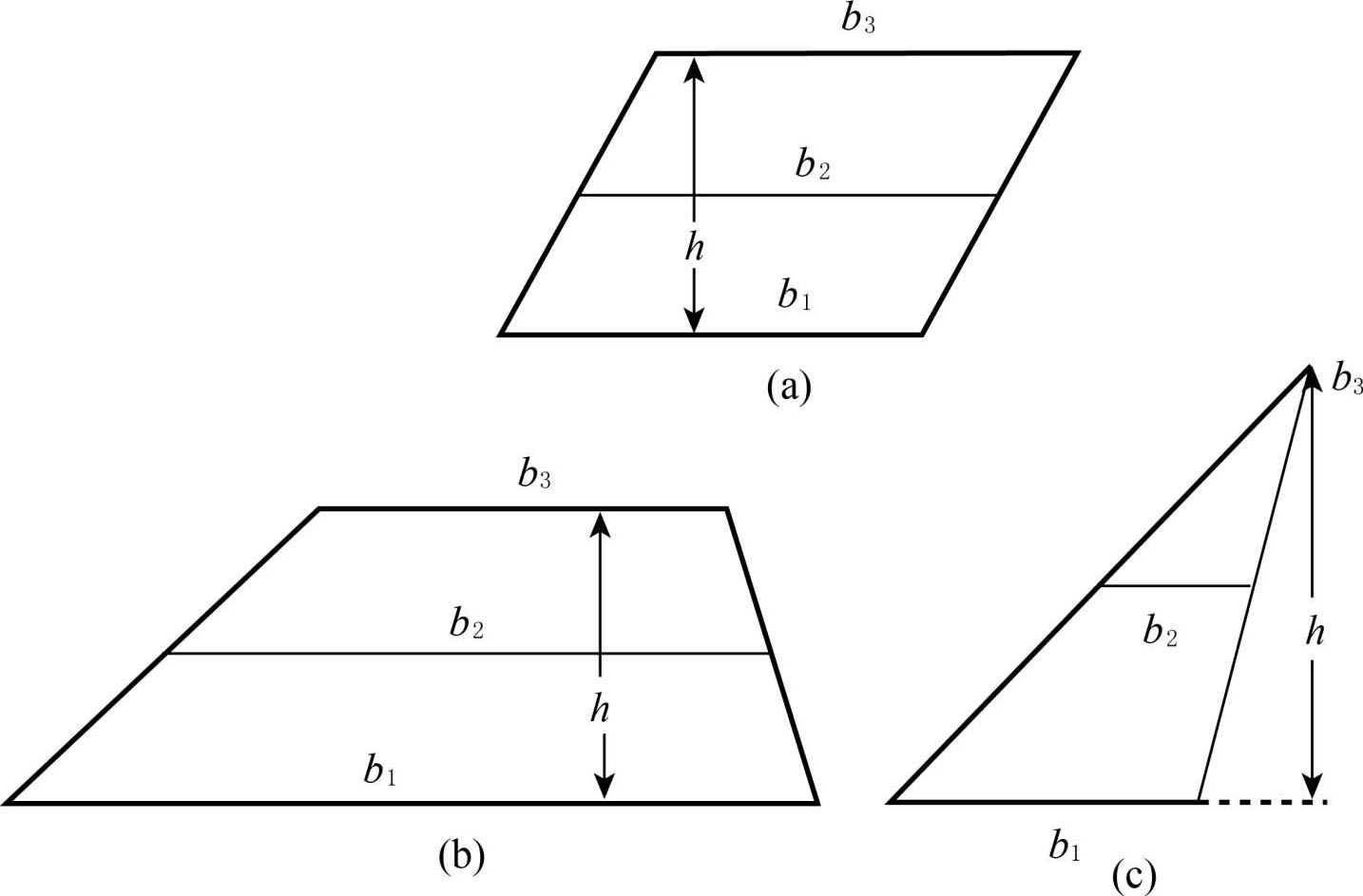
图1-17 适合用万能公式的图形