





[ 题 ]借助镜子也可以测量树木的高度,你知道吗?如图1-14所示,如果把一面镜子平放在被测树木附近的 C 点上,使 C 点和大树保持一定的距离,然后观测者从 C 点退后到 D 点,使得在 D 点时可以从镜中看到树顶 A 点。那么这时候树高 AB 是观测者身高 ED 的多少倍?从镜子到树根的距离 BC 是从镜子到观测者距离 CD 的多少倍?请说出原因。
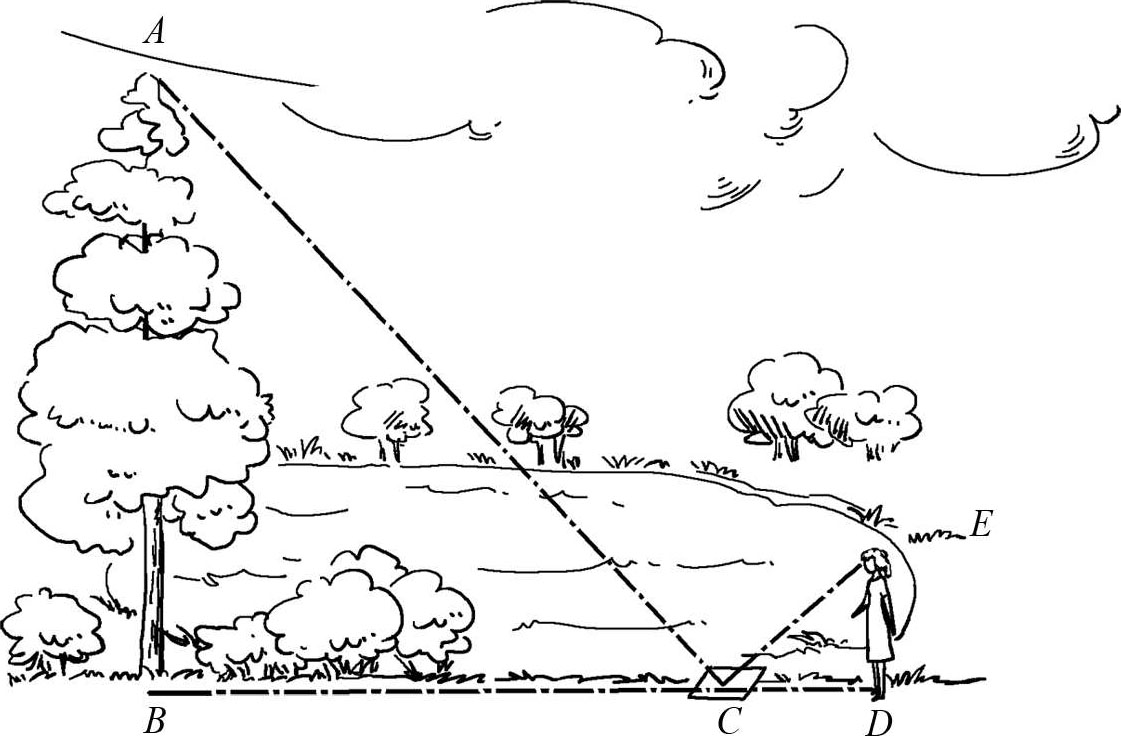
图1-14 使用镜子测量树的高度
[ 解 ]可以用光的反射定律来证明。树顶 A (图1-15)倒映在 A′ 点上,所以 AB = A′B 。又因为三角形 BCA′ 和三角形 DCE 相似,可得:
A ′ B ∶ ED = BC ∶ CD
又因为 A′B 与 AB 相等,因此比值可求。
镜子测高法与光的反射定律相关,在任何天气条件下都可以使用,十分简便易行。不过也存在局限,就是只能测量独立的树木,在密林当中测量树木不宜使用。
[ 题 ]如果我们因为某种原因无法靠近树木,用镜子测高法能否测出树木高度呢?如果可以,如何使用?
[ 解 ]可以测出。通过两次运用上面的方法即可。首先把镜子放在两个地方进行测量,利用两个相似三角形的比例关系可推出,树高应为人眼距地面的距离乘以镜子两次测量位置的距离与观测者和镜子距离之差的比。
其实这道题是600年前的经典古题,中世纪数学家安东尼·德·可莫雷纳曾在其著作《土地的实用测量》(1400年)中对其作过详细研究。
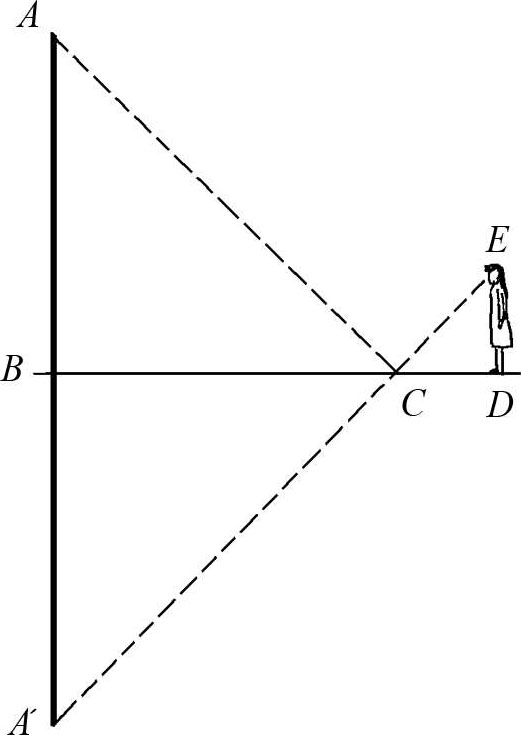
图1-15用镜子测高的几何示意图
我们已经讨论了很多关于测量树高的问题,最后我给读者留一道与之相关的计算题,供大家思考。