





著名科幻作家儒勒·凡尔纳因为他的一系列科幻作品吸引了世人的关注,他小说中的一些设想在今天已经实现。不过,小说《从地球到月球》中提出的向月球发射一个载人特大号炮弹式车厢的构想究竟能不能实现呢?虽然凡尔纳在小说中已经提出了自己的解决方案,但这个方案仍然仍有许多疑点。
首先,我们应该探讨一下向月球发射一枚炮弹让它永远不落回地球,是否具有理论上的可行性。我们都知道由于万有引力的关系,水平射出的炮弹的飞行路线会发生弯曲,迟早会落到地面上。尽管地球是个球体,它的表面是一个曲平面,然而炮弹飞行路线的弯曲度要远远大于地面的曲率,假设我们能够使炮弹的路线的曲率变得和地球表面相同,那么这枚炮弹只会沿着地球的圆周同心曲线飞行,并且由于万有引力的作用无法摆脱这个曲线,从而变成像人造卫星一样的东西。
那是不是有可能使炮弹的飞行路线曲率小于地球表面的曲率呢?首先它必须具备同样的速度。图2-11是地球一部分的剖面图,假设我们在山上的 A 点放置一门大炮,在不存在万有引力的情况下,炮弹水平射出1秒它就可以到达目的地 B 点。然而事实上,一秒钟后它仅仅能到达低于 B 点5米的 C 点处。我们假设我们的炮弹下落5米后恰好是它应该到达的高度,也就是说是没有引力的情况下到达的地方。
那我们先算出 AB 线段的长度,得出炮弹在1秒钟水平方向要走过的路程,从而求出为了实现我们的目的炮弹需要的初速度。在三角形 AOB 中, AB 的长度很容易就得出了, AO 为地球的半径约6 370000米, CO = OA , BC =5米,所以 OB =6 370 005米,根据勾股定理, AB 2 =6 370 005 2 -6 370 000 2 。
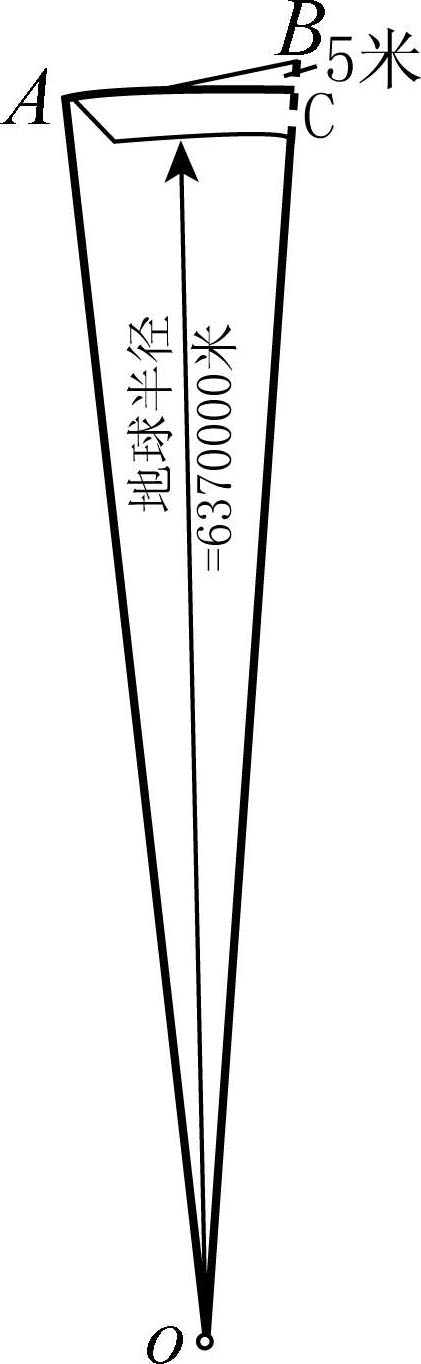
图2-11 计算永远不会落回地球的炮弹的速度
经过计算,我们得知,AB大约等于8千米。
所以,即使在有万有引力存在的情况下,如果没有影响快速运动的炮弹的空气,只要炮弹是以8千米/秒的速度射出,它就会像地球的卫星一样围绕着地球运转。
当大炮射出的炮弹速度大于8千米/秒的时候,它将围绕地球做椭圆运动。根据天体力学,从炮口飞出的炮弹初速度越大,椭圆就越长。经计算,当初速度达到11.2千米/秒时,炮弹就能够永远地离开地球飞到宇宙中去(图2-12)。
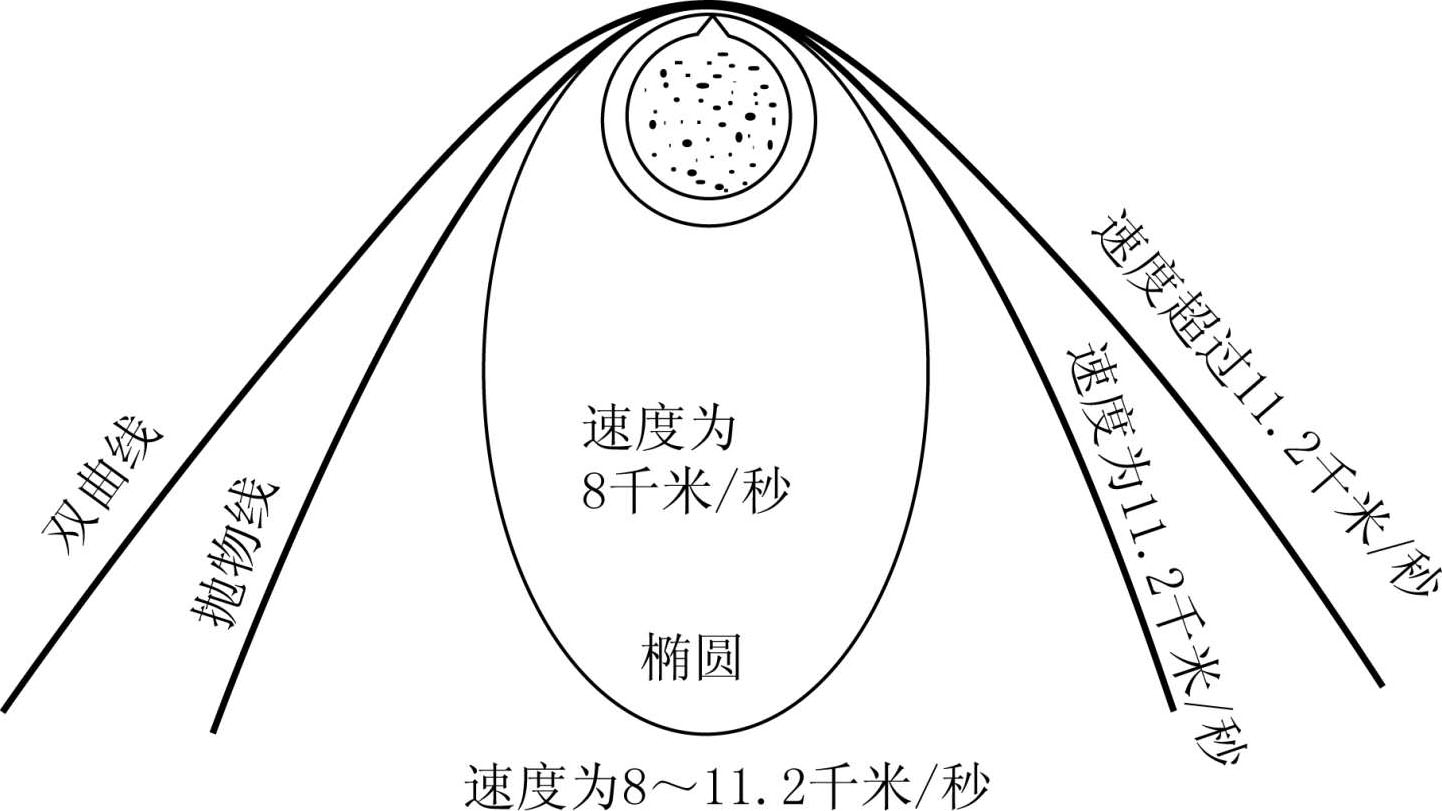
图2-12 以8千米/秒以上的速度射出去的炮弹的命运
所以从理论上来说,如果大气不阻碍炮弹运动,只要炮弹达到足够大的速度,它就能够飞到月球上去。因为现实中大气阻碍运动,形成这种高速度是一种极大的困难。