子集与推出关系

上海市行知中学 张建国

一、教学目标

1.理解集合间具有包含关系的充要条件是这些集合的性质具有推出关系.

2.掌握用集合的包含关系进行推理的方法.

3.经历用集合知识解决逻辑推理问题的过程.

4.养成独立思考的习惯,提高分析问题、解决问题的能力,锻炼抽象概括能力和逻辑思维能力.

二、教学重点

理解子集和推出关系的本质,学会用集合的包含关系进行推理的方法.

三、教学难点

掌握用集合的包含关系进行推理的方法.

四、教学方法

学导式教学方法.

五、教学流程设计

六、教学过程

(一)课前预习

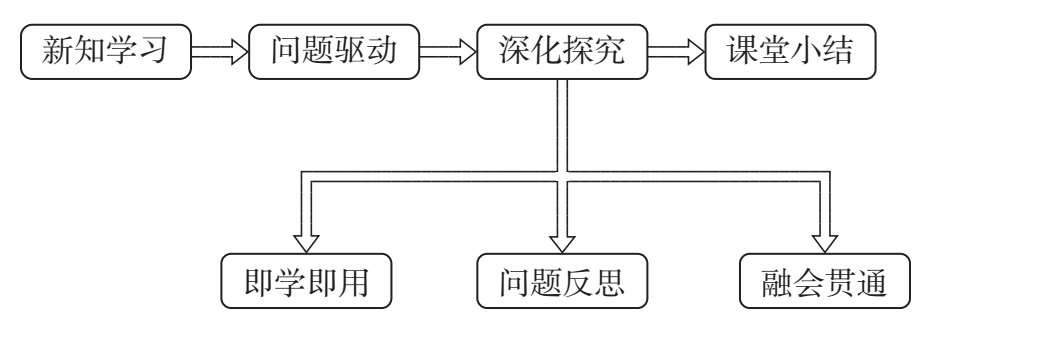
说明: 1.课前发下学案,学生在温故知新中预习新知,为本节课的学习打好基础.

根据课前学案,与学生们共同理解“集合间具有包含关系的充要条件是这些集合中元素的公共属性的性质具有推出关系”.

(二)新课讲授

1.建立子集与推出关系的联系

2.师生讨论后得出结论.

设 A ={ a | a 具有性质 α }, B ={ b | b 具有性质 β },则 A B 与 α β 等价.

上述等价性可以理解为:

2.及时巩固

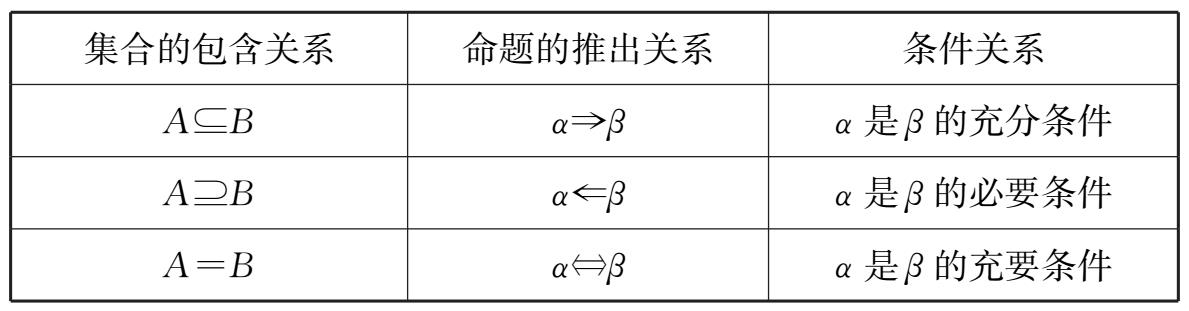
3.借助题目使学生进一步理解子集与推出关系的联系.

例1 判断命题 α : x =1, β : x ² =1之间的推出关系.

分析:记 A ={ x | x =1}, B ={ x | x ² =1}.

因为 A ={1}, B ={1,-1},所以 A B ,从而 α β .

例2 判断集合 A ={ n | n =2 k , k ∈Z}, B ={ n | n 的个位数是2, n ∈Z}之间的关系.

分析:设命题 α : n =2 k ( k ∈Z),命题 β : n 是个位数是2的整数.

因为命题 α : n =2 k ( k ∈Z),即 n 是偶数,

所以 β α ,从而 B A .

3.加深感受

4.例3、例4进一步加深学生体会“利用子集的包含关系”解释“命题的推出关系”.

例3 利用子集和推出关系,判断下列命题的真假.

(1)如果 a >2,那么 a ≥2.( )

(2)如果 ab ≠0,那么 a ≠0或 b ≠0.( )

分析:关于(1).

学生: (易错点)假!

教师: 用子集与推出关系可以解释.

分析:关于(2).

学生: ab ≠0 a ≠0且 b ≠0之后,可以用子集和推出关系解释.

教师: 正确.

例4 已知非空集合 A 、 B ,则命题 α : x ∈ A ∩ B 是命题 β : x ∈ A ∪ B 的( ).

(A)充分条件 (B)必要条件

(C)充要条件 (D)既非充分也非必要条件

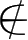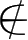思考:若本题改为“已知非空集合 A 、 B ,则命题 α : x A ∩ B 是命题 β : x A ∪ B 的______条件.

学生: “ 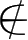”会导致无从下手,思维混乱.

教师: 由子集与推出关系可知,直接从推出角度思考问题比较困难时,可以从集合角度研究!

说明:在判断“命题的推出关系”出现困难时,我们可以借助于“子集的包含关系”的帮助,抓住它们的内在联系,是我们解题的关键.

4.灵活应用

5.通过学生讨论,教师做适当指引,得出结论.

例5 设 α :1≤x≤3, β : m +1≤x≤ 2 m +4, m ∈R, α 是 β 的充分条件,求 m 的取值范围.

学生: 设 A ={ x |1≤x≤3}, B ={ x | m +1≤ x ≤2 m +4}.

因为 α 是 β 的充分条件,所以 A B .

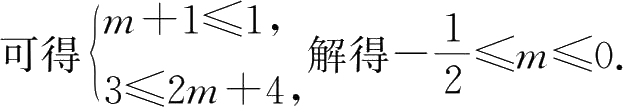
教师: 若 α 是 β 的必要条件则如何?(此处学生易忽略 β 为空集的可能性)

(三)课堂反馈

6.视学生的实际情况再决定教学内容.

根据课堂所发的学案,对教学情况进行检测和评价.

(四)类比深化

7.利用学案辅助,由学生自主完成.

根据本节课所学内容,类比以下结论:

设 A ={ a | a 具有性质 α }, B ={ b | b 具有性质 β },则

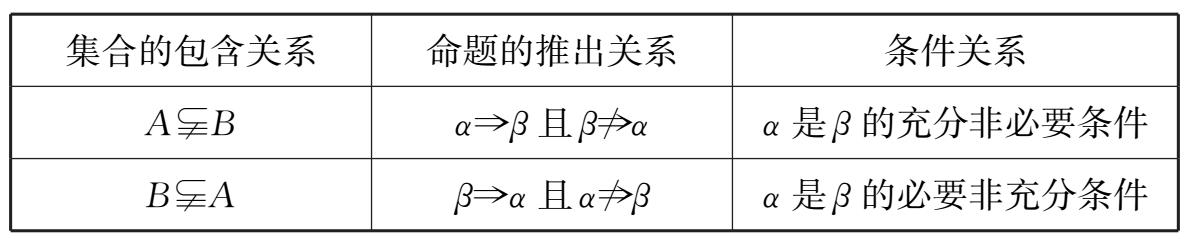
思考:在例5中,若 α 是 β 的充分非必要条件,则 m 的取值范围是多少?

七、教学设计说明

子集和推出关系主要探讨集合的包含关系与命题的推出关系之间的联系,在之前已经学习了集合的有关内容、四种命题形式和充分必要条件之后继续学习,将集合与命题加以沟通,融为一体,有助于学生更深刻地领会子集概念和命题关系,提高综合运用的能力.

本节内容的理论性较强,不建议学生死记硬背,需要从本质上理解、领悟从而灵活运用.所以本节课的教学设计要注意以下几点:

1.怎么提出这个课题而又不觉得突兀?本课从复习集合与命题的相关知识引出集合与命题练习的探讨.然后以实例进行巩固,目的在于让学生真正理解子集和推出关系.(见附录1)

2.将引例与主要知识以列表的形式呈现.学习理论性较强的知识,学生经常会出现困难,因此,把知识以列表的形式呈现,有助于记忆和理解.

3.以学生多思考、多交流为中心,促进学生主动学习.在教学的各个环节中,以学生为主体,引导学生动脑思考,鼓励学生提出问题、寻找联系、发现结论、尝试运用.

4.融入数学史的学习.借子集与推出关系向学生们介绍集合论的创始人康托尔,让学生觉得数学并没有那么枯燥.

八、教学反思

本节课的内容比较抽象,学生理解略显吃力,对某些题目的处理可以再细致一些,例如“已知非空集合 A , A ,则命题 α : x 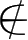A ∩ A 是命题 β : x 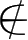A ∪ B 的______条件.”在学生思考之后,教师点评时如果能运用互为逆否命题的思考方法,会更有利于学生的理解.

另外,本节课学生若做好预习工作会更加理想,因此教师可以事先设计预习方案,有助于课堂效率的提高.

课堂评价见附录2.

九、专家点评

很多高中学生在学到命题这一节的时候都有这样的疑惑:为什么命题与集合是编写在一个章节的?本节内容给出了很好的诠释.在学习的过程中,我们应该注意知识与知识之间并不是孤立的,它们之间往往有着密切的联系.本节课建立起了“集合”与“命题”的内在联系,对于优化和提升学生的思维品质有着极大的帮助,可以让学生非常真切地感受到数学的和谐与统一之美,同时也激发了学生学习数学的兴趣,提高学生分析解决问题的能力. IO/Arvp4EBeAotiKCn4writIRTl5z0EL064qJszA+PSZXDGSHlsqchTf0+hNks4/