




为何斯莫林和罗韦利会受爱因斯坦影响,被科学思想的革命所吸引,其原因不难理解。在他们听老师讲课、勤奋地读书,以及解答教科书上的经典习题时,他们的视野被打开了,看到了一系列非凡的可能性。
时间和空间在我们大多数人看来再平常不过,但斯莫林和罗韦利却对之提出了非常基本的问题,来探讨它们的本质——我们的物理现实的结构。虽然我们已经对时空的表象那么熟悉了,但爱因斯坦向我们证明,关于时空本质的答案并 不是 显而易见的。他告诉我们,我们可以推翻权威、克服偏见,追寻更加深刻的真理。他在年仅26岁时就走上了这条革命之路。虽然爱因斯坦对物理学的贡献在科学史上无人可比,但他的工作显然还没有完成,还差最后一步。
爱因斯坦在《狭义与广义相对论浅说》附录五的开头写道:“牛顿物理学的特征在于,它给空间和时间赋予了独立而真实的存在,和物质一样。”
 在爱因斯坦诞生前两百年,英国机械哲学家艾萨克·牛顿于17世纪构建的这种“经典”物理学体系要求空间和时间的结构是绝对的。绝对的时空观非常符合我们的日常经验,以至于如果你完全没有接触过相对论,你会不假思索地视绝对时空观为理所当然。
在爱因斯坦诞生前两百年,英国机械哲学家艾萨克·牛顿于17世纪构建的这种“经典”物理学体系要求空间和时间的结构是绝对的。绝对的时空观非常符合我们的日常经验,以至于如果你完全没有接触过相对论,你会不假思索地视绝对时空观为理所当然。
但出于哲学方面的理由(我们之后会看到,这些理由也是十分实际的),我们应该完全抛弃绝对时空的观念。
在绝对时空观里,绝对的空间形成了某种容器,容器之中,有一种神秘的宇宙节拍器标记着绝对的时间。在这样一个容器里,作用力对物体施加作用,事情不断发生。如果我们把宇宙中所有的物质都清除掉,我们就不得不相信空的容器会留下,而节拍器仍然在宇宙中不断地滴答运转。这就意味着,宇宙中还有东西。
但剩下的到底是什么呢?根据逻辑,一切事物都存在于宇宙中,宇宙的定义就是如此。但绝对时空观暗示,宇宙本身即存在于这个容器中。如果沿着这个逻辑再推演一下,我们可以想象在宇宙外面有一个高高在上的点,从那里可以俯瞰整个宇宙——宛如上帝在俯瞰他创造的一切事物。
当然,想到这儿我们可以耸耸肩,认为抛开哲学(以及神学)上的意义之后,绝对时空观至少看起来是与我们的日常经验一致的。我们把东西放在哪儿,就能在哪儿找到它;我们上下班总是沿着同一条道路行走;我们的每一天总是从早晨开始。这些难道不都是我们物理现实的绝对性的体现吗?
但即使是这些日常现象,也并不是绝对的。只要稍微想一想,你就会发现,在表象之下,我们看到的物体仅仅是在互相靠近或者远离而已,改变的只是其相对彼此而言的位置。这就是相对运动,在我们的时空中,我们在原则上只能通过物体之间的相对关系定义物体的运动。牛顿也不得不承认,在我们普通人的日常生活中,确实只能如此。
因此,我们会设想使用坐标系(对于三维空间,我们使用三个两两垂直的坐标轴,分别标记为 x 、 y 、 z ),通过一个物体在某个时刻处于哪个位置,下一时刻又处于哪个位置来更精确地描述事物。这个方法好多了,或者说,看起来科学多了。
但不要高兴得过早,因为我们必须承认,这类坐标系的选取完全是任意的。
测量地球上的位置时,我们会使用另一套坐标系,它被称为经纬度,是由地球的形状和大小定义的。我们测量时间的系统的基础是地球绕着太阳的运动,以及地球绕地轴的自转。这些系统看起来十分“自然”,但它们只对于我们地球生物而言是自然的,而且我们不能否认它们的选取实际上是十分任意的。像 x 、 y 、 z 或者经纬度这样的坐标系被称为参考系,我们可以在其中定位物体,并观察事情的发生。
我们还可以更进一步思考。任何做匀速直线运动的物体看起来都是从一个地方移动到另一个地方,但“移动”到底是什么意思呢?是说物体从这个地方以特定的速度移动到了那个地方,还是说物体其实是静止的,只是“那个地方”以同样的速度移动到了“这个地方”?
J.R.R.托尔金的著作《魔戒》的粉丝可能会想起皮平与甘道夫一同坐在捷影
 上匆忙赶往米那斯提力斯的经历:“皮平慢慢进入了梦乡,他有种奇怪的感觉:自己和甘道夫端坐在一匹奔马的雕像上,像石头般一动也不动,与此同时,世界在狂风呼号中从他脚下滚滚而去。”
上匆忙赶往米那斯提力斯的经历:“皮平慢慢进入了梦乡,他有种奇怪的感觉:自己和甘道夫端坐在一匹奔马的雕像上,像石头般一动也不动,与此同时,世界在狂风呼号中从他脚下滚滚而去。”


在这种匀速运动的例子中,从原理上就没有任何观测或测量手段能告诉我们到底是哪一方在运动。当然,简单的逻辑推断就能告诉我们,上面那段话说的是捷影在静止的中洲上狂奔,但不可否认的是,我们永远无法 证明 这一点。
这类匀速运动完全是相对的,物理学家在所谓的“惯性”参考系的背景下定义它。从刚刚的描述中我们知道,宇宙中根本不存在绝对的坐标系,也没有绝对(或最终)的惯性参考系,因此也就没有绝对运动。所谓的“上帝视角”,根本不存在。
如果某个概念在原理上与观测或实验无关,也就是说,我们无法积累关于它的实证经验,我们就通常认为它是“形而上学”(metaphysics,字面意思是“超越物理学”)的。那么,为什么牛顿会坚持使用绝对时空观这种我们永远无法直接体验的、形而上学的系统呢?因为只有做出绝对时空的假设,他才能用相对简单的公式表示 运动定律 ——众所周知,牛顿的运动定律是极为成功的。
牛顿运动定律的成功给人们带来了极大的慰藉,也使得人们倾向于忽略这套理论描述所需要的有时极强的假设和前提条件。然而,在19世纪末,一股新的经验主义哲学力量正在生长壮大,逐渐获得了科学上的话语权。该哲学流派要求完全摒弃形而上学的构造,将其从科学中彻底清除。
经验主义哲学的势力正在积蓄,而在此时苏格兰物理学家詹姆斯·克拉克·麦克斯韦(James Clerk Maxwell)打乱了他们的计划。
当时,种种实验证据表明,电现象与磁现象之间有着千丝万缕的联系。因此,从1855年开始,麦克斯韦在长达10年的时间里发表了一系列论文,将这两种不同但密切关联的现象分别用 电场 和 磁场 加以描述。我们可以用“力线”来形象地描绘这类场,它们通常从正电荷出发通往负电荷,或是从北极出发通往南极(见图1)。这类场绝不只是丰富的想象力的产物:当你试图把两块磁铁的北极对在一起时,你就能切实 感受到 它的存在。
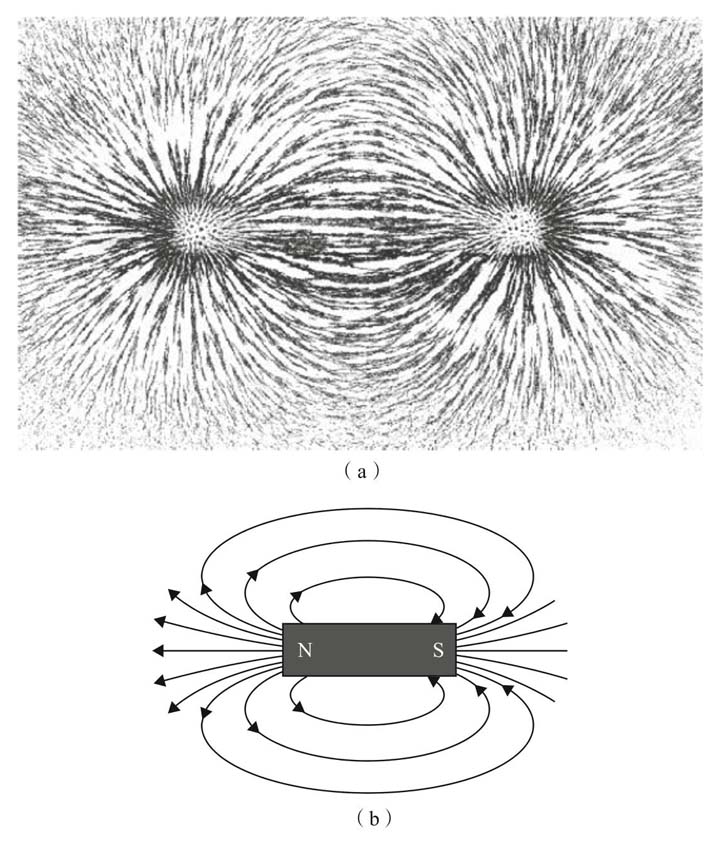
图1

但这就已经不仅是物体在三维空间、一维时间里的运动了。麦克斯韦的电磁场方程描述了一种完全不同的新的物理学。在空空如也的空间里,我们也能感受到磁铁周围的磁场(我们可以轻易地证实,磁场可以存在于真空中,它并不需要空气来传递)。实际上,对麦克斯韦方程组做一些简单的变形,就能清晰地描述 波 的运动了。
这与日益增多的支持光的波动说的证据完全相符,它说明光就是电磁辐射的一种形式。麦克斯韦方程组还可以进一步用于计算真空中电磁波传播的速度,结果证明就是真空中的光速,我们用符号 c 表示它。
但在科学史上(在生活中也是一样),某一瞬间的明确清晰,往往意味着其他方面会出现混乱。电磁辐射的本质现在看起来清晰明了、毋庸置疑,但另一方面,物理学家不得不承认,电磁波必须存在于某种介质中。
如果你把一块石头扔进湖里,你就会看见它在水面上产生了波纹。这种水波正是“介质中的波”的一个典型例子,就水波而言,介质就是水。没有哪种波不需要介质,电磁波 也必须 存在于某种介质中。麦克斯韦本人确信,电磁波一定是在“以太”中运动的——以太是一种假想中的稀薄的物质,它是电磁波的介质,充满整个空间。
所有的物理学实验和观测证据都表明,如果以太确实存在,它不可能参与可观测物体的运动。以太必须是静止的。如果以太是静止的,从定义上讲它就是绝对的:它充满了绝对空间所形成的容器。这样一来,静态的以太就定义了根本意义上的惯性参考系。
嗯……
问题来了,这里存在一些微妙的不同。牛顿定律要求空间是绝对的,只能静静地在那里当一个背景。从定义上讲,我们永远不可能体验到这种绝对空间。但现在麦克斯韦的理论告诉我们,我们的周围真的有一个绝对空间,其间 充满了以太 。这与牛顿的绝对时空观截然不同。
我们不妨这样想一下:如果地球在静态的以太中绕着地轴自转,我们应该就能在地球表面感受到一股“以太风”(实际上叫“以太曳引”,不过结果是一样的)。我们认为以太十分稀薄,因此我们也许并不能像感受风一样感受到它。但介质有另外一种可以测量的效应:假如一道声波沿着一股很强的风向我们传来,我们测量到的它的速度就会比无风时同样的声波快。因此可以预期,如果光顺着以太风的方向射向我们,我们测量到的光速就应该比逆着以太风的方向射向我们的光速快。如果以太是静态的,就意味着不同方向的光速是不一样的。
就算不同方向上的光速有差异,应该也会很小,但19世纪末的光学技术足以测量到这种差异了。但1887年,美国物理学家阿尔伯特·迈克耳孙(Albert Michelson)和爱德华·莫雷(Edward Morley)没能在实验中测量到光速的差异。在他们的实验精度范围内,光速是恒常不变的,与方向无关。他们的实验结果显示,根本就不存在静态的以太这种东西。
这类谜团把看似遥远的科学理论问题带到了我们的生活中。牛顿运动定律要求空间和时间是绝对的,而我们永远不可能体验到绝对时空,也无法获得任何关于它的经验证据。麦克斯韦的电磁波理论要求存在充满整个空间的静态以太,以容纳电磁波,但实验告诉我们并不存在这种东西。我们该怎么办呢?
就在这个时候,一位在伯尔尼的瑞士专利局工作的年轻的“三级技术专家”站了出来。1905年,爱因斯坦根据自己的物理学和经验主义哲学判断,要解决这个问题,我们需要一个新的理论,从完全实际的角度出发,让“观测者”位于舞台的中心。这里的“观测者”并不一定是人类。爱因斯坦引入这一概念的用意是,为了正确理解物理学,我们必须接受这样一个事实:每个人或者每个物体眼中的物理学过程,都只是他们(或它们)正在观察或用尺子和时间测量出来的物理学过程而已。
当然,这种观察者的默认设定属于牛顿理论。但牛顿理论又是通过假设观察者位于整个现实的外部而建立的,换言之,观察者是站在“上帝视角”看着万物运转的。爱因斯坦则把观察者带回了舞台上,令其处于自己观察的现实之中。
爱因斯坦首先陈述了两条基本原理。第一条被他称为“ 相对性原理 ”,其内容是:以不同(但恒定)的速度匀速运动的所有观察者测量得出的物理学定律必须相互一致。换句话说,就是物理学定律对于所有匀速运动的观察者来说都应该是一样的,不管这些观察者移动得慢还是快,朝着哪个方向。此处的“定律”,指的就是物理量之间的关系。
由于人心难以撼动,斯莫林和罗韦利在政治运动上的抱负遭遇了挫折,但他们在第一次接触到相对性原理的时候,一定对其充满欣慰。至少在物理学的世界里,真正的民主是存在的。
第二条原理则与光速有关。在牛顿力学中,速度是可以简单相加的。如果在一艘横渡大西洋的轮船的甲板上有一个球在滚动,这个球的运动速度就是轮船的速度加上球相对于轮船的速度。但光不遵守这条规则:迈克耳孙–莫雷实验表明,光永远都以一个固定的速率运动。假设一艘轮船以光速 c 运动,那么放在其甲板上的手电筒发出的光相对地面的速度仍然是 c ,而不是 c + c =2 c 。
爱因斯坦并没有尝试解释 为何 光速恒定不变,只是把这当作一个既定的事实,并以此为基础继续推导了下去。
与我们日常生活中熟悉的事物的速度比起来,光速快得令人难以想象。这意味着正常情况下,发生的事件几乎在同时就能被我们看到。在这里发生了一件事,我们瞬间就能看到,过了一会儿在那里又发生了另外一件事,我们也能顺利区分两件事在时间上的先后:这件事先发生,那件事后发生。爱因斯坦提出了一个简单又直接的问题。虽然光看起来好像能够瞬间传播,但它的速度并不是无穷大的。如果光从某个地方出发后,确实需要一定的时间才能到达我们的位置,这对我们观测时空中发生的事件会有什么影响呢?
爱因斯坦发现,光速固定所产生的直接结果,就是绝对时间不存在了。
假设你观察到了一个惊人的现象。在一场雷暴中你看到两道闪电同时击中大地,一道在你左边,一道在你右边(见图2)。你完全静止,一动不动,因此两道闪电发出的光到达你所在处需要的时间是一样的。光传播的速度非常快,因此你在闪电出现之后的短短一瞬间就能同时看到它们。
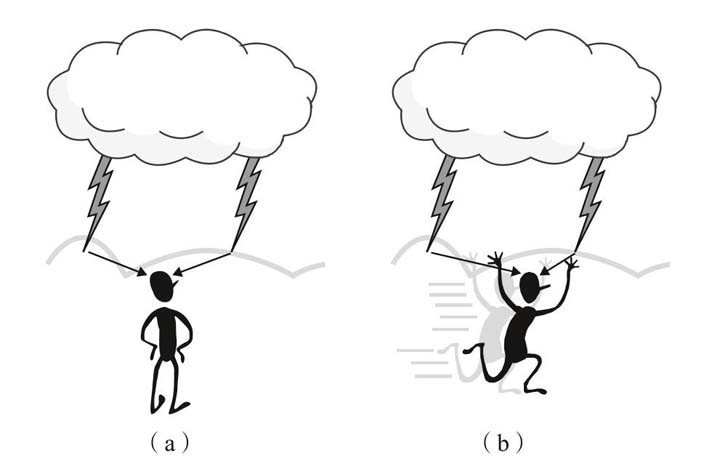
图2

然而,我看到的景象则完全不同。我以很快的速度(比如光速的一半)从左向右移动,在你观察的同时与你擦肩而过。因为我移动的速度非常快,当左边的闪电刚刚赶上我的时候,我已经到达中点右边的某个地方了,因此左边的闪电要多走一段路才能到达我的眼睛。而右边的闪电则少走一段路,因为我已经在向它所在的方向移动了。结果就是右边的闪电先到达我的眼睛,也就是说我先看见右边的闪电出现。
在你眼中,两道闪电同时出现;而在我眼中,则是右边的闪电先于左边的闪电出现。那我们俩当中谁是对的呢?
两个人都对。相对性原理要求物理学定律对于每个人来说都是一样的,与观察者的相对运动无关。就像坐在捷影上的皮平无法区分是自己在移动还是周围的景色在移动一样,我们无法用物理测量手段分辨到底是我在运动还是你在运动。
我们别无选择,只能得出结论:绝对的同时性并不存在。并不存在哪个特定的,或者说“有特权的”惯性参考系,使我们可以宣布在这个参考系里两件事完全同时发生。两件事可能在某一个参考系中同时发生,而在另一个参考系中有先有后,但所有这些参考系都是彼此平等的,它们得到的结果都是准确有效的。因此,“真正的”或绝对的时间不存在。我们所感知的事件各不相同,因为时间是相对的。
你可能已经对这种相对性给出的结果比较熟悉了,这种相对性属于狭义相对论讨论的范畴。狭义相对论之所以名字中带有“狭义”,是因为它并没有涵盖物体在加速的情况(这一点后文还会继续介绍)。在一系列事件发生的时候,相对于事件发生地运动的观察者可能会认为这系列事件发生的时间间隔变长了(与静止的观察者相比),这叫作时间延缓。而相对于静止观察者运动的物体,在静止观察者看来长度会变短(与随物体一起运动的观察者相比)。
时间延缓和长度缩短的程度,取决于观察者的速度与光速的比值。因此,只有在相对速度接近光速的时候,这种效应才足以被观测到。而在日常生活中,无论你车开得有多快,街边站着的人都不会注意到你开的车变短了。
相对论的效应多少有些令人不安,你可能更想退回旧的更熟悉的世界观当中去。如果它只在速度接近光速的时候才出现,那它会不会只是一个观念的问题?从某个惯性参考系观察,时间看起来慢了下来,距离看起来缩短了,但是不是实际上时间并没有变慢,距离也并没有真正缩短?
遗憾的是,它们都是真实存在的。时间和空间是相对的,不是绝对的,而我们也不可能确定一个独特的,或者说“正确的”视角,然后给出关于距离和时间的绝对的度量。相对论效应产生的结果是非常实际的。公平来讲,我们还很难通过实验来证实距离的缩短
 ,但我们可以精确地测量出时间的延缓。如果在飞机上放一台原子钟,让它从英国伦敦飞到美国华盛顿特区再飞回来,我们会发现它比一直放置在英国国家物理实验室里的静止的钟慢了1.6×10
–8
秒。这是因为在飞机两次飞越大西洋的过程中,飞机上的时间延缓了。
,但我们可以精确地测量出时间的延缓。如果在飞机上放一台原子钟,让它从英国伦敦飞到美国华盛顿特区再飞回来,我们会发现它比一直放置在英国国家物理实验室里的静止的钟慢了1.6×10
–8
秒。这是因为在飞机两次飞越大西洋的过程中,飞机上的时间延缓了。

这可能很难理解,而且其结果十分令人震惊。年轻的罗韦利意识到,在狭义相对论中,说多个地方同时处于“现在”这个时刻是没有意义的。在很多方面,“现在”只是个幻觉,就好像过去人们认为地面是平的,但这只是以我们的角度无法察觉地面的弯曲所产生的幻觉罢了。如果我们能通过某种方法以十亿分之一秒的精度感知时间,我们就会意识到,说“此时此地”是有意义的,但说事件“此时发生”整个宇宙就没有意义了。
 尝试建立一套绝对的时间标度,给宇宙中事件发生的时间先后排序,这是注定不可能做到的,就好像在北极点寻找北方一样。
尝试建立一套绝对的时间标度,给宇宙中事件发生的时间先后排序,这是注定不可能做到的,就好像在北极点寻找北方一样。
在对相对论产生的这些结果进行了漫长而艰难的思索之后,爱因斯坦于1905年的晚些时候为他关于相对论的论文发表了一篇短小的附录。他将同样的逻辑应用在一个同时发出两道光的物体上。物体发出的两道光方向相反、能量相等,因此不会改变物体的直线运动方向。他推导出,在相对这个物体运动的惯性参考系看来,物体发出的光所带走的总能量要更大一些,就同时间延缓一样。
然而,有一条物理定律规定能量必须永远守恒。能量不可能被创造,也不可能被消灭。因此,如果这个参考系测量到光带走的能量更多,那这些额外的能量是从哪里来的呢?我们可能直觉上会假设这个物体的速度必须减慢,由此失去一部分动能,从而转移给发出的光。但爱因斯坦发现,事情并非如此。他发现,这些能量确实来自物体的动能,但不是物体的速度变慢了,而是物体的质量变小了。物体的质量与能量满足这样一个关系式: m = E / c 2 。
爱因斯坦得出结论:
如果一个物体以辐射的形式发射出能量
E
,它的质量就会减少
E
/
c
2
。如果我们只说辐射出的能量来自物体本身,听起来就显得太可有可无了,因此我们总结了一个更普遍的结论:物体的质量是它所含能量的量度。

如今的我们可能会直接把这段话的含义表述为这一经典的公式: E = mc 2 。
在1905年爱因斯坦发表狭义相对论的附录之后,这一理论的简洁性达到了惊人的程度。它并不需要多么复杂的数学计算,但它的意义是极为深远的。学生时期的斯莫林和罗韦利为相对论的逻辑所震惊,也为它得出的结论而着迷。
但如果牛顿在爱因斯坦身后看到这些工作,他或许还是会忍不住露出一丝微笑。
之前提到过,爱因斯坦的狭义相对论之所以称为“狭义”,是因为它只适用于匀速运动的系统,并不适用于带有加速度的系统。尽管我们承认匀速直线运动是相对的,但任何一个坐过过山车的人都会告诉你,加速度是一种可以被实际感受到的东西。皮平在捷影背上时意识不到自己在匀速运动,但如果我们的速度突然发生改变,或者绕着什么东西转圈,我们就会感觉到。
但加速度是相对于什么而加速的呢?旋转又是相对于什么而旋转的呢?尽管狭义相对论取得了巨大的成功,但爱因斯坦尚未能完全抛弃绝对空间和时间。
不仅如此,牛顿还根据自己得出的运动定律推导出了一条普适的引力定律。牛顿引力定律表明,所有物体之间都有一种吸引力,其大小跟物体的质量成正比,并与物体之间的距离的平方成反比。因此,在引力的表达式中,我们只需要把质量相乘,并除以距离的平方。
牛顿引力定律取得了巨大的成功,但它也有自己的代价。牛顿的引力与他的运动定律里涉及的力有显著的区别:后者是接触性的,它们通常通过对物体的物理接触来起到作用效果,即改变物体的运动状态,比如让物体从静止开始运动。
但牛顿的引力的作用机制则完全不同。引力似乎可以瞬间在两个相隔一定距离的物体之间发生作用,好像是一种神秘的“超距作用”。关于这种作用是如何实现的,物理学家一无所知。牛顿还因为引入了“神秘力量”而遭到了批评。
对此,牛顿自己也毫无办法。在他1713年出版的名扬天下的著作《自然哲学的数学原理》第二版中,他以评注的方式加入了一段一般性的讨论,写道:“我一直未能从引力现象中发现引力性质的成因,也没有形成任何猜想。”

因为牛顿的万有引力被认为是瞬间施加于物体身上的,不管它们之间相隔有多远都是如此,所以这种经典引力观完全违背狭义相对论——狭义相对论认为没有哪种力的传播速度能超过光速。
狭义相对论不适用有加速度的情况,也无法与牛顿引力定律相调和。爱因斯坦还有很多工作要做。