




地图是GIS中的一个基础概念,是按照一定数学法则,用符号、图形或数字的形式表示地理空间信息的一种载体。地图最基本的概念是它的空间坐标属性,即地理参考(georeference),也就是在地球表面的具体位置。为了精确地记录地球表面任一地点的准确位置,在测量学中发展了地理坐标系统。要定义一个地理坐标系统就必须首先定义地球表面的形状。我们知道地球为一个不规则的椭球体,因此需要用一个与地球形状最接近的规则椭球体来代替不规则的地球球面,作为大地测量的基础,这个规则的椭球体称为“地球椭球体”(Earth ellipsoid)(文本框1-1)。
文本框1-1 地球椭球体
地球椭球体的大小和形状主要由三个参数决定:长 半轴(a),短半轴(b)和扁率(f)。其中,长半径(a)即赤道半径,短半径(b)即极半径。扁率f=(a-b)/a, 表示椭球体的扁平程度。
目前,国内常用的地球椭球体有“克拉索夫斯基椭球体”“IAG 75椭球体”和“WGS 84椭球体”,它们的参数如下:
椭球体 长半轴 短半轴
Krassovsky 6378245 6356863.0188
IAG75 6378140 6356755.2882
WGS84 6378137 6356752.3142
以地球椭球体为基础可以建立起不同的球心坐标系(polar coordinate)或地理坐标系(geographical coordinate)。GIS一般使用地理坐标系。地理坐标系以经纬度的形式表示地球表面上任一点的空间坐标,其中经度为经过该点的子午线与位于伦敦格林尼治天文台的零子午线之间的夹角,纬度为经过该点的纬度线与地球赤道线之间的夹角。在测量学中,大地经纬度是根据一个称为“大地原点”的起始点的大地坐标,按照大地测量结果的数据推算,因此选择不同的“大地原点”和地球椭球体可以建立不同的大地地理坐标系。我国目前常用的大地地理坐标系有“1954年北京坐标系”“1980国家大地坐标系”和“2000国家大地坐标系”(文本框1-2)。
文本框1-2 我国目前常用的大地坐标系
1954年北京坐标系:我国20世纪50年代参照苏联的克拉索夫斯基椭球体建立的大地坐标系,大地原点在苏联境内。尽管后来利用这个坐标系做了大量的测绘工作,但由于一些诸如大地原点不在我国境内、椭球面与我国境内大地水准面不吻合等情况,利用这个坐标系测绘的精度不高。
1980年国家大地坐标系:也称为1980年西安坐标系。我国20世纪70年代建立的国家大地坐标系,大地原点选在陕西省永乐镇,采用了国际大地测量协会推荐的1975地球椭球体(IAG75)。该坐标系的椭球面与我国境内的大地水准面密合最佳。
2000年国家大地坐标系:由国家测绘局公布自2008年7月1日起使用的国家大地坐标系。该坐标系是全球球心坐标系,其原点为包括海洋和大气的整个地球的质量中心,椭球体采用国际通用的WGS 84椭球体。
尽管采用大地地理坐标可以准确地描述地球表面任意点的空间位置,但采用经纬度的记录方式在实际应用中却并不方便。首先,经纬度的方式只适用于球面,却不能表示在二维的平面直角坐标系中,而地图和计算机屏幕的显示都是二维坐标;其次,直接使用经纬度不方便在实际应用中的数据测量和计算,比如已知两个遗址点的经纬度坐标,并不能直接计算出它们之间的距离。因此,一般情况下还需要将大地坐标转换成平面直角坐标,而这个转换过程即地图投影。
理论上不经过地图投影无法将地球表面的曲面转换成平面,而经过地图投影就一定会产生投影变形。投影变形对地图的影响主要取决于两个因素:其一,地图范围的大小,也就是地图的比例尺。一般来说,地图的范围越大,比例尺越小,投影产生的变形就越显著;相反,地图的范围越小,或者比例尺越大,投影产生的变形就越不明显。比如,在足够小的测量范围内,我们可以近似地以平面直角坐标直接代替地球球面坐标。其二,投影方式的不同。对地球上的不同区域而言,不同的投影方式产生的变形会完全不同,因此我们应该根据研究区域和研究需要确定具体的投影方式。比如,等角横切圆柱投影在靠近赤道地区的投影变形影响较小,而在两极地区的变形则十分明显。
目前已经发展出多种投影方式可以应用在全球或区域范围内的各种比例尺地图上,而一般的GIS软件也都集成有这些常用的投影方式,比如GRASS软件就集成了123种地图投影的方式。这些地图投影可以根据不同的属性进行分类:
1. 如果按照投影面与地球表面的关系可以分为“切投影”和“割投影”,前者投影面与地球表面相切,后者则相割。而无论是相切还是相割,切线和割线处的投影变形最小。
2. 如果按照投影面的形状则可分为“圆锥投影”“圆柱投影”和“方位投影”,它们分别使用圆锥体、圆柱体和平面作为投影面,而按照圆锥、圆柱的轴线以及平面投影的垂线与连接地球南北两极的轴线之间的角度关系,又有“正轴”“横轴”和“斜轴”的差别(图1-3)。
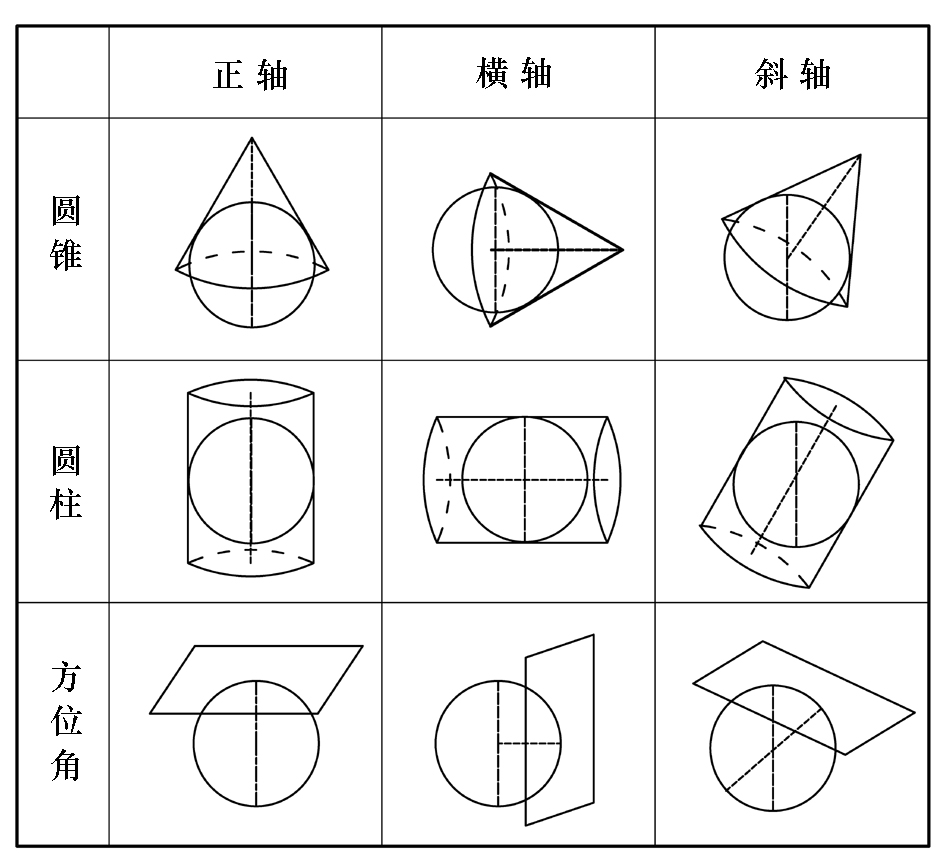
图1-3 地图投影的方式
3. 如果按照投影变形的方式,则可分为“等角投影”“等积投影”和“等距投影”。等角投影保持了经度线和纬度线之间的90度关系,从而使得地球表面任意两点间的角度在投影后保持不变,但代价是投影面积的变形;等积投影则正好相反,保持了投影后的面积不变,但投影角度的变形较大;等距投影保持了在标准经纬度线上无长度变形,但却只能应用在一个方向上。
实践中,正轴圆锥投影能够保持经度线为汇聚向极轴的直线,而纬度线为平行弧线。离切线或割线越近的纬度线处的投影变形越小,反之则越大。如果将投影变形均匀分配在南北两极之间的纬度线上则称为“等距圆锥投影”;而如果将投影变形压缩在南北两极,同时保持投影面积不变则为“等积圆锥投影”,如中小学地理教科书中常见的“Albers投影”(图1-4)即为等积割圆锥投影。
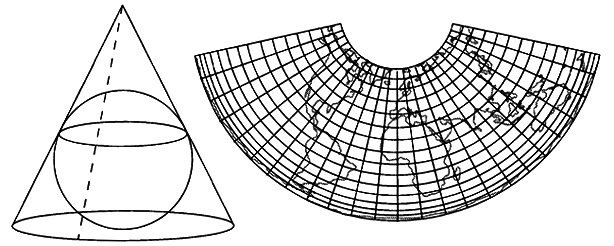
图1-4 Albers投影(引自:Conolly & Lake 2006,20页)
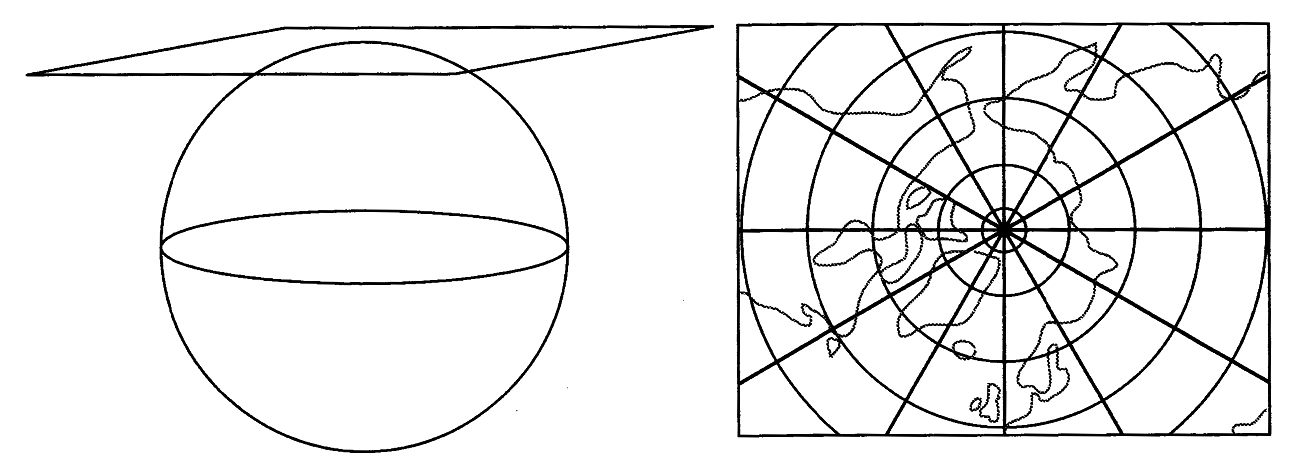
图1-5 方位角投影(引自:Conolly & Lake 2006,20页)
方位角投影(图1-5)采用与地球表面相切于一点的平面为投影面,理论上任意一点都可以作为切点,但实际上只是在表现地球南北两极地区的地图时才使用这种投影,并以南北极为切点。这种投影为等角投影,保持了纬度线圈与从中心点散发的经度线之间的角度关系,因此从中心点出发的角度和距离是相等的,但距离中心点越远,面积变形越大。
圆柱投影采用等角投影的方式,保持经纬度线之间的夹角为90度,在切线附近的投影变形最小,而距离切线越远,投影变形越大。圆柱投影的方式尤其适合于区域性的大比例尺地图,其中最常用的是高斯投影和横轴墨卡托投影(图1-6)。
高斯投影又称为高斯—克吕格投影,是一种等角横轴切圆柱投影。高斯投影首先假想用一个圆柱横切于地球椭球体的某一经线上,这条与圆柱面相切的经线,称中央经度线。以中央经度线作为投影的对称轴,将东西每3°或1°30′的两条经度线所夹经差6°或3°的带状地区按数学方法投影到圆柱面上,再展开成平面,即形成高斯投影带(图1-7)。
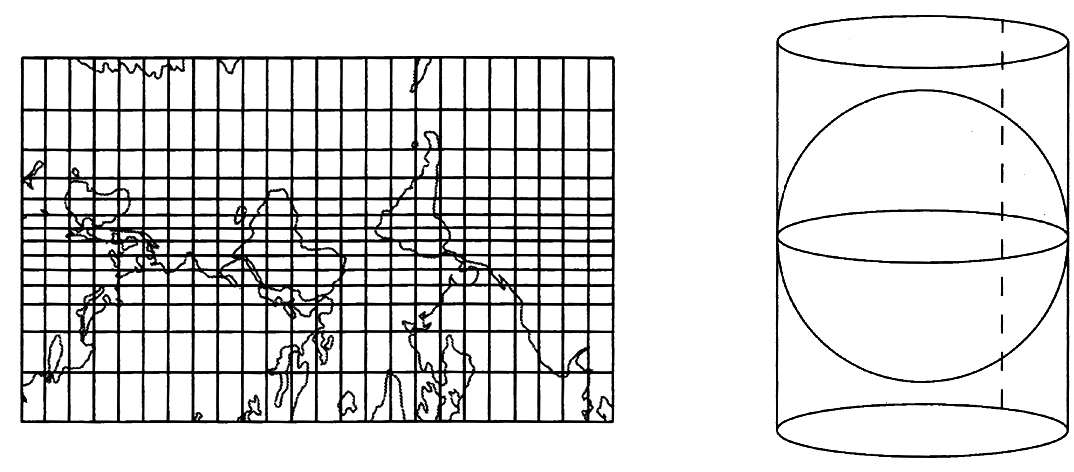
图1-6 等角圆柱投影(引自:Conolly & Lake 2006,21页)
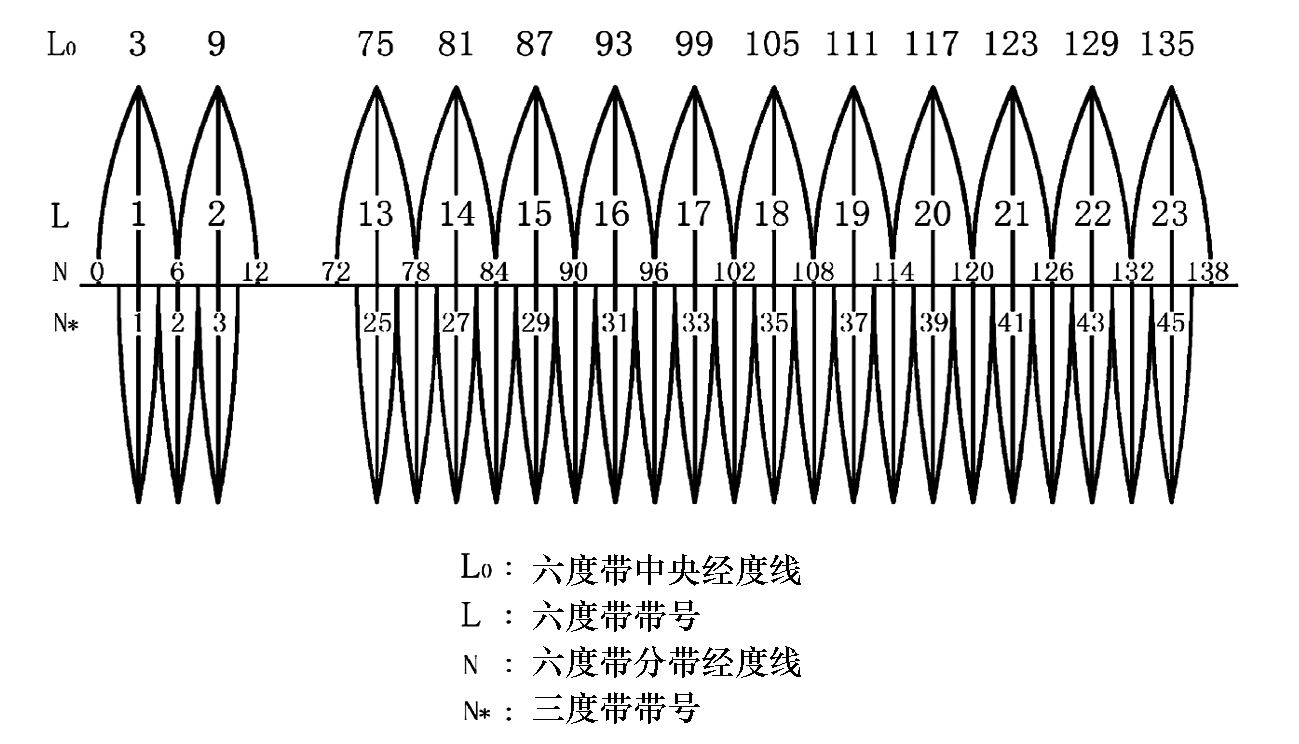
图1-7 高斯投影带
在每个高斯投影带的平面上,中央经度线与赤道形成相互垂直的两条直线,分别作为高斯平面直角坐标系的纵轴( x轴)和横轴(y轴),两轴的交点O作为坐标的原点,同时规定x轴向北为正,y轴向东为正。对于我国的情况而言,领土范围均位于北半球,境内纵坐标x值均为正数,横坐标y值则 有正有负。因此,在实际应用中,为了计算方便,通常将每个投影带的坐标原点向西平移500公里,使整个投影带中任意一点的横坐标 y 都为正值(图1-8)。
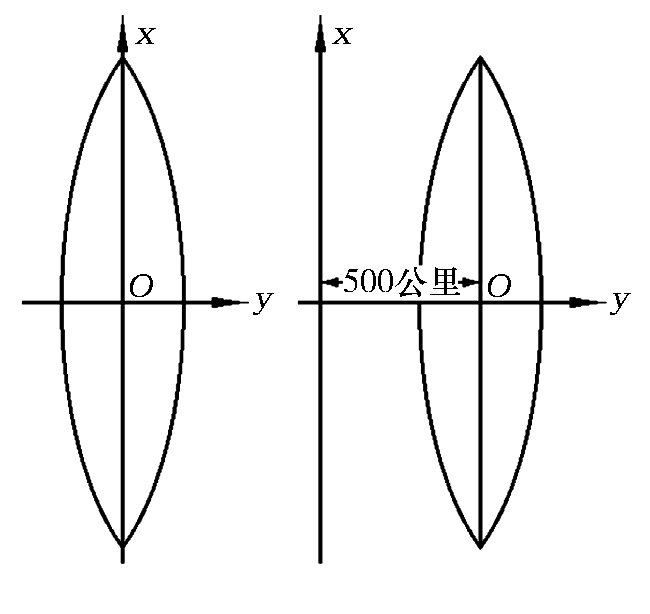
图1-8 高斯投影带的坐标系(引自:刘建国 2008,13页)
横轴墨卡托投影即国际上通用的UTM投影,是一种等角横轴割圆柱投影。横轴墨卡托投影假设圆柱割地球于南纬80度、北纬84度两条等高圈,投影后经度线是一组垂直的等距离平行直线,纬线是垂直于经线的一组平行直线。各相邻纬线间隔由赤道向两极增大。一点上任何方向的长度比均相等,即没有角度变形,而面积变形显著,随与标准纬线的距离增大而增大。UTM投影保持了方向和角度的正确,因此最初被广泛应用于航海。目前,UTM投影是国际上使用最为广泛的投影方式之一。
UTM投影分带方法与高斯投影相似,将北纬84度至南纬80度之间按经度分为60个带,每带6度,但中央经度线的投影比例系数为0.9996。
一般情况下在GIS软件中首先要定义图层的地理坐标系,多数常用的地理坐标系都被集成在GIS的软件包中,可以直接调用。但我们也可以使用自定义的坐标系统。自定义坐标系时首先要选择合适的地球椭球体和正确的投影方式,并设置相关的投影参数,比如中央经度线的度数、南北方向位移量以及投影比例等。由于不同区域的投影变形量不同,因此在使用大比例尺地图时,还应该设置相应地区的投影转换参数,其中常用的有“三参数”和“七参数”,它们都可以通过实地测量计算得到。