




面积问题包含两个方面:一是给出面积的定义,二是寻求计算面积的方法。
设f是定义在[a,b]上的非负函数,称由曲线y=f(x)与直线x=a,x=b,y=0所围成的平面图形为曲边梯形。如何定义这个曲边梯形的面积,其面积又如何来计算呢?
作区间[a,b]的一个分划
D:a=x 0 <x 1 <…<x n =b.
那么分划D把[a,b]分为n个小区间,每个小区间[x i-1 ,x i ]的长度为∆x i =x i -x i-1 .在[x i-1 ,x i ]上任取一点ξ i ,那么以直线y=f(ξ i ),x=x i-1 ,x=x i ,y=0围成的小矩形的面积为f(ξ i )∆x i ,将它作为小区间[x i-1 ,x i ]上对应的小曲边梯形的面积的近似。把这n个小矩形面积相加便得到
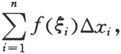
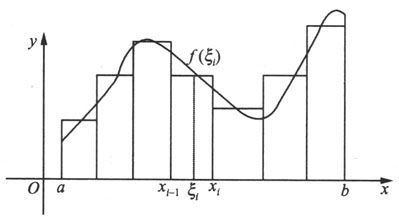
图 5.1.1
它就是所考虑的大曲边梯形的面积的近似。记
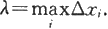 如果分划越来越细,即λ→0时,上述和式的极限存在,就定义这个大曲边梯形的面积A为这个极限,即
如果分划越来越细,即λ→0时,上述和式的极限存在,就定义这个大曲边梯形的面积A为这个极限,即
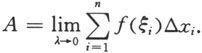
设一质点作直线运动,已知它在时刻t的速度为v(t),要求它在时段[a,b]中的位移s.
当速度v(t)是常数v 0 ,即质点作匀速直线运动时,则s=v 0 (b-a).但是,当质点作变速直线运动时,s(t)的计算就不这么简单了。为了计算质点在时段[a,b]中的位移,我们作时段[a,b]的一个分划
D:a=t 0 <t 1 <…<t n =b,
那么D把[a,b]分为n个小区间,每个小区间[t i-1 ,t i ]的长度为∆t i =t i -t i-1 .在[t i-1 ,t i ]上任取一点ξ i ,用质点在时刻ξ i 的速度去近似时段[t i-1 ,t i ]的速度,即将质点在时段[t i-1 ,t i ]中的运动近似看成匀速直线运动,则质点在时段[t i-1 ,t i ]的位移就近似地为v(ξ i )∆t i .于是

就是质点在时段[a,b]中的位移的近似。
记
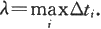 当每个小时段越短,即λ越小,这种以匀速代变速的精确度越高,从而质点在时段[a,b]中的位移为
当每个小时段越短,即λ越小,这种以匀速代变速的精确度越高,从而质点在时段[a,b]中的位移为
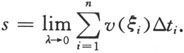
以上的几何量和物理量的计算方法,都是先做分割、再求和,最后取和式的极限。这种形式的极限,还出现于大量其他问题的计算之中。撇开各类问题的具体背景,抽象出其数量关系的共同特征,就引出了下述定积分的概念。
定义5.1.1 设函数f是[a,b]上的有界函数,作[a,b]的任意分划
D:a=x 0 <x 1 <…<x n =b,
并记∆x i =x i -x i-1 为小区间[x i-1 ,x i ]的长度(i=1,2,…,n).任取ξ i ∈[x i-1 ,x i ],作和式
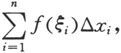
称之为黎曼(Riemann)和。记
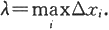 如果当λ→0时黎曼和的极限存在,且极限值与分划D以及ξ
i
(i=1,2,…,n)的取法无关,则称此极限值为f在[a,b]上的(黎曼)积分,简称为定积分,记做
如果当λ→0时黎曼和的极限存在,且极限值与分划D以及ξ
i
(i=1,2,…,n)的取法无关,则称此极限值为f在[a,b]上的(黎曼)积分,简称为定积分,记做
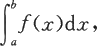 即
即
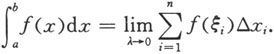
这时称f是[a,b]上的(黎曼)可积函数,简称为可积函数,也称f在[a,b]上可积。
在记号
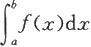 中,称f为被积函数,x为积分变量,并分别称a,b为积分的下限与上限,
中,称f为被积函数,x为积分变量,并分别称a,b为积分的下限与上限,
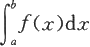 也称为积分值。
也称为积分值。
对定积分的定义,要作两点补充说明。
1.定积分是个数值,它仅与被积函数、积分的上、下限有关,而与积分变量符号的选取无关,因此
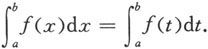
2.在定积分的定义中要求a<b.为了运算和应用的方便,当a>b时补充规定
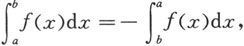
并且当b=a时,规定
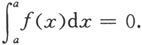
注意,并不是所有函数都是可积的。
例5.1.1 讨论狄利克雷(Dirichlet)函数
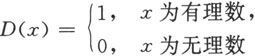
在[0,1]上的可积性。
解 由于有理数和无理数在实数集上的稠密性,因此不管用什么样的分划
D:0=x 0 <x 1 <…<x n =1.
对[0,1]作分割,在每个小区间[x i-1 ,x i ]中一定既有有理数,又有无理数(i=1,2,…,n).
于是,当将ξ i ∈[x i-1 ,x i ]全部取为有理数时,成立
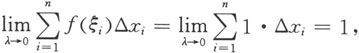
而当将ξ i ∈[x i-1 ,x i ]全部取为无理数时,则有
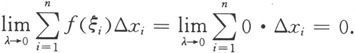
尽管以上两个黎曼和的极限都存在,但极限并不相同,所以狄利克雷函数在[0,1]上是不可积的。
那么什么样的函数是可积的呢?我们对此不进行深入讨论,只给出两个充分条件。
定理5.1.1 设函数f在闭区间[a,b]上连续,则f在[a,b]上可积。
事实上,以上定理还可推广为:设函数f在[a,b]上有界,且f在[a,b]上仅有有限个不连续点,则f在[a,b]上可积。
定理5.1.2 设函数f在闭区间[a,b]上单调,则f在[a,b]上可积。
例5.1.2 计算定积分
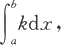 其中k是一个常数。
其中k是一个常数。
解 因为对[a,b]的任何分划D:a=x 0 <x 1 <…<x n =b和任何ξ i ∈[x i-1 ,x i ](i=1,2,…,n),均有
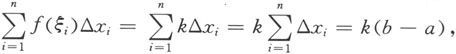
所以
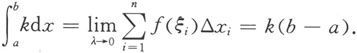
注 今后常把定积分
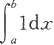 记为
记为
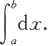
例5.1.3 计算定积分
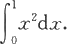
解 因为f(x)=x
2
在[0,1]上连续,由定理5.1.1知它在[0,1]上可积。既然积分值与区间的分划及ξ
i
的取法无关,不妨把[0,1]分为n等份,即取x
i
=
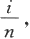 因此
因此
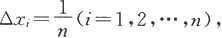 再取ξ
i
=x
i
.这时黎曼和为
再取ξ
i
=x
i
.这时黎曼和为
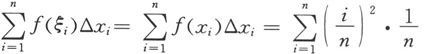
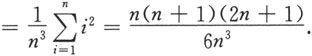
由于
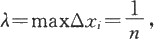 所以当λ→0时,n→∞.于是
所以当λ→0时,n→∞.于是
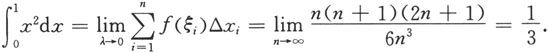
由于定积分是黎曼和的极限,虽然形式上这种极限与函数极限稍有不同,但本质上并没有什么差别,因此定积分的一些性质,可以利用极限的相应性质推导出来。
定理5.1.3 设函数f和g在[a,b]上可积,α,β为常数,则函数αf+βg也在[a,b]上可积,且成立
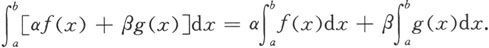
证 因为对[a,b]的任何分划D:a=x 0 <x 1 <x 2 <…<x n =b和任何ξ i ∈[x i-1 ,x i ](i=1,2,…,n)均成立
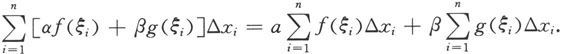
令
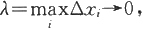 由于函数f和g都在[a,b]上可积,所以
由于函数f和g都在[a,b]上可积,所以
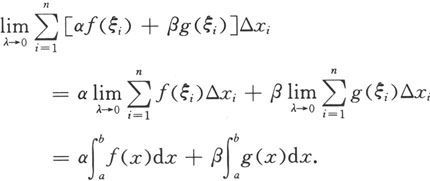
由定义知函数αf+βg在[a,b]上可积,且
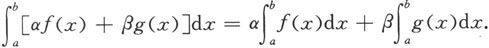
证毕
定理5.1.4 设函数f和g都在[a,b]上可积,则函数f·g在[a,b]上也可积。
这个定理的证明从略。要注意的是,一般来说
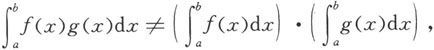
请读者自行举例说明。
定理5.1.5 设函数f在[a,b]上可积,则对任意c∈[a,b],f在[a,c]和[c,b]上都可积;反之,若函数f在[a,c]和[c,b]上都可积,则f在[a,b]上也可积。此时成立
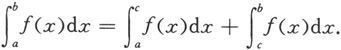
这个定理的证明从略。
注意上述公式在c在[a,b]之外时也成立。例如,当a<b<c时,若函数f在[a,b]和[b,c]上可积,则由以上定理得
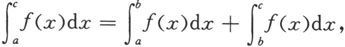
移项便得
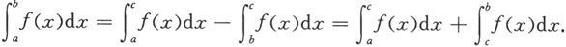
定理5.1.6 设函数f和g都在[a,b]上可积,且在[a,b]上成立f(x)≤g(x),则
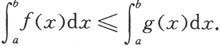
这个定理的证明可由极限的保序性质直接得到。
定理5.1.7 设函数f在[a,b]上可积,则函数∣f∣在[a,b]上也可积,且成立
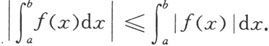
函数∣f∣在[a,b]上的可积性证明从略。不等式是源于
-∣f(x)∣≤f(x)≤∣f(x)∣
和定理5.1.6的结论。
定理5.1.8 设f是[a,b]上的连续函数,则在[a,b]上至少存在一点ξ,使得
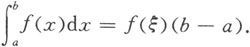
证 因为函数f在[a,b]上连续,则它在[a,b]上必能取到最大值M和最小值m.从
m≤f(x)≤M,x∈[a,b],
以及定理5.1.6和例5.1.2得
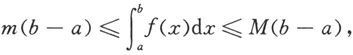
因此
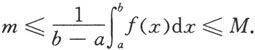
再由连续函数的介值定理知,必存在ξ∈[a,b],使得
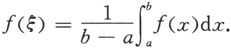
证毕
积分中值定理有明确的几何意义:若f是[a,b]上的非负函数,则必存在ξ∈[a,b],使得以[a,b]为底,f(ξ)为高的矩形面积恰好等于由曲线y=f(x)与直线x=a,x=b,y=0所围成的曲边梯形的面积(见图5.1.2).
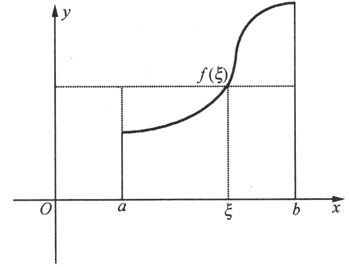
图 5.1.2
数值
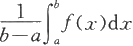 称为函数f在[a,b]上的积分均值。
称为函数f在[a,b]上的积分均值。
读者可能已经发现,利用定义来直接计算定积分是非常困难的。微积分基本定理说明,定积分的计算可以转化为求被积函数的原函数或不定积分问题,从而使定积分的计算有了强大而有效的一般方法。
设函数f在[a,b]上可积,则对于任意给定的x∈[a,b],f在[a,x]上可积,于是定积分
 就有唯一确定的值。这样就确定了一个[a,b]上的函数
就有唯一确定的值。这样就确定了一个[a,b]上的函数

称之为变上限积分。
类似地,

也是一个[a,b]上的函数,称之为变下限积分。变上限积分与变下限积分统称为变限积分。
定理5.2.1 设函数f在[a,b]上可积,则函数

在[a,b]上连续。
证 我们只证函数F在(a,b)上连续,F在x=a点的右连续性与在x=b点的左连续性类似可证。
因为函数f在[a,b]上可积,所以函数f在[a,b]上有界,因此存在常数M>0,使得
∣f(x)∣≤M,x∈[a,b].
设x∈(a,b),则当x+∆x∈(a,b)时成立

所以

因此
 即函数F在x点连续。
即函数F在x点连续。
证毕
进一步,若函数f还在[a,b]上连续,则函数F还在[a,b]上可导,这就是:
定理5.2.2 设函数f在[a,b]上连续,则函数

在[a,b]上可导,且导数(导函数)为
F′(x)=f(x),x∈[a,b].
证 我们只证在(a,b)上定理的结论成立,在区间[a,b]的端点的结论类似可证。
设x∈(a,b),则当x+∆x∈(a,b)时成立

由中值定理知,在x和x+∆x之间存在ξ,使得

于是
F(x+∆x)-F(x)=f(ξ)∆x.
因为当∆x→0时,x+∆x→x,从而ξ也趋向x,利用f的连续性便得

这说明函数F在x点可导,且成立
F′(x)=f(x).
证毕
从定理5.2.2立即得到
定理5.2.3(原函数存在定理) 设函数f在[a,b]上连续,则函数

是f在[a,b]上的原函数。
推论5.2.1 设函数f在[a,b]上连续,函数g,h在[a,b]上可导,且满足
a≤g(x)≤b,a≤h(x)≤b,x∈[a,b].
则函数

在[a,b]上可导,且满足
P′(x)=f[h(x)]h′(x)-f[g(x)]g′(x),x∈[a,b].
证 记
 则在[a,b]上成立F′(u)=f(u).
则在[a,b]上成立F′(u)=f(u).
因为

所以由复合函数的求导法则得
P′(x)=F′[h(x)]h′(x)-F′[g(x)]g′(x)
=f[h(x)]h′(x)-f[g(x)]g′(x).
证毕
例5.2.1 设
 求F′(x).
求F′(x).
解 由推论5.2.1得

例5.2.2 求极限

解 由定理5.2.1知,这是
 型的极限,所以由推论5.2.1及洛必达法则得
型的极限,所以由推论5.2.1及洛必达法则得

定理5.2.4(牛顿-莱布尼茨公式) 设函数f在[a,b]上连续,函数F是f在[a,b]上的一个原函数,则

这个定理也称为微积分基本定理。
证 记

由定理5.2.3知,函数G是f在[a,b]上的一个原函数。又已知F也是f在[a,b]上的一个原函数,于是这两个函数只能相差一个常数,即存在常数c,使得
G(x)=F(x)+c,x∈[a,b],
即

取x=a便得0=F(a)+c,即c=-F(a).再取x=b,便得

证毕
注 在牛顿-莱布尼茨公式中,常简记F(b)-F(a)为
 于是
于是

例5.2.3 求定积分

解 显然
 是
是
 的一个原函数,所以由牛顿-莱布尼茨公式得
的一个原函数,所以由牛顿-莱布尼茨公式得

例5.2.4 求定积分

解 由定积分的线性性质和牛顿-莱布尼茨公式得

例5.2.5 求定积分

解 因为

由定积分的区间可加性和牛顿-莱布尼茨公式得

由牛顿-莱布尼茨公式可知,要计算定积分,只要求出被积函数的一个原函数,再将定积分的上、下限代入该原函数即可。如果被积函数比较复杂,自然可以利用不定积分的换元法和分部积分法求出它的原函数,再将定积分的上、下限代入便可计算出定积分的值。然而,在许多理论和实际问题中,还需要直接利用定积分的换元积分法和分部积分法。
定理5.3.1 设函数f(x)在区间[a,b]上连续,函数x=φ(t)在区间[α,β](或区间[β,α])上有连续导数,满足φ(α)=a和φ(β)=b,且函数φ的值域包含于[a,b].则成立

证 因为函数f在区间[a,b]上连续,所以必有原函数。设F为f在区间[a,b]上的一个原函数,由复合函数求导法则可知
[F(φ(t))]′=F′(φ(t))φ′(t)=f(φ(t))φ′(t),
因此F(φ(t))是f(φ(t))φ′(t)一个原函数。由牛顿-莱布尼茨公式便得

证毕
注意,换元后的定积分
 的上下限α和β必须与原定积分的上下限a和b相对应,而不必考虑α与β之间的大小。
的上下限α和β必须与原定积分的上下限a和b相对应,而不必考虑α与β之间的大小。
例5.3.1 算定积分

解法一 令
 则
则
 因为φ(1)=1,φ(8)=2,积分区间x∈[1,2]对应于t∈[1,8].应用换元积分公式便得到
因为φ(1)=1,φ(8)=2,积分区间x∈[1,2]对应于t∈[1,8].应用换元积分公式便得到

解法二 易知

令u=ψ(x)=x 3 ,则ψ(1)=1,ψ(2)=8,于是由换元积分公式得

从上例可以看出,换元积分公式

可以从左端推到右端,也可以从右端推到左端。解法一就是采用从左端推到右端的方法,这相当于不定积分的第二类换元积分法;解法二则是采用从右端推到左端的方法,这相当于不定积分的第一类换元积分法,即“凑微分法”.读者应该对具体的问题作具体的分析,选择恰当的变量代换,从而简化计算过程。
例5.3.2 求半径为a的圆的面积。
解 设圆的方程为
x 2 +y 2 =a 2 ,

图5.3.1
利用对称性,我们只需求它在第一象限部分的面积,其4倍就是整个圆的面积。
在第一象限,圆的方程可变为

因此,相应的四分之一圆面积为

为计算这个积分,作变量代换x=asint,于是dx=acostdt,积分区间x∈[0,a]对应于
 于是
于是

所以,整个圆的面积为S=πa 2 .
例5.3.3 计算定积分

解 作变量代换
 则x=ln(1+u
2
),所以
则x=ln(1+u
2
),所以
 由于当x=0时,u=0;当x=ln2时,u=1,于是
由于当x=0时,u=0;当x=ln2时,u=1,于是

要补充说明的是,如果在计算中使用的是“凑微分”的换元法,在计算过程往往不必另行写出中间变量,因而也毋须引入中间变量的变化区间。这就是说,如果F(u)是f(u)的原函数,φ(x)在[a,b]上具有连续导数,且φ的值域包含于f的定义域,则

例5.3.4 计算

解 利用“凑微分”法得

定理5.3.2 设函数f在对称区间[-a,a]上连续,则

从而
(1)若f是偶函数,则

(2)若f是奇函数,则

证 由于

对积分
 作变量代换x=-t得
作变量代换x=-t得

于是

证毕
这个定理中的结论(1)和(2)的几何意义是非常明显的,并且它们可使定积分的计算更为简单。例如,从结论(2)立刻可知

这是因为被积函数是奇函数。
例5.3.5 计算

解 因为cosxsin 2 x是偶函数,cosxsin2x是奇函数,由定理5.3.2得

例5.3.6 计算定积分

解 由定积分的区间可加性得

对等式右边的第二个积分作变量代换x=π-t得

于是

注意,在本题中我们实际上并没有求出函数
 的原函数,只是利用换元积分法把不易计算的部分消去了。因此定积分换元法的使用是有其自身特点的,不要简单地认为它与不定积分的换元法的作用相同。
的原函数,只是利用换元积分法把不易计算的部分消去了。因此定积分换元法的使用是有其自身特点的,不要简单地认为它与不定积分的换元法的作用相同。
设函数u和v在区间[a,b]上有连续导数。由函数乘积的求导公式
(uv)′=uv′+vu′
可得
uv′=(uv)′-vu′.
将上式在[a,b]上取定积分便得

这样便有如下的分部积分公式:
定理5.3.3 设函数u和v在[a,b]上有连续导数,则

上式也可表成下列形式

例5.3.7 计算定积分

解 应用分部积分公式得

例5.3.8 计算定积分

解 作变量代换
 则x=t
2
-1,dx=2tdt,所以
则x=t
2
-1,dx=2tdt,所以

应用分部积分公式得

因此

例5.3.9 计算定积分
 (n为正整数).
(n为正整数).
解 显然

当n≥2时,利用分部积分法得

于是得到递推关系

从这个递推关系得

例5.3.10 计算定积分

解 作变量代换x=sint得

由例5.3.9知

所以
