下载掌阅APP，畅读海量书库
立即打开
空间解析几何是在三维坐标系中，用代数方法研究空间曲面和曲线的几何性质的一种数学理论。
我们知道，建立了平面直角坐标系后，平面上的每一点都与其坐标一一对应，这样就定量地确定了平面上的每一点位置。为了定量地确定空间上每一点的位置，同样需要建立空间直角坐标系。
在空间取定一点O，过点O作三条相互垂直的数轴，它们都以O为原点，且都取相同的长度单位。这三条数轴通常分别称为x轴，y轴和z轴，统称为坐标轴。它们的正向要符合右手定则，即以右手握住z轴，当右手的四个手指从x轴正向转过π/2角度后指向y轴正向时，拇指的指向就是z轴的正向（见图6.1.1）．这样，三条坐标轴就构成了一个空间直角坐标系，常称为Oxyz坐标系。点O称为坐标原点，简称原点。习惯上把x轴和y轴配置在水平面上，而z轴则垂直向上，当然它们要符合右手定则。
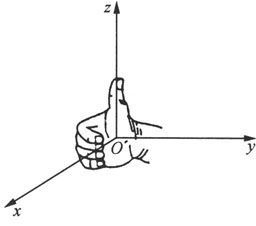
图 6.1.1
由x轴和y轴确定的平面称为Oxy平面，由y轴和z轴确定的平面称为Oyz平面，由z轴和x轴确定的平面称为Ozx平面。它们统称为坐标平面。三张坐标平面把空间分成八个部分，每一部分叫做卦限。含有x轴，y轴和z轴正半轴的那个卦限称为第Ⅰ卦限，第Ⅱ、第Ⅲ、第Ⅳ卦限在Oxy平面上方，依逆时针方向依次确定。第Ⅴ、Ⅵ、Ⅶ、Ⅷ卦限在Oxy平面下方，由第Ⅰ卦限之下的第Ⅴ卦限，依逆时针方向依次确定。
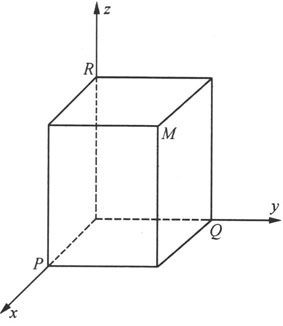
图 6.1.2
对于空间上的任一点M，过点M作三张平面分别垂直于x轴，y轴和z轴，且与这三个轴分别交于P，Q，R三点（见图6.1.2），这三点在x轴，y轴和z轴的坐标为依次为x，y，z，那么点M唯一确定了一个三元有序数组（x，y，z）；反之，对于每个三元有序数组（x，y，z），分别在x轴，y轴和z轴上取坐标为x，y，z的点P，Q，R，然后通过P，Q，R分别作垂直于x轴，y轴和z轴的平面。这三张平面的交点便是由（x，y，z）所确定的唯一的点。这样一来，我们就建立了空间上的点M与三元有序数组（x，y，z）的一一对应关系。称（x，y，z）为点M的坐标，x，y，z称为坐标分量。显然，原点O的坐标为（0，0，0）．由三元有序数组（x，y，z）所确定的点M常记为M（x，y，z）．由于空间上的点与三元有序数组的一一对应关系，在本书中，我们常常将空间上的点与其坐标不加区别。
坐标平面上的点的坐标（x，y，z）有其显著特征。例如，Oxy平面上的点的坐标满足z＝0；Oyz平面上的点的坐标满足x＝0；Ozx平面上的点的坐标满足y＝0．同样地，坐标轴上的点（x，y，z）的坐标也有显著特征。例如，x轴上的点（x，y，z）的坐标满足y＝z＝0；y轴上的点的坐标满足x＝z＝0；z轴上的点的坐标满足x＝y＝0．
设M 1 （x 1 ，y 1 ，z 1 ），M 2 （x 2 ，y 2 ，z 2 ）为空间上两点。过点M 1 和M 2 分别各作三张平面垂直于三个坐标轴，则这六张平面围成一个以线段M 1 M 2 为对角线的长方体（见图6.1.3，这些平面与三个坐标轴的交点如图所示）．
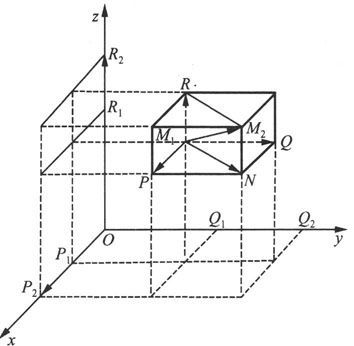
图 6.1.3
M 1 与M 2 的距离d定义为线段M 1 M 2 的长度‖M 1 M 2 ‖．由于
d 2 ＝‖M 1 M 2 ‖ 2 ＝‖M 1 N‖ 2 ＋‖NM 2 ‖ 2
＝‖M 1 P‖ 2 ＋‖PN‖ 2 ＋‖NM 2 ‖ 2
＝‖P 1 P 2 ‖ 2 ＋‖Q 1 Q 2 ‖ 2 ＋‖R 1 R 2 ‖ 2
＝（x 2 －x 1 ） 2 ＋（y 2 －y 1 ） 2 ＋（z 2 －z 1 ） 2 ，
所以
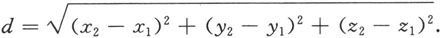
这就是空间中两点间的距离公式。
特别地，如果M 1 和M 2 都在Oxy平面上，则M 1 与M 2 的距离为
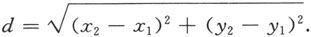
这与平面直角坐标系中的情况相吻合。
显然点M（x，y，z）与原点O（0，0，0）的距离为
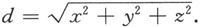
在实际生活中，我们常遇到一类量，如力、速度、加速度等，它们既有大小又有方向。既有大小又有方向的量称为向量。向量通常用黑体字母表示，如a，b，c，x，y，z等。
空间中的向量通常用有向线段表示。所谓有向线段就是规定了一端为起点，另一端为终点，并确定由起点指向终点为方向的线段。有向线段的长度表示向量的大小，方向表示向量的方向。
若向量a与b的大小相等，方向相同，我们就称它们是相等的，记为a＝b．这就是说，如果一个向量通过平行移动，与另一个向量的大小和方向完全重合，我们就认为它们是相等的。
若将向量a或b平行移动使得它们的起点重合后，它们所在射线之间的夹角θ（0≤θ≤π）称为a与b的夹角。
向量a的大小（或长度）用‖a‖表示，它也称为a的模。若‖a‖＝0，则称a为零向量，记为0．零向量没有确定的方向；若‖a‖＝1，则称a为单位向量。
在空间直角坐标系中，对于空间中任一点M，记
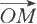为起点为坐标原点O，终点为M的向量，过点M作三张平面分别垂直于x轴，y轴和z轴，它们与这三个轴分别交于P，Q，R三点（见图6.1.2），这三点在x轴，y轴和z轴的坐标为依次为x，y，z，由于MP，MQ和MR分别垂直于坐标轴，因而也分别称x，y和z为
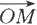在x轴，y轴和z轴上的（数量）投影。由前面的一段的讨论知，
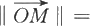
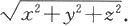显然，向量
与点M是一一对应的，而由
在三个坐标轴上的投影x，y，z组成的三元有序数组（x，y，z）即为点M的坐标。于是，三元有序数组（x，y，z）既可以表示空间中的点M，又可以表示向量
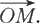进一步，由于我们规定了向量之间的相等关系，对于空间上的任意向量x，我们可以将它平行移动，使它的起点重合于原点，便得到唯一的一个与x相等的向量
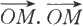在x轴，y轴和z轴上的投影x，y，z称为x在x轴，y轴和z轴上的投影，（x，y，z）称为向量x的坐标，x，y，z称为坐标分量。于是，我们可以将x与（x，y，z）等同起来，即x＝（x，y，z），且显然有
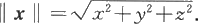这也同时说明，空间向量可以由其坐标唯一确定。在本书中，三元有序数组有时表示空间上的点，有时表示向量，请读者根据不同情况加以确认。
显然，空间中起点为M
1
（x
1
，y
1
，z
1
），终点为M
2
（x
2
，y
2
，z
2
）的向量
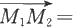（x
2
－x
1
，y
2
－y
1
，z
2
－z
1
），且其长度为
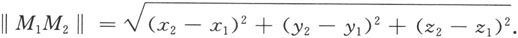
从物理学和力学中我们知道，力可以合成，得到合力。合力遵循平行四边形法则。由此背景出发，我们定义向量的加法如下：
设有向量a，b．任取一点A，作向量
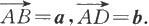记以AB，AD为邻边的平行四边形的对角线为AC，则定义向量
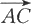为向量a与b的和，记为a＋b（见图6.1.4）．
这个法则也称为平行四边形法则。但此法则对两个相互平行的向量没有说明，因此我们再给出一个更加完善的定义，它称为三角形法则：
设有向量a，b．任取一点A，以A为起点，作向量
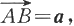再以B为起点作向量
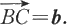则定义向量
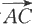为向量a与b的和，记为a＋b（见图6.1.5）．
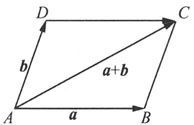
图 6.1.4
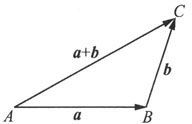
图 6.1.5
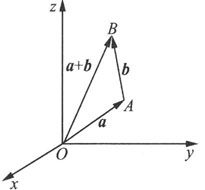
图 6.1.6
下面我们给出向量加法的坐标表达式。
在直角坐标系中，设a＝（x
1
，y
1
，z
1
），b＝（x
2
，y
2
，z
2
）．作
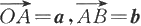（见图6.1.6）．由三角形法则知
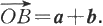设点B的坐标为（x，y，z），因为点A的坐标为（x
1
，y
1
，z
1
），则
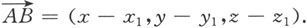
由于向量的坐标是唯一确定的，所以由b＝（x 2 ，y 2 ，z 2 ）得
x 2 ＝x－x 1 ，y 2 ＝y－y 1 ，z 2 ＝z－z 1 ．
即
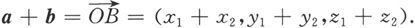
这说明，两个向量之和的坐标分量等于这两个向量的对应坐标分量之和。
设λ是一个实数，a是向量，定义它们的乘积λa是这样一个向量：它的模‖λa‖＝∣λ∣·‖a‖．且当λ＞0时，λa与a的方向相同；当λ＜0时，λa与a的方向相反；当λ＝0时，λa＝0，即λa为零向量。
若向量a与b的夹角为0或π，则称a与b平行。可以证明，两个非零向量a与b平行的充分必要条件是：存在非零实数λ使得a＝λb．
从以上定义易知：若a＝（x，y，z），则λa＝（λ x ，λ y ，λ z ），即，向量与数的乘积的每个坐标分量等于这个向量的对应坐标分量与该数之积。
对于任意向量a，b．定义a－b＝a＋（-1）b．
显然，若a＝（x 1 ，y 1 ，z 1 ），b＝（x 2 ，y 2 ，z 2 ），则
a－b＝（x 1 －x 2 ，y 1 －y 2 ，z 1 －z 2 ）．
从几何上看，a＋b和a－b分别是以a和b为邻边的平行四边形的两条对角线向量。其中a－b的就是以b的终点为起点，以a的终点为终点的向量（见图6.1.7）．
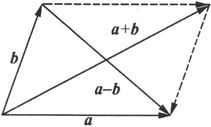
图 6.1.7
很容易验证上面定义的运算满足以下规律，我们此处略去其证明。
定理6.1.1 设a，b，c是向量，λ，μ是实数，则成立
（1）加法交换律：a＋b＝b＋a；
（2）加法结合律：a＋（b＋c）＝（a＋b）＋c；
（3）数乘分配律：λ（a＋b）＝λa＋λb；
（4）数乘结合律：λ（μa）＝（λμ）a．
记空间直角坐标系中与x轴，y轴，z轴同向的单位向量为i，j，k，即
i＝（1，0，0），j＝（0，1，0），k＝（0，0，1）．
那么，对于任意向量a＝（x，y，z）成立
a＝xi＋yj＋zk．
在力学中我们知道，如果一个力F作用于一物体上使它产生位移s，则力F所作的功为
W＝‖F‖‖s‖cosθ，
其中θ是F与s的夹角。我们抽去其物理背景，引入如下概念。
定义6.1.1 设a，b是两个向量，θ为a与b的夹角。则称
‖a‖‖b‖cosθ
为a与b的数量积或内积，记为a·b，即
a·b＝‖a‖‖b‖cosθ．
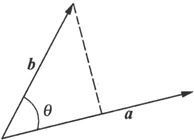
图 6.1.8
我们称‖b‖cosθ为向量b在a方向上的投影。因此，a和b的数量积等于a的模乘以b在a方向上的投影（见图6.1.8）．
若向量a与b的夹角为π/2，则称a与b垂直。从数量积的定义立即推得，两个非零向量a与b垂直的充分必要条件是：a·b＝0．
可以证明数量积满足以下运算规律，我们此处略去其证明。
定理6.1.2 设a，b，c是向量，λ是实数。则
（1）正定性：a·a＝‖a‖ 2 ≥0，且a·a＝0当且仅当a＝0；
（2）交换律：a·b＝b·a；
（3）分配律：（a＋b）·c＝a·c＋b·c；
（4）数乘结合律：（λa）·b＝a·（λb）＝λ（a·b）．
下面我们给出向量数量积的坐标表达式。在直角坐标系中，设a＝（x 1 ，y 1 ，z 1 ），b＝（x 2 ，y 2 ，z 2 ），则由以上运算规律得
a·b＝（x 1 i＋y 1 j＋z 1 k）·（x 2 i＋y 2 j＋z 2 k）
＝x 1 x 2 i·i＋x 1 y 2 i·j＋x 1 z 2 i·k
＋y 1 x 2 j·i＋y 1 y 2 j·j＋y 1 z 2 j·k
＋z 1 x 2 k·i＋z 1 y 2 k·j＋z 1 z 2 k·k．
因为i，j，k是相互垂直的单位向量，则
i·j＝j·i＝0，j·k＝k·j＝0，i·k＝k·i＝0，
i·i＝j·j＝k·k＝1．
于是
a·b＝x 1 x 2 ＋y 1 y 2 ＋z 1 z 2
特别地
a·a＝‖a‖
2
＝
＋
＋
．
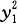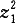记α，β，γ分别为向量a与x轴，y轴和z轴正向的夹角，称cosα，cosβ，cosγ为向量a的方向余弦。若a＝（x 1 ，y 1 ，z 1 ），则显然有
a·i＝x 1 ＝‖a‖cosα，a·j＝y 1 ＝‖a‖cosβ，
a·k＝z 1 ＝‖a‖cosγ．
例6.1.1 设a＝（1，-2，3），b＝（2，3，-1），求a·b以及a与b的夹角θ．
解 由定义得
a·b＝1×2＋（-2）×3＋3×（-1）＝-7．
因为
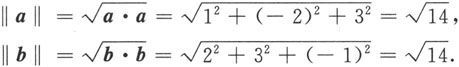
所以
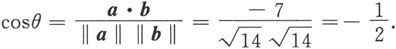
于是
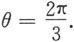
定义6.1.2 设a，b是两个向量，θ为a与b的夹角。定义a与b的向量积或外积a×b是这样一个向量，其模
‖a×b‖＝‖a‖‖b‖sinθ，
其方向与a和b都垂直，且使a，b，a×b符合右手定则。
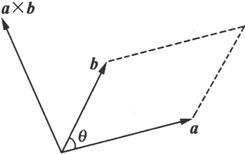
图 6.1.9
a，b，a×b符合右手定则是指：伸平右手，先用除拇指外的四指指向a方向，再顺势向b方向弯曲，则拇指所指的方向就是a×b的方向（见图6.1.9）．
由定义，a×b垂直于a和b所确定的平面，且‖a×b‖＝‖a‖‖b‖sinθ说明向量a×b的模等于以a和b为邻边的平行四边形的面积。
对于任何向量a，显然成立a×a＝0．进一步由定义可知，两个非零向量a与b平行的充分必要条件是：a×b＝0．
可以证明向量积满足以下运算规律，我们此处略去其证明。
定理6.1.3 设a，b，c是向量，λ是实数。则
（1）反交换律：a×b＝-b×a；
（2）分配律：（a＋b）×c＝a×c＋b×c；
（3）数乘结合律：（λa）×b＝a×（λb）＝λ（a×b）．
下面我们给出向量数量积的坐标表达式。在直角坐标系中，设a＝（x 1 ，y 1 ，z 1 ），b＝（x 2 ，y 2 ，z 2 ），则由以上运算规律得
a×b＝（x 1 i＋y 1 j＋z 1 k）×（x 2 i＋y 2 j＋z 2 k）
＝x 1 x 2 i×i＋x 1 y 2 i×j＋x 1 z 2 i×k
＋y 1 x 2 j×i＋y 1 y 2 j×j＋y 1 z 2 j×k
＋z 1 x 2 k×i＋z 1 y 2 k×j＋z 1 z 2 k×k．
因为
i×i＝j×j＝k×k＝0，
以及
i×j＝k，j×k＝i，k×i＝j，
j×i＝-k，k×j＝-i，i×k＝-j，
于是
a×b＝（y 1 z 2 －z 1 y 2 ）i＋（z 1 x 2 －x 1 z 2 ）j＋（x 1 y 2 －y 1 x 2 ）k．
它也可以写为
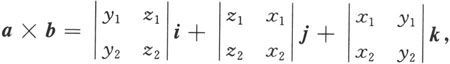
或用三阶行列式形式地表为
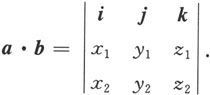
例6.1.2 确定单位向量c，使得c与向量a＝（1，3，5），b＝（3，2，4）都垂直。
解 因为a×b与a和b都垂直，所以c与a×b平行，且‖c‖＝1．因此
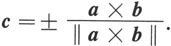
由于
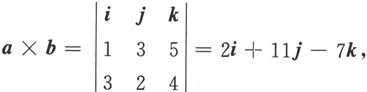
以及
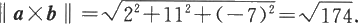
所以
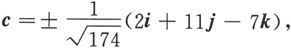
即
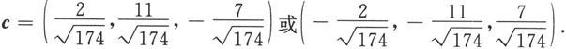
在我们日常生活中，经常会看到各种各样的曲面。例如，足球的表面、汽车灯的反射面、灯管的表面、漏斗的内表面等。曲面可以看成满足一定条件的动点的轨迹，在空间直角坐标系中，动点满足的条件可以用以动点坐标（x，y，z）为变量的三元方程表示。
定义6.1.3 若空间中的曲面∑上的任意一点的坐标（x，y，z）都满足方程F（x，y，z）＝0；同时，坐标满足方程F（x，y，z）＝0的点都在曲面∑上，则称
F（x，y，z）＝0
是曲面∑的轨迹方程，简称为曲面方程。称曲面∑的几何图形为方程F（x，y，z）＝0的图形。
空间曲线也是动点的轨迹，位于曲线上的点的坐标（x，y，z）也满足一定的方程。一般地，一条空间曲线可以看成两个不同曲面的交线。
与平面解析几何类似，对空间曲面的研究有两个基本问题，一个是知道曲面上的点的变化规律，求相应的轨迹方程，即曲面方程；另一个问题是，已经知道方程F（x，y，z）＝0，求相应曲面的几何形状。
例6.1.3 求以点P 0 （x 0 ，y 0 ，z 0 ）为中心，半径为r的球面的方程。
解 设P（x，y，z）是球面上的任意一点，则∣PP 0 ∣＝r，即
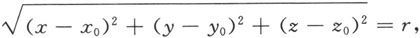
因此，所求的球面方程是
（x－x 0 ） 2 ＋（y－y 0 ） 2 ＋（z－z 0 ） 2 ＝r 2
于是，中心为原点，半径为r的球面方程是
x 2 ＋y 2 ＋z 2 ＝r 2 ．
例6.1.4 求x 2 ＋y 2 ＋z 2 ＋4x－2y－10z－6＝0表示的曲面。
解 所给的方程的左端配方，并移项得
（x＋2） 2 ＋（y－1） 2 ＋（z－5） 2 ＝36．
因此方程表示的是以（-2，1，5）为中心，半径为6的球面。
例6.1.5 求与两点P 1 （1，-1，2）和P 2 （2，0，1）等距离的点P的轨迹方程。
解 设P（x，y，z）是轨迹上的任意一点，则∣PP 1 ∣＝∣PP 2 ∣，即
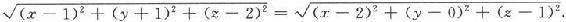
将其整理得到
2x＋2y－2z＋1＝0．
这就是点P的轨迹方程。由立体几何知，P的轨迹就是线段P 1 P 2 的垂直平分面。
显然，方程z＝0确定的平面就是Oxy平面，更一般地，方程z＝k确定的平面就是过点（0，0，k）且与Oxy平面平行的平面。它们都与z轴垂直。
在空间中，若已知与平面垂直的一个方向和平面上的一个点，就可以唯一决定这个平面。与一个平面垂直的非零向量称为这个平面的法向量。
设平面π的法向量为n＝（A，B，C）（A，B，C不同时为零），而且该平面通过点P
0
（x
0
，y
0
，z
0
）．设P（x，y，z）为平面上的任何一点，则从P到P
0
的线段属于平面π，因而向量
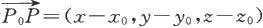与n垂直，所以
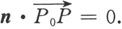
即
A（x－x 0 ）＋B（y－y 0 ）＋C（z－z 0 ）＝0．
这就是说，平面π上的点都满足以上方程。显然，不在平面π上的点不满足以上方程。因此上述关系式就是平面π的方程。它称为平面的点法式方程。
记常数D＝-（Ax 0 ＋By 0 ＋Cz 0 ），则上述方程可以写成
Ax＋By＋Cz＋D＝0，
这个关系式称为平面的一般方程。
例6.1.6 求法向量为（1，-2，3），且过点（3，4，-5）的平面方程。
解 由点法式方程得所求平面的方程为
（x－3）－2（y－4）＋3（z＋5）＝0，
即
x－2y＋3z＋20＝0．
例6.1.7 求过三点P 1 （a，0，0），P 2 （0，b，0），P 3 （0，0，c）的平面的方程，其中a，b，c为非零常数（见图6.1.10）．
解 设平面方程为
Ax＋By＋Cz＋D＝0．
因为平面过P 1 ，P 2 和P 3 点，所以这些点的坐标满足平面方程。于是
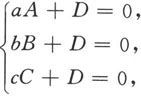
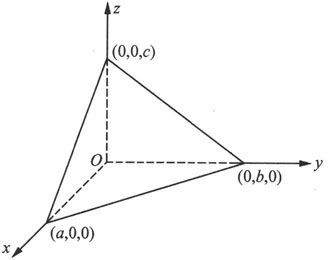
图 6.1.10
所以
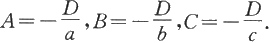代入原方程并化简得
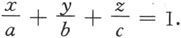
这种方程称为平面的截距式方程，a，b，c依次称为平面在x轴，y轴，z轴上的截距。
我们知道，一个圆绕过其圆心的直线旋转一周的轨迹就是球面。更一般地，我们引入如下定义。
定义6.1.4 由一条定曲线绕一条定直线旋转一周而生成的曲面称为旋转曲面。
已知Oyz平面上的一条曲线，其方程为
f（y，z）＝0．
把它绕z轴旋转一周，就生成一个旋转曲面，其方程可如下求得：
设点P 0 （0，y 0 ，z 0 ）是旋转曲面在Oyz平面上的点，因此
f（y 0 ，z 0 ）＝0．
曲线绕z轴旋转，当该点转到位置P（x，y，z）时，显然有（见图6.1.11）
z＝z 0 ，
而P到z轴的距离与P 0 到z轴的距离相等，即
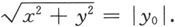
代入曲线方程，就得到P（x，y，z）满足
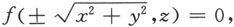
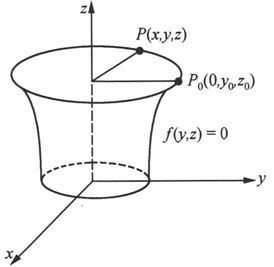
图 6.1.11
这就是f（y，z）＝0绕z轴旋转一周生成的旋转曲面的方程。
完全类似地可以导出，该曲线绕y轴旋转一周生成曲面的方程为
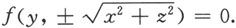
读者不难推出在Oxy面上的曲线
g（x，y）＝0
分别绕x轴和y轴旋转一周生成的旋转曲面的方程以及Ozx平面上的曲线
h（x，z）＝0
分别绕x轴和z轴旋转一周生成的旋转曲面的方程。
例6.1.8 求Oyz平面上的抛物线z 2 ＝y绕y轴旋转一周而生成的旋转曲面的方程。
解 绕y轴旋转一周而生成的旋转曲面的方程为
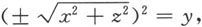
即
y＝x 2 ＋z 2 ．
这种曲面称为旋转抛物面（见图6.1.12）
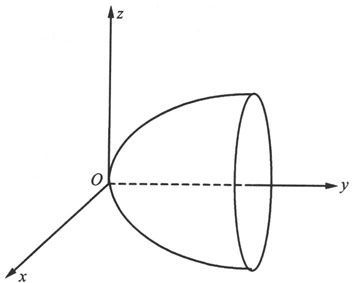
图 6.1.12
我们先看一个例子。
例6.1.9 求y＝x 2 表示的曲面。
解 在Oxy平面上中，这是一条抛物线。现在考虑在空间上的情况。设Oxy平面上的点P（x 0 ，y 0 ，0）在抛物线上，即满足
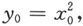
由于方程y＝x 2 中不含变量z，因此，对任意z，（x 0 ，y 0 ，z）一定也满足方程，所以该点也在y＝x 2 所表示的曲面上。
这就是说，若过P 0 作一条垂直于Oxy平面（即与z轴平行）的直线，由于这条直线上的任意一点的坐标为（x 0 ，y 0 ，z），那么这条直线包含于y＝x 2 所表示的曲面中。取遍抛物线上所有的点，即这条直线沿抛物线平行移动，就得到了y＝x 2 表示的曲面（见图6.1.13），它称为抛物柱面。
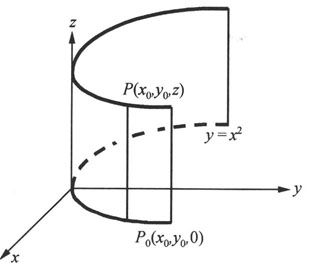
图 6.1.13
定义6.1.5 若给定一条曲线C和一条直线L，平行于L的直线L c 沿曲线C移动所形成的曲面称为柱面，定曲线C称为柱面的准线，动直线L c 称为柱面的母线。
显然，平面是一种特殊的柱面：它的准线通常取作一条直线。
不含z的方程f（x，y）＝0表示以Oxy平面上的曲线f（x，y）＝0为准线，母线平行于z轴的柱面。例如，曲面x
2
＋y
2
＝1是以Oxy平面上的单位圆为准线，母线平行于z轴的圆柱面（见图6.1.14）；曲面
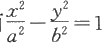是以Oxy平面上的双曲线为准线，母线平行于z轴的双曲柱面（见图6.1.15）．而曲面x＋y＝0是以Oxy平面上的直线为准线，母线平行于z轴的柱面，即平面（见图6.1.16）．
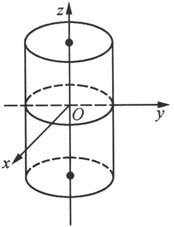
图 6.1.14
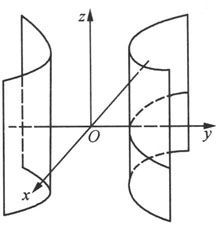
图 6.1.15
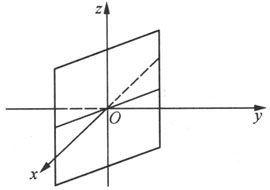
图 6.1.16
我们已经知道空间的一条曲线可以看成是两个曲面的交线。若这两个曲面的方程分别为F（x，y，z）＝0和G（x，y，z）＝0，那么曲线方程可以表示为
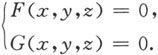
这种关系式称为曲线的一般方程。
例如，在空间中抛物柱面y＝x 2 是曲面，而不是曲线，抛物柱面与Oxy坐标平面的交线，即方程
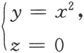
表示的曲线才是一条抛物线。
例6.1.10 方程
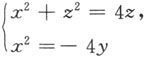
表示的曲线是圆柱面x 2 ＋z 2 ＝4z与抛物柱面x 2 ＝-4y的交线（见图6.1.17）．
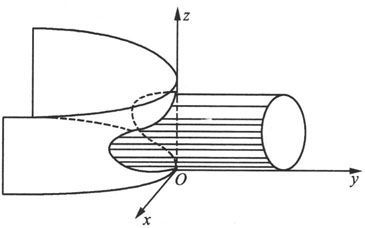
图 6.1.17
例6.1.11 说明方程
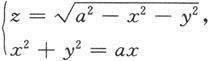
表示的曲线。
解 方程
是以原点为球心，a为半径的球面的上半部分，而x
2
＋y
2
＝ax是以Oxy平面上的圆
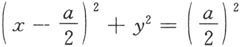
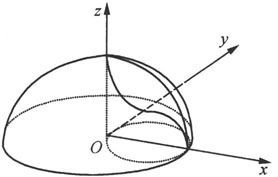
图 6.1.18
为准线，母线平行于z轴的圆柱面。它们的交线如图6.1.18所示。
两张不平行的平面的交线就是直线。在空间中，若已知与直线的平行的一个方向和直线上的一个点，就可以唯一决定这条直线。平行于一条直线的非零向量称为该直线的方向向量。
设直线L的方向向量为ι＝（ι，m，n）（ι，m，n不全为零），且该直线通过点P
0
（x
0
，y
0
，z
0
）．设P（x，y，z）为直线L上的任何一点，则向量
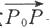与ι平行（见图6.1.19），从而存在实数t使得
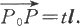按坐标表示就是
（x－x 0 ，y－y 0 ，z－z 0 ）＝t（ι，m，n），
即
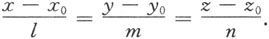
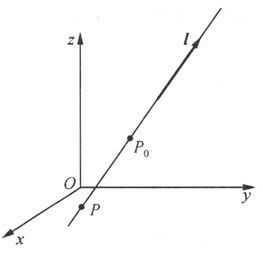
图 6.1.19
显然，不在直线上的点不满足以上方程。因此上述关系式就是直线L的方程，它称为直线的对称式方程（或点向式方程）．
注意，若ι，m，n中有某个等于0，则它对应的分子应理解为0．例如ι＝0，则关系式
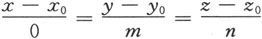
则应理解为
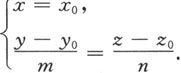
若已知直线L通过两个点P
0
（x
0
，y
0
，z
0
）和P
1
（x
1
，y
1
，z
1
），则
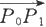
就是该直线的方向向量（见图6.1.20），代入直线的对称式方程，便得到直线L的两点式方程
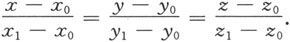
例6.1.12 求过点P 0 （1，1，-1）和P 1 （2，5，-7）的直线方程。
解 因为
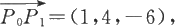所以所求的直线方程为
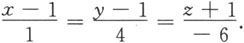
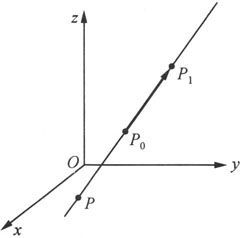
图 6.1.20
例6.1.13 用对称式方程表示直线
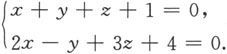
解 显然，方程组中的第一个方程表示的平面的一个法向量为n 1 ＝（1，1），方程组中的第二个方程表示的平面的一个法向量为n 2 ＝（2，-1，3）．因为方程组所表示的直线在这两张平面上，因此该直线的方向向量必与n 1 和n 2 垂直。于是可取直线的一个方向向量为
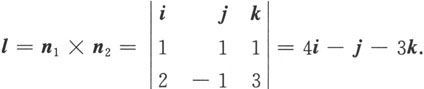
再在两张平面上任意找一个公共点（即直线上一点）．例如，令x 0 ＝0，代入方程组得
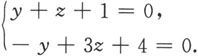
从而可以解出
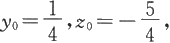即
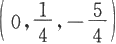为直线上一点。于是直线的对称式方程为
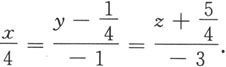
空间曲线还有一种常用的表示方式。设x（t），y（t），z（t）是［α，β］上的连续函数，那么对于固定的t 0 ，（x（t 0 ），y（t 0 ），z（t 0 ）），就确定了空间中的一个点，当t从α连续地变化到β时，点（x（t），y（t），z（t））的轨迹就是空间中的一条连续曲线。因此关系式
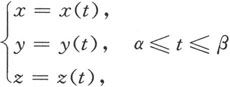
也表示了一条空间曲线，称为曲线的参数方程。曲线的参数方程对于求解某些具体问题很有效。
若在直线的对称式方程中令
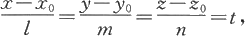将这个等式写开，就得到
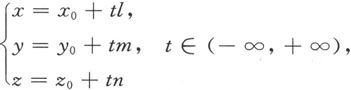
这称为直线的参数方程。
例6.1.14 求直线
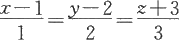与平面x＋2y－3z－2＝0的交点。
解 该问题就是求方程
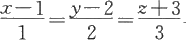与x＋2y－3z－2＝0的公共解。
先将直线方程写成参数方程
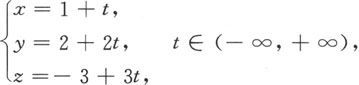
将其代入平面的方程，便得到
（1＋t）＋2（2＋2t）－3（-3＋3t）－2＝0，
解得t＝3．再代入直线的参数方程，得到
x＝4，y＝8，z＝6，
即，交点为（4，8，6）．
例6.1.15 说明参数方程
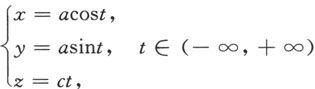
表示的曲线，其中a＞0，c＞0．
解 先考虑c＝0的特殊情况，当t连续地增大时，曲线在Oxy平面上逆时针连续地画出圆心在原点，半径为a的重叠的圆。
对一般的c＞0，易知当t连续地增大时，曲线上的点按速度c匀速地上升。
将上面两点综合起来，就得到了方程表示的曲线（见图6.1.21），这条曲线称为螺旋线，旋转一周后z增加的高度2cπ称为螺距。
日常生活中用的平头螺钉上的螺纹就是一条螺旋线，用螺丝刀每旋紧一周，螺钉就往里移进一个螺距的长度。
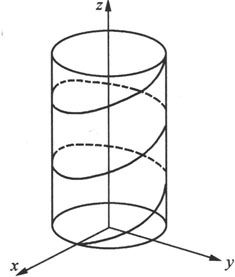
图 6.1.21
在空间直角坐标系中，由三元二次方程
a 11 x 2 ＋a 22 y 2 ＋a 33 z 2 ＋2a 12 xy＋2a 13 xz＋2a 23 yz＋b 1 x＋b 2 y＋b 3 z＋c＝0确定的曲面称为二次曲面。二次曲面在曲面理论中占有重要地位，这不仅在于它们的形状比较简单，极为常用，而且在于许多复杂的曲面在一定的条件下可以用它们近似代替。
可以证明，经过适当的坐标变换，可以使得二次曲面的方程中不含交叉项（即两个不同变量的乘积项），并且不同时含有某个变量的一次项和二次项，这类方程称为二次曲面的标准方程。
下面就二次曲面的标准方程对几个典型的二次曲面的形状作一简单的介绍。讨论的方法是用坐标平面及一些特殊的平面与二次曲面相截，考察其截痕（曲线）的形状，然后对截痕加以综合，进而得出曲面的全貌，这种方法称为截痕法。
一般的椭球面方程为
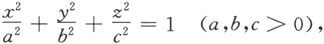
利用截痕法，我们用平面z＝z 0 （∣z 0 ∣＜c）去截它，得曲线
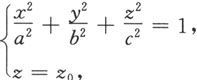
从方程中消去z，便得到
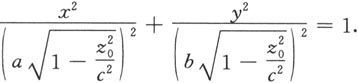
这是平面z＝z
0
上的以点（0，0，z
0
）为中心，两个半轴分别为
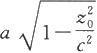和
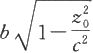的椭圆，当z
0
→c时，椭圆收缩为一个点。
对x和y方向作类似的讨论，不难得到椭球面的图形（见图6.1.22）．其中，（±a，0，0），（0，±b，0），（0，0，±c）称为椭球面的顶点，a，b，c称为椭球的半轴。
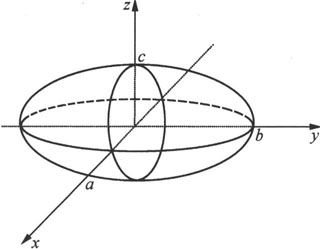
图 6.1.22
当a＝b＝c时，椭球面方程就变为球面方程
x 2 ＋y 2 ＋z 2 ＝a 2 ．
1．单叶双曲面
一般的单叶双曲面方程为
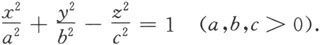
我们在两个方向上用截痕法讨论这个曲面。先用平面z＝z 0 去截，得曲线
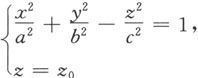
从方程中消去z，便得到
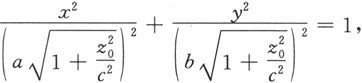
这是平面z＝z
0
上以（0，0，z
0
）为中心，两个半轴分别为
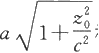和
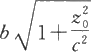的椭圆，当z
0
＝0时椭圆最小，它的两个半轴分别为a和b，当z
0
→±∞时，椭圆的半轴趋向于无穷大。
再用平面y＝y 0 去截，得曲线
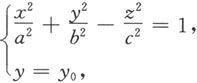
从方程中消去y，便得到：
（1）当∣y 0 ∣＜b时，
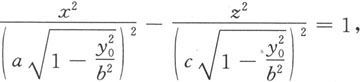
这是平面y＝y 0 上以（0，y 0 ，0）为中心，实轴与x轴平行，虚轴与z轴平行的双曲线。
（2）当∣y 0 ∣＞b时，
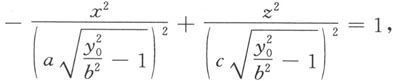
这是平面y＝y 0 上以（0，y 0 ，0）为中心，实轴与z轴平行，虚轴与x轴平行的双曲线。
（3）当∣y 0 ∣＝b时，
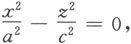
这是在平面y＝b（y＝-b）上一对相交于（0，b，0）（（0，-b，0））点，且关于z轴对称的直线。
对x方向的讨论与y方向的讨论是类似的。于是得到单叶双曲面的图形（见图6.1.23）．
2．双叶双曲面
一般的双叶双曲面方程为
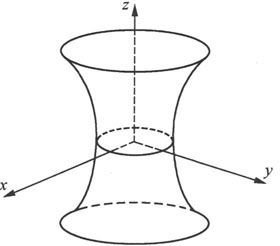
图 6.1.23
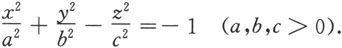
与单叶双曲面方程的讨论类似，双叶双曲面的图形见图6.1.24．
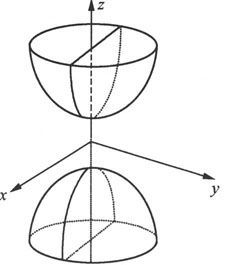
图 6.1.24
图 6.1.25
3．锥面
一般的二次锥面方程为
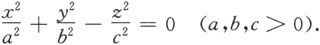
它可以看成是双曲面（无论是单叶还是双叶）的极限情况，其图形如图6.1.25所示，讨论的过程请读者自己完成。
1．椭圆抛物面
一般的椭圆抛物面方程为
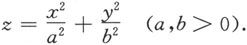
用平面z＝z 0 （z 0 ＞0）去截，得曲线
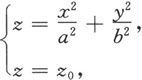
消去z，便得到
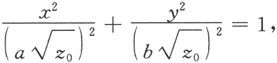
这是平面z＝z
0
上以（0，0，z
0
）为中心，两个半轴分别为
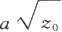和
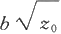的椭圆。
当z 0 →0时，椭圆收缩于一个点。
再用平面y＝y 0 去截，得曲线
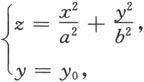
消去y，便得到
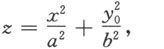
这是平面y＝y
0
上以
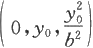为顶点，对称轴与z轴平行的一条抛物线，抛物线的顶点的轨迹是Oyz平面上的抛物线
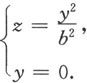
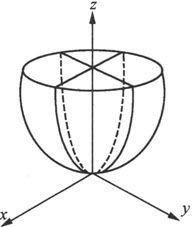
图 6.1.26
对x方向作类似的讨论，就得到椭圆抛物面的图形（见图6.1.26）．
2．双曲抛物面
双曲抛物面的标准方程为
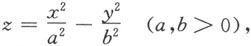
同样地，可利用截痕法研究这个曲面，在此不再详述，其图形见图6.1.27，它被形象地称为马鞍面。
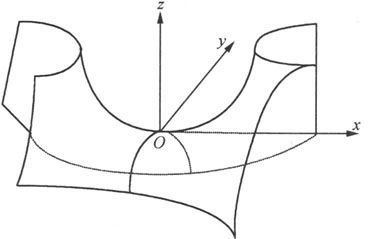
图 6.1.27