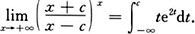1.根据定义计算定积分
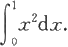
2.举出函数f和g在[a,b]上都连续,但下式不成立的例子。
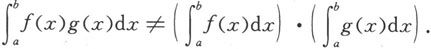
3.判断下列积分的大小:
(1)
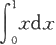 和
和
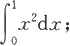
(2)
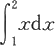 和
和
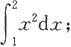
(3)
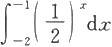 和
和
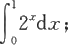
(4)
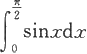 和
和
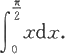
4.求下列函数的导数:

5.求下列极限:
(1)
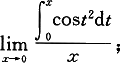
(2)
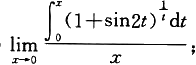
(3)
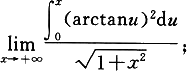
(4)
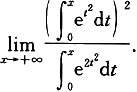
6.利用积分中值定理求下列极限:
(1)
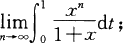
(2)
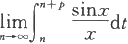 (p是正整数).
(p是正整数).
7.求下列定积分:


8.求函数
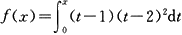 的极值。
的极值。
9.设函数f在(0,+∞)上连续,且满足
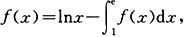 求
求
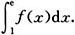
10.设函数
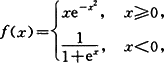 计算定积分
计算定积分
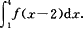
11.设f是(-∞,+∞)上以T为周期的连续函数。证明:对于任何实数a下式成立
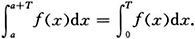
12.求下列曲线所围平面图形的面积:
(1)
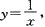 y=x,x=2;
y=x,x=2;
(2)y 2 =4(x+1),y 2 =4(1-x);
(3)y=x,y=x+sin 2 x,x=0,x=π;
(4)y=e x ,y=e -x ,x=1;
(5)阿基米德螺线r=aθ,θ=0,θ=2π;
(6)蚌线r=acosθ+b(b≥a>0);
(7)r=3cosθ,
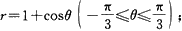
(8)双纽线r 2 =a 2 cos2θ.
13.求函数y=x 3 -3x+2的极大值点x 1 和极小值点x 2 ,并求该函数的图形与直线x=x 1 ,x=x 2 以及x轴所围图形的面积。
14.求上底是长半轴为a、短半轴为b的椭圆,下底是长半轴为A、短半轴为B的椭圆(A>a,B>b),高为h的正椭圆台的体积。
15.求下列平面图形分别绕x轴、y轴旋转一周形成的旋转体的体积:
(1)曲线
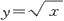 与直线x=1,x=4,y=0所围图形;
与直线x=1,x=4,y=0所围图形;
(2)曲线
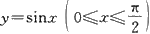 与直线
与直线
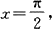 y=0所围图形;
y=0所围图形;
(3)曲线y=x 3 与直线x=2,y=0所围图形;
(4)曲线x
2
+y
2
=1与
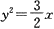 所围的两个图形之中面积较小的一块。
所围的两个图形之中面积较小的一块。
16.记V(ξ)是曲线
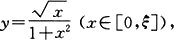 直线x=ξ及x轴所围图形绕x轴旋转一周所成旋转体的体积,求常数a使得
直线x=ξ及x轴所围图形绕x轴旋转一周所成旋转体的体积,求常数a使得
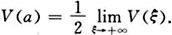
17.已知某产品的边际收益函数为
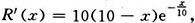
其中x为销售量,求收益函数R(x).
18.已知某产品的边际成本和边际收益函数分别为
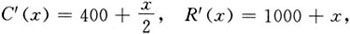
其中x为销售量(单位:台).求生产多少台产品时总利润最大,并求当总利润最大时总收入是多少?
19.已知一笔投资连续3年内保持收入15000元不变。若假设利率为7.5%的连续复利计息,问收入的现值是多少?
20.计算下列无限区间上的广义积分(发散也是一种计算结果):
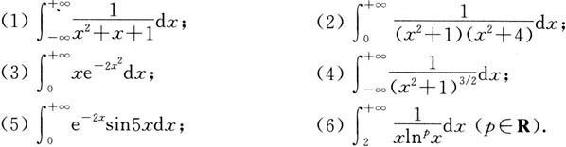
21.计算下列无界函数的广义积分(发散也是一种计算结果):

22.讨论下列广义积分的敛散性:
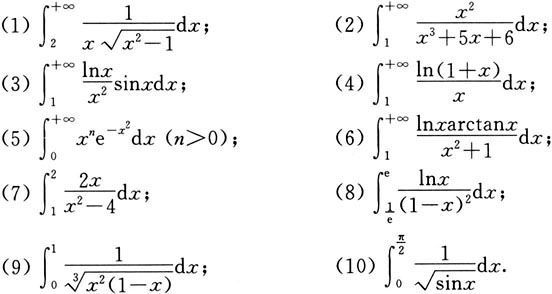
23.利用Γ函数和B函数的性质计算:
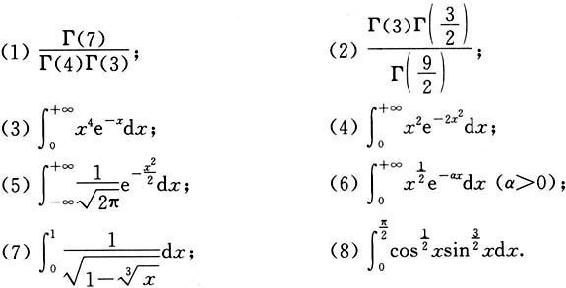
1.设函数f在[a,b]上连续、非负,但不恒为0,证明
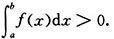
2.设函数f在[0,1]上连续,且单调减少,证明对任意a∈[0,1],成立
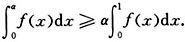
3.设函数f和g在[a,b]上都可积,证明施瓦茨(Schwarz)不等式
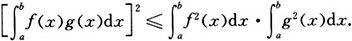
4.设f是[0,+∞)上的连续函数,且恒有f(x)>0,证明函数g(x)=
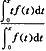 是[0,+∞)上的单调增加函数。
是[0,+∞)上的单调增加函数。
5.设函数
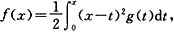 其中函数g在(-∞,+∞)上连续,且g(1)=5,
其中函数g在(-∞,+∞)上连续,且g(1)=5,
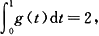 证明
证明
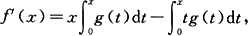 并计算f″(1)和f
并计算f″(1)和f
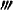 (1).
(1).
6.设函数f连续,且满足
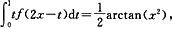 f(1)=1.求
f(1)=1.求
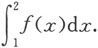
7.设函数
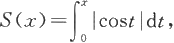 求极限
求极限
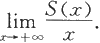
8.设函数f在(-∞,+∞)上连续,证明
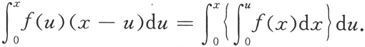
9.设函数f在[0,1]上二阶可导,且在[0,1]上成立f″(x)≤0.证明:
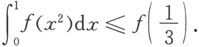
10.设函数f在[0,π]上连续,且
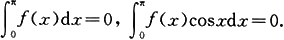 证明:在(0,π)内至少存在两个不同的点ξ
1
,ξ
2
,使得f(ξ
1
)=f(ξ
2
)=0.
证明:在(0,π)内至少存在两个不同的点ξ
1
,ξ
2
,使得f(ξ
1
)=f(ξ
2
)=0.
11.求曲线x 4 +y 4 =a 2 (x 2 +y 2 )所围平面图形的面积。
12.求c的值,使得