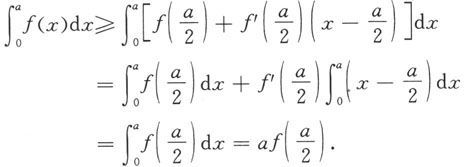例5.6.1 计算
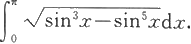
解 因为当x∈[0,π]时,
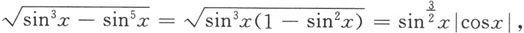
而
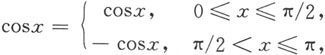
所以
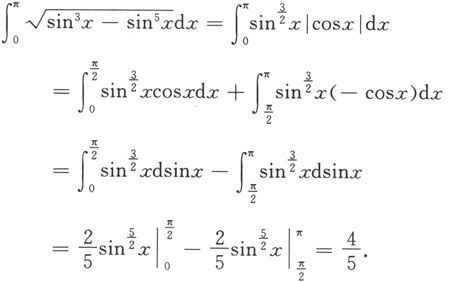
例5.6.2 设函数f在(-∞,+∞)上连续,计算
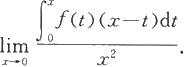
解 因为
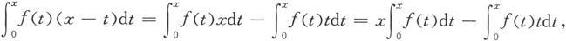
所以
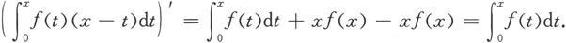
于是由洛必达法则得
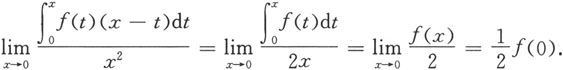
例5.6.3 计算
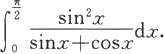
解 作变量代换
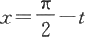 便得
便得
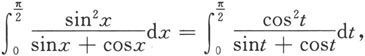
因此
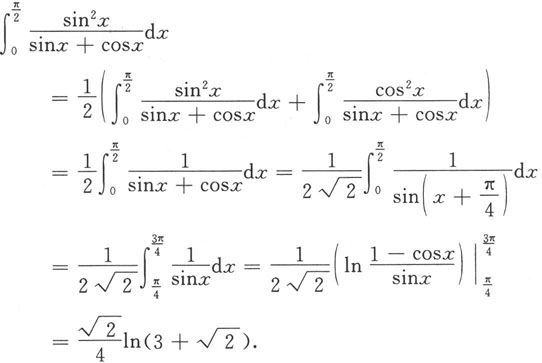
例5.6.4 设
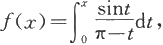 求
求
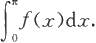
解 易知
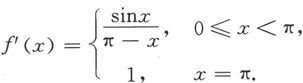
它在[0,π]上连续。由分部积分法得
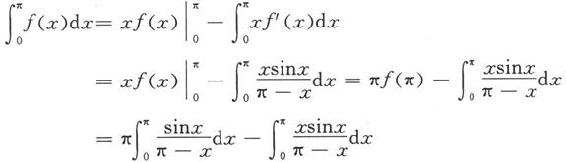
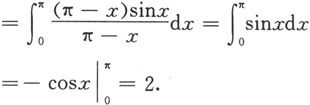
例5.6.5 计算
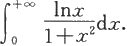
解 因为
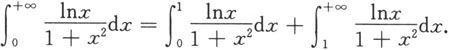
对等式右端第二个积分作变量代换
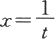 得
得
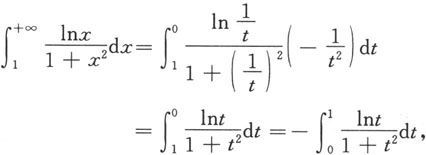
所以
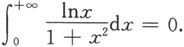
例5.6.6 设直线y=ax(0<a<1)与抛物线y=x 2 所围成的图形的面积为S 1 ,且它们与直线x=1所围成图形的面积为S 2 .
(1)确定a的值,使得S 1 +S 2 达到最小,并求出最小值;
(2)求该最小值所对应的平面图形绕x轴旋转一周所得旋转体的体积。
解 (1)显然直线y=ax(0<a<1)与抛物线y=x 2 的交点为(a,a 2 ),所以
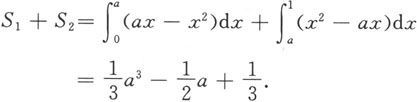
记
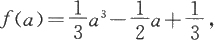 则
则
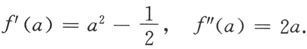
令f′(a)=0得
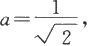 且
且
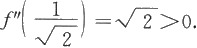 所以
所以
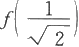 为极小值,它是唯一的极值,因此也是最小值。这说明S
1
+S
2
在
为极小值,它是唯一的极值,因此也是最小值。这说明S
1
+S
2
在
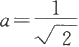 点取到最小值
点取到最小值
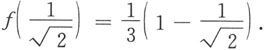
(2)对于任意a∈(0,1),平面图形绕x轴旋转一周所得旋转体的体积为
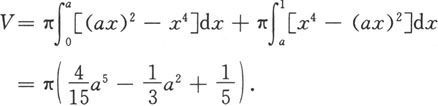
将
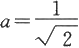 代入上式便得使S
1
+S
2
达到最小值时,所对应的平面图形绕x轴旋转一周所得旋转体的体积
代入上式便得使S
1
+S
2
达到最小值时,所对应的平面图形绕x轴旋转一周所得旋转体的体积
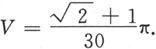
例5.6.7 设函数f在[a,b]上连续,在(a,b)上可导,且满足
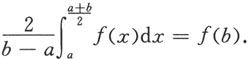
证明:存在ξ∈(a,b),使得f′(ξ)=0.
证 由积分中值定理知,存在
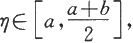 使得
使得
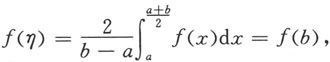
再对f在[η,b]上应用罗尔定理便知,存在ξ∈(η,b)⊂(a,b),使得f′(ξ)=0.
证毕
例5.6.8 设函数f在[0,a]上二阶可导(a>0),且f″(x)≥0,证明:
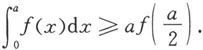
证 函数f在
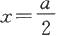 点的一阶泰勒公式为
点的一阶泰勒公式为
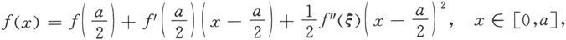
其中0<ξ<a.由于在[0,a]上成立f″(x)≥0,所以
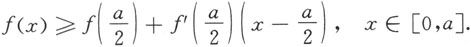
将上述不等式两边从0到a积分,注意到
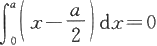 便得
便得