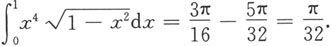由牛顿-莱布尼茨公式可知,要计算定积分,只要求出被积函数的一个原函数,再将定积分的上、下限代入该原函数即可。如果被积函数比较复杂,自然可以利用不定积分的换元法和分部积分法求出它的原函数,再将定积分的上、下限代入便可计算出定积分的值。然而,在许多理论和实际问题中,还需要直接利用定积分的换元积分法和分部积分法。
定理5.3.1 设函数f(x)在区间[a,b]上连续,函数x=φ(t)在区间[α,β](或区间[β,α])上有连续导数,满足φ(α)=a和φ(β)=b,且函数φ的值域包含于[a,b].则成立
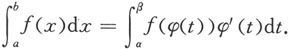
证 因为函数f在区间[a,b]上连续,所以必有原函数。设F为f在区间[a,b]上的一个原函数,由复合函数求导法则可知
[F(φ(t))]′=F′(φ(t))φ′(t)=f(φ(t))φ′(t),
因此F(φ(t))是f(φ(t))φ′(t)一个原函数。由牛顿-莱布尼茨公式便得
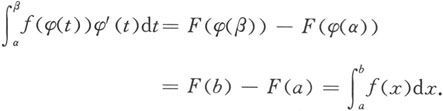
证毕
注意,换元后的定积分
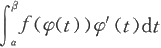 的上下限α和β必须与原定积分的上下限a和b相对应,而不必考虑α与β之间的大小。
的上下限α和β必须与原定积分的上下限a和b相对应,而不必考虑α与β之间的大小。
例5.3.1 算定积分
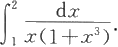
解法一 令
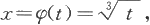 则
则
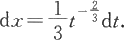 因为φ(1)=1,φ(8)=2,积分区间x∈[1,2]对应于t∈[1,8].应用换元积分公式便得到
因为φ(1)=1,φ(8)=2,积分区间x∈[1,2]对应于t∈[1,8].应用换元积分公式便得到
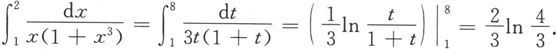
解法二 易知
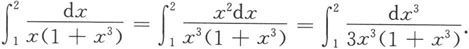
令u=ψ(x)=x 3 ,则ψ(1)=1,ψ(2)=8,于是由换元积分公式得
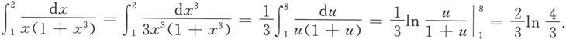
从上例可以看出,换元积分公式
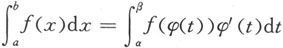
可以从左端推到右端,也可以从右端推到左端。解法一就是采用从左端推到右端的方法,这相当于不定积分的第二类换元积分法;解法二则是采用从右端推到左端的方法,这相当于不定积分的第一类换元积分法,即“凑微分法”.读者应该对具体的问题作具体的分析,选择恰当的变量代换,从而简化计算过程。
例5.3.2 求半径为a的圆的面积。
解 设圆的方程为
x 2 +y 2 =a 2 ,
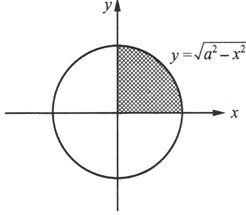
图5.3.1
利用对称性,我们只需求它在第一象限部分的面积,其4倍就是整个圆的面积。
在第一象限,圆的方程可变为
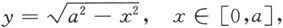
因此,相应的四分之一圆面积为
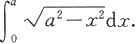
为计算这个积分,作变量代换x=asint,于是dx=acostdt,积分区间x∈[0,a]对应于
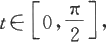 于是
于是
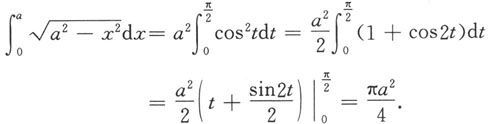
所以,整个圆的面积为S=πa 2 .
例5.3.3 计算定积分

解 作变量代换
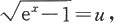 则x=ln(1+u
2
),所以
则x=ln(1+u
2
),所以
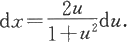 由于当x=0时,u=0;当x=ln2时,u=1,于是
由于当x=0时,u=0;当x=ln2时,u=1,于是
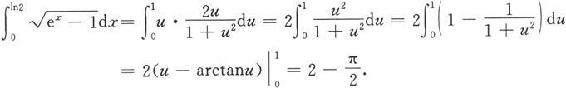
要补充说明的是,如果在计算中使用的是“凑微分”的换元法,在计算过程往往不必另行写出中间变量,因而也毋须引入中间变量的变化区间。这就是说,如果F(u)是f(u)的原函数,φ(x)在[a,b]上具有连续导数,且φ的值域包含于f的定义域,则
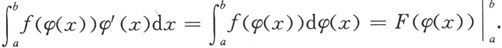
例5.3.4 计算
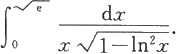
解 利用“凑微分”法得
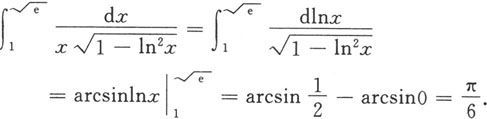
定理5.3.2 设函数f在对称区间[-a,a]上连续,则
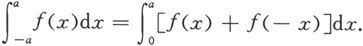
从而
(1)若f是偶函数,则
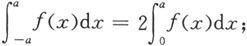
(2)若f是奇函数,则
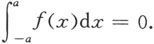
证 由于
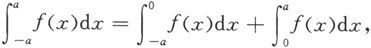
对积分
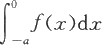 作变量代换x=-t得
作变量代换x=-t得
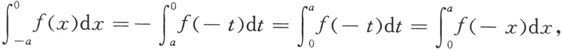
于是
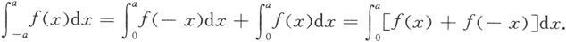
证毕
这个定理中的结论(1)和(2)的几何意义是非常明显的,并且它们可使定积分的计算更为简单。例如,从结论(2)立刻可知
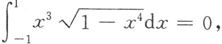
这是因为被积函数是奇函数。
例5.3.5 计算
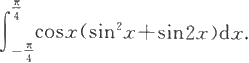
解 因为cosxsin 2 x是偶函数,cosxsin2x是奇函数,由定理5.3.2得
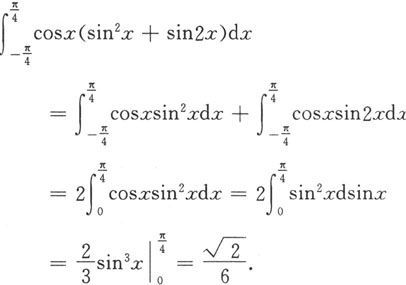
例5.3.6 计算定积分
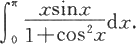
解 由定积分的区间可加性得
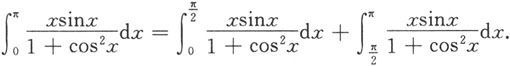
对等式右边的第二个积分作变量代换x=π-t得
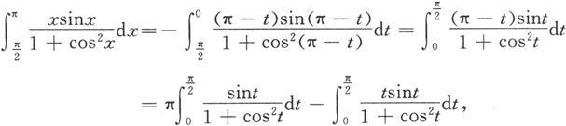
于是
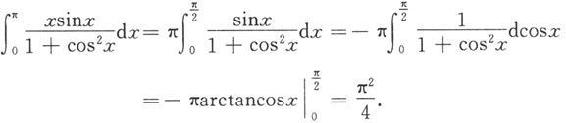
注意,在本题中我们实际上并没有求出函数
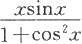 的原函数,只是利用换元积分法把不易计算的部分消去了。因此定积分换元法的使用是有其自身特点的,不要简单地认为它与不定积分的换元法的作用相同。
的原函数,只是利用换元积分法把不易计算的部分消去了。因此定积分换元法的使用是有其自身特点的,不要简单地认为它与不定积分的换元法的作用相同。
设函数u和v在区间[a,b]上有连续导数。由函数乘积的求导公式
(uv)′=uv′+vu′
可得
uv′=(uv)′-vu′.
将上式在[a,b]上取定积分便得
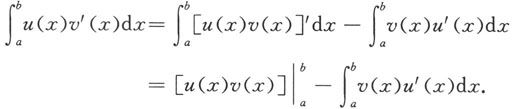
这样便有如下的分部积分公式:
定理5.3.3 设函数u和v在[a,b]上有连续导数,则
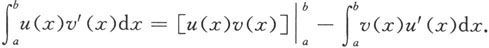
上式也可表成下列形式
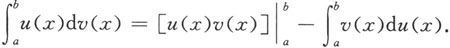
例5.3.7 计算定积分
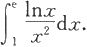
解 应用分部积分公式得
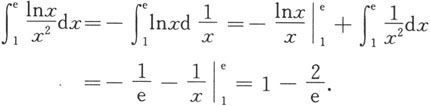
例5.3.8 计算定积分
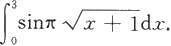
解 作变量代换
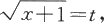 则x=t
2
-1,dx=2tdt,所以
则x=t
2
-1,dx=2tdt,所以
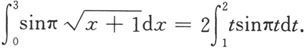
应用分部积分公式得
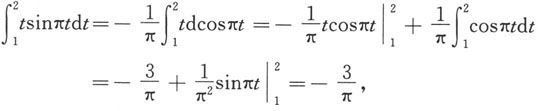
因此
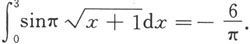
例5.3.9 计算定积分
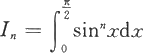 (n为正整数).
(n为正整数).
解 显然
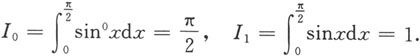
当n≥2时,利用分部积分法得
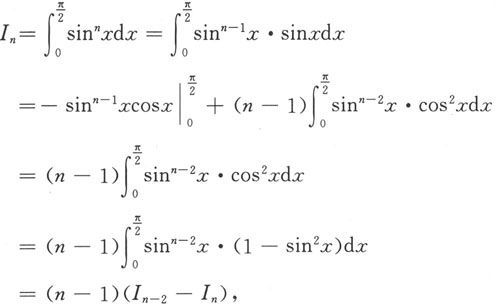
于是得到递推关系
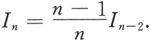
从这个递推关系得
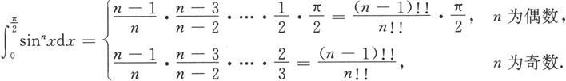
例5.3.10 计算定积分
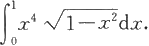
解 作变量代换x=sint得
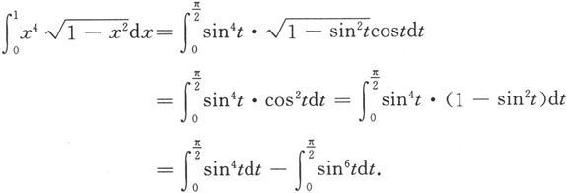
由例5.3.9知
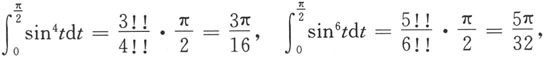
所以