





在本书第33节里我们提到(x+a)(x-a)=x 2 -a 2 ,将这个展开公式反过来看(从右往左)可得:x 2 -a 2 =(x+a)(x-a)。
这个式子展示了两个平方数相减时的因式分解。
利用这个公式我们可以很快地计算标题中的算式:
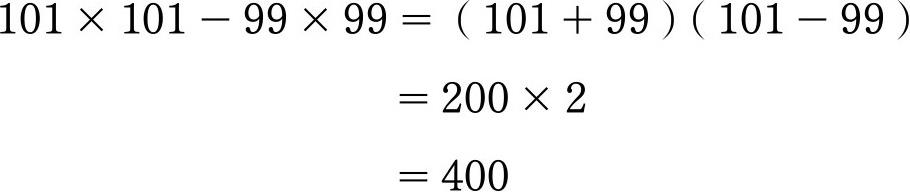
在实际的数学问题中,这种两个平方数相减的形式很常见,具有很高的利用价值。
例如,在右图中,直角三角形的斜边长为42厘米,一条直角边长为38厘米。
根据勾股定理(直角三角形中,斜边的平方等于其余两边的平方和),则图中x的长度的平方为:42×42-38×38。运用心算则可以快速得出:
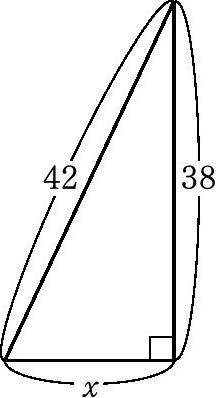
42×42-38×38=(42+38)(42-38)=80×4
举一个特别的例子,请计算:
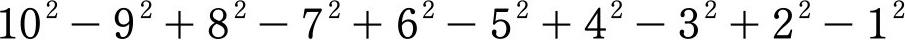
从首项开始两两组合,可将算式转化为两个平方数相减的形式,如第一项为:(10-9)(10+9)=10+9。
这道题的计算结果就是10+9+8+7+6+5+4+3+2+1。根据等差数列求和公式(本书第27节)计算可得:(10+1)×10÷2=55。
27×27-13×13=
74×74-71×71=
25×25-24×24+23×23-22×22=
2009×2009-2007×2007-209×209+207×207=
66×66-33×33=

相较于其他学科,数学里“需要记忆”的内容并不多。即使是公式,也是“推导”重于“背诵”,即“思考方式”重于“具体知识”。
不过,为了“掌握这些思考方式”,我们仍然离不开一些必要的知识。
以下,我们列举了若干“心算的常识”数字。不过这些数字即使我们不特地加以背诵,熟练之后也可以自然而然记住。
(1)11~19的平方数:
11 2 =121,12 2 =144,13 2 =169,14 2 =196,15 2 =225,16 2 =256,17 2 =289,18 2 =324,19 2 =361
(2)2的乘方:
2→4→8→16→32→64→128→256→512→1024
2 10 =1024,这个数字接近1000,最好加以记忆。
(3)乘法的分解:
91=7×13,108=3×36,111=3×37,
216=6×6×6,343=7×7×7,1001=7×11×13
这些数字经常出现,但我们往往不太留意。
最后,分数计算中4、6、8、9、12、18这些数字经常出现在分母位置,我们最好熟练记忆它们的通分。