




数对是一种特别的结构。什么是数对呢?我们通过一则示例来理解它。
1.隐性数对
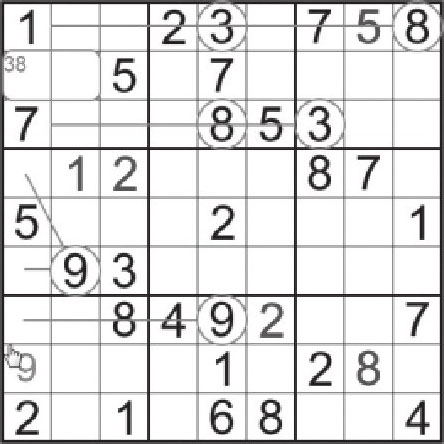
如图所示,我们可以直接观察到,数字3和数字8在第1宫的填数情况都只有同样的两格:B12。我们可以通过旁边的一簇3和8的提示数的排除,发现这一点。
因为3和8这两个数字都恰好只能填入到B12两格之中,所以这两格一定是3和8,别无其他。
观察第1列,数字9的填数位置就只剩下H1。所以H1是9。
这个技巧称为隐性数对,因为数对的存在是“隐性”的,它需要提示数做出排除后才会发现,它是隐藏在盘面之中的。而这里的3和8,我们可以说,它们是一个数对。
2.显性数对
有隐性数对,就有显性数对。

如图所示,观察第9列,发现C9只可能填入数字6和8;而恰好,同位于第9列的F9,也只可能填入6和8。所以,CF9这两格的填数只能是“此6彼8”或“此8彼6”的状态。但不论是哪种情况,因为6和8被确定下来在CF9两格,所以第9列其余位置肯定都不会是6和8了。否则,一定会有一个数和这两格的填数有重复。
随即观察第9宫。发现根据如此得到的结论后,数字6只能填入到H7,所以H7一定填6。
这个技巧称为显性数对,因为数对是直接裸露存在的,通过唯一余数类似的数数方式,就可以直接看到它们。
说起来简单,但使用起来可没有那么简单。所以以后还需要多加练习,巩固这些数独技巧。这些技巧也就是数独里最为基础的技巧,不论是在标准数独题还是变形数独题中,这些技巧都是存在的。