




1.因子(Factors or divisors)
定义:A number is a factor,or divisor,of another number if it can be divided evenly into that number.
例: What are the factors of 60?
解: 60=1×60=2×30=3×20=4×15=5×12=6×10,
所以60有1,2,3,4,5,6,10,12,15,20,30,60一共12个因子。
2.质因子(Prime factors)
定义:如果一个质数是某个数的约数,那么就说这个质数是某个数的质因数,也称质因子。
例:60=1×60=2×30=3×20=4×15=5×12=6×10,
60有12个因子,因子中2,3,5是质数,那么60的质因子便是2,3,5。
3.分解质因数
定义:把一个合数用质因子相乘的形式表示出来,叫作分解质因数。
例如:把60分解质因数。
60=2 2 ×3×5,其中2、3、5是60的质因子。
任何一个大于1的正整数,无论是质数还是合数都可以表示成质数因子相乘的形式。
例如:2=2 1 ,9=3 2 ,363=3×11 2 。
4.求任意一个自然数的因子个数
如何求任意一个自然数的因子个数呢?绝不是我们想象的那样硬着头皮去数,而是有公式可寻:
第一步:把该自然数分解质因数,即写成质数因子相乘的形式;
第二步:质因数分解式中每个质因子的指数加1相乘,这个连乘积便是所求因子数。
例: 120的因子个数是多少?
解: 120=2 3 ×3 1 ×5 1
那么120的因子的个数是(3+1)×(1+1)×(1+1)=16。
Example 1:
How many positive integers n are there such that 30n is a divisor of (2 3 )·(3)·(5 3 )?
(A)8
(B)6
(C)18
(D)9
(E)None
解: (2 3 )·(3)·(5 3 )=30×2 2 ×5 2
要使30n是(2 3 )×(3)×(5 3 )的因子,那么n就必须是2 2 ×5 2 的因子,2 2 ×5 2 有多少个不同的因子呢?利用因子个数的求法,共有(2+1)×(2+1)=9个,所以(D)是正确答案。
Example 2:
What is the smallest positive integer k for which 784 is a factor of 14 k ?
(A)6
(B)8
(C)4
(D)5
(E)10
解: 784=2 4 ×7 2 ,14 k =2 k ×7 k
要使784是14 k 的一个因子,那么14 k 就至少需要有4个质因子2,2个质因子7,因此k最少需要为4,选择(C)。
5.完全平方数的因子
定义:如果一个整数开平方之后还是整数,则这个数称之为完全平方数(perfect square)。
我们来观察一下,把一个完全平方数分解质因数后各质因子的指数有什么特征呢?
9=3 2
36=2 2 ×3 2
144=3 2 ×2 4
1600=2 6 ×5 2
275625=3 2 ×5 4 ×7 2
从上面我们可以看出,一个完全平方数分解质因数后,各质因子的指数均是偶数。我们可以从因子个数的计算公式中得到:
①一个完全平方数的因子个数必然为奇数。
②反之,任何一个自然数若它有奇数个因子,这个自然数必为完全平方数,若它有偶数个因子,则此自然数一定不是完全平方数。
例: 9=3 2 ,有2+1=3个因子,9是完全平方数。
30=2×3×5有(1+1)×(1+1)×(1+1)=8个因子,30不是完全平方数。
Example 3:
The product of a positive integer a and 1080 is a square number.What is the least value of a?
(A)4
(B)50
(C)60
(D)20
(E)30
解: 因为a与1080的乘积是一个完全平方数,那么乘积分解质因数后,各质因子的指数必然全部是偶数,1080×a=2 3 ×3 3 ×5×a,现在质因子2,3,5的个数都是奇数,那么a中必然含有质因子2、3、5,因此a最小为2×3×5=30,选择(E)。
Example 4:
Which of the following integers does NOT have a factor greater than 1 that is the square of an integer?
(A)100
(B)128
(C)72
(D)54
(E)42
解: 把选项中的数分解质因数后,如果每个质因子的指数都小于2,那么这个数便是答案。
100=2 2 ×5 2 ,128=8 2 ×2,72=2×6 2 ,前三个选项都有能够表达为完全平方数的因子。许多考生在第四个选项上犯了错误,认为54=2×3 3 ,没有因子能够表达为完全平方数。其实不然,54=2×3 3 ,那么32必然也是54的因子。这一点在GMAT的数据充分性题目中也曾经出现过,希望引起考生注意。选项(E)42=6×7,显然没有因子能够表达为完全平方数,所以选择(E)。
Example 5:
Is the positive integer m equal to the cube of an integer?
(1)For every prime number q,if q is a factor of m,then q 3 is also a divisor of m.
(2)
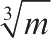 is an integer.
is an integer.
解: 单独(1),q,q 3 是m的因子,m不一定是完全立方数,比如m=q 4 同样能满足q,q 3 是m的因子。
单独(2),
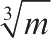 是整数,满足完全立方数的定义,所以选择(B)。
是整数,满足完全立方数的定义,所以选择(B)。
性质1
只有2个因子的自然数都是质数。
性质2
若自然数n不是完全平方数,则n的因子中小于
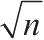 的因子占一半,大于
的因子占一半,大于
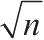 的因子也占一半。
的因子也占一半。
例:
60有多少个小于
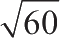 的因子?
的因子?
解: 60=2 2 ×3×5,那么60共有12个因子。
根据性质2,12/2=6,则60有6个小于
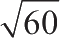 的因子。
的因子。
性质3
若自然数n是完全平方数,并且
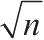 也是n的一个因子,那么在n的所有因子中除去
也是n的一个因子,那么在n的所有因子中除去
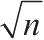 之外,小于
之外,小于
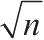 的因子占余下的一半,大于
的因子占余下的一半,大于
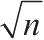 的因子也占余下的一半。
的因子也占余下的一半。
例:
64有多少小于
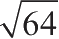 的因子?
的因子?
解:
64=2
6
,6+1=7,所以64有7个因子,由于
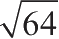 =8,也是64的一个因子,
=8,也是64的一个因子,
所以小于
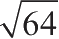 的因子为
的因子为
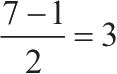 ;大于
;大于
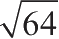 的因子,同理也为
的因子,同理也为
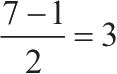 。
。
性质4
如果自然数n有m个因子,m为大于2的质数,那么n必为某一质数的(m-1)次方。
其实必然如此,自然数的因子个数为质因子的指数加1相乘,现在有m个因子,而m为大于2的质数,写成(指数+1)相乘的形式只能够为(m+1)。比如说5,5写成指数加1相乘的形式只能为(4+1),这也就说明了这个自然数的质因子个数只可能为1,质因子的指数为4。
例: 16=2 4 ,有4+1=5个因子,5为大于2的质数,16为质数2的(5-1)=4次方。
81=3 4 ,有4+1=5个因子,5为大于2的质数,81为质数3的(5-1)=4次方。
Example 1:
如果某一自然数除了1之外只有2个因子,则这个自然数必为:
(A)奇数
(B)偶数
(C)4的倍数
(D)某一质数的平方
(E)质数
解: 既然这个数除了1之外只有2个因子,则这个数一共有3个因子(把因子1加上),而3是一个大于2的质数,根据性质4得到它必然是某一质数的3-12次方,所以(D)为正确答案。
许多同学做这道题目时代入数字进行排除也能够很快做出来,不能说不对,但是知道了一些性质,在数字大的时候就好办多了。
Example 2:
k and s are two positive integers such that k>s,if k×s=132,what is the total number of possible values of k?
(A)4
(B)6
(C)7
(D)8
(E)10
解:
k×s=132,那么k,s必然是132的因子,由于k和s满足k>s,因此k必然是大于
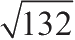 的因子,s必然是小于
的因子,s必然是小于
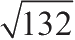 的因子。这道题目转化为132有多少个因子大于
的因子。这道题目转化为132有多少个因子大于
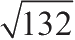 ,132=2
2
×3×11,共有3×2×212个因子,利用性质2得到有12/2=6个因子大于
,132=2
2
×3×11,共有3×2×212个因子,利用性质2得到有12/2=6个因子大于
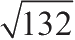 ,所以(B)是正确答案。
,所以(B)是正确答案。